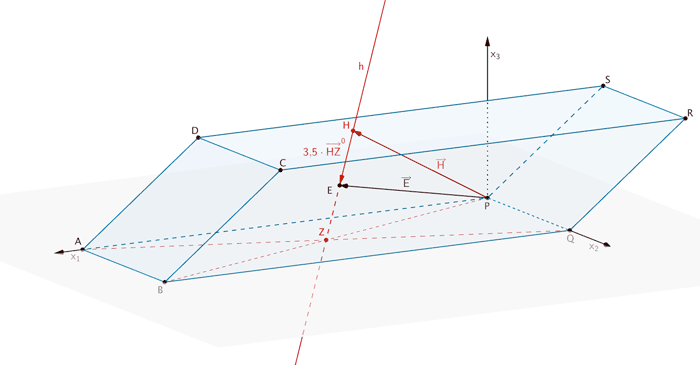
Der Grundkörper ist mit einer dünnen geradlinigen Bohrung versehen, die im Modell vom Punkt \(H\,(11|3|6)\) der Deckfläche \(DCRS\) aus in Richtung des Schnittpunkts der Diagonalen der Grundfläche verläuft. In der Bohrung ist eine gerade Stahlstange mit einer Länge von 1,4 m so befestigt, dass die Stange zu drei Vierteln ihrer Länge aus der Deckfläche herausragt.

Bestimmen Sie im Modell eine Gleichung der Geraden \(h\), entlang derer die Bohrung verläuft, sowie die Koordinaten des Punkts, in dem die Stange in der Bohrung endet.

(zur Kontrolle: möglicher Richtungsvektor von \(h\): \(\displaystyle \begin{pmatrix} 3 \\ 2 \\ -6 \end{pmatrix}\))

(7 BE)

Lösung zu Teilaufgabe g

\[H\,(11|3|6) \quad H \in DCRS\]

Gleichung der Geraden \(h\)

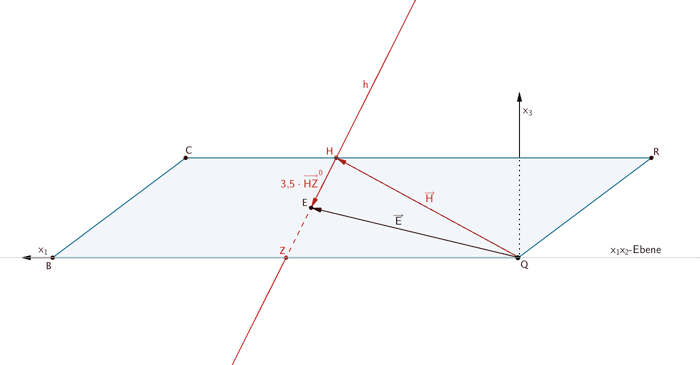
Gerade \(h\) durch den Punkt \(H\) und den Mittelpunkt der Diagonalen \([AQ]\) und \([BP]\) der Grundfläche \(ABQP\) des Spats

Es sei \(H\) der Aufpunkt der Geraden \(h\) und \(Z\) der Mittelpunkt der Diagonalen \([AQ]\) und \([BP]\).

\[h\,\colon\; \overrightarrow{X} = \overrightarrow{H} + \lambda \cdot \overrightarrow{HZ}\]

Mittelpunkt \(Z\) der Diagonalen \([AQ]\) und \([BP]\) berechnen:

\[B\,(28|10|0), \enspace P\,(0|0|0)\]

\[\overrightarrow{Z} = \frac{1}{2} \cdot \left(\overrightarrow{B} + \overrightarrow{P}\right) = \frac{1}{2} \cdot \overrightarrow{B} = \frac{1}{2} \cdot \begin{pmatrix} 28 \\ 10 \\ 0 \end{pmatrix} = \begin{pmatrix} 14 \\ 5 \\ 0 \end{pmatrix}\]

Richtungsvektor \(\overrightarrow{HZ}\) der Geraden \(h\) berechnen:

\[\overrightarrow{HZ} = \overrightarrow{Z} - \overrightarrow{H} = \begin{pmatrix} 14 \\ 5 \\ 0 \end{pmatrix} - \begin{pmatrix} 11 \\ 3 \\ 6 \end{pmatrix} = \begin{pmatrix} 3 \\ 2 \\ -6 \end{pmatrix}\]

\[\Longrightarrow \quad h\,\colon\; \overrightarrow{X} = \begin{pmatrix} 11 \\ 3 \\ 6 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 3 \\ 2 \\ -6 \end{pmatrix}\]

Koordinaten des Punkts, in dem die Stange in der Bohrung endet

Länge der Stahlstange: 1,4 m

Die Stahlstange ragt zu drei Vierteln aus der Deckfläche heraus, d.h. sie reicht zu einem Viertel in die Bohrung hinein.

\[\frac{1}{4} \cdot 1{,}4\,\text{m} = \frac{7}{20}\,\text{m} = 0{,}35\,\text{m}\]

\[0{,}1\,\text{m} \,\mathrel{\widehat{=}} \, 1\,\text{LE} \quad \Longrightarrow \quad 0{,}35\,\text{m} \mathrel{\widehat{=}} \, 3{,}5\,\text{LE}\]

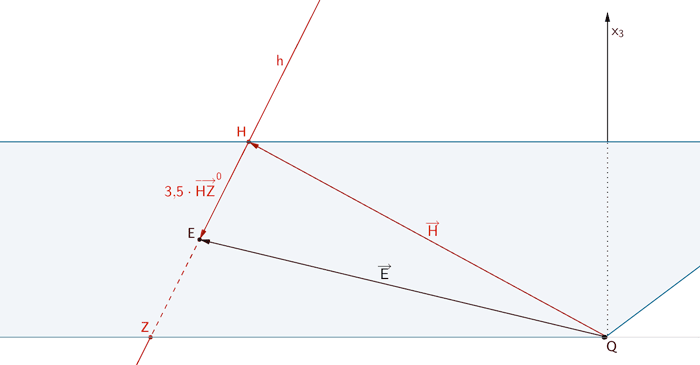
Es sei \(E\) der Punkt in dem die Stahlstange in der Bohrung endet.

\[\overline{HE} = 3{,}5\,\text{LE}\]

1.Lösungsansatz: Einheitsvektor des Richtungsvektors der Geraden \(h\)

• 
• 
• 

Addiert man zum Ortsvektor \(\overrightarrow{H}\) das 3,5-fache des Einheitsvektors \(\overrightarrow{HZ}^0\) des Richtungsvektors \(\overrightarrow{HZ}\) der Geraden \(h\), so erhält man den Ortsvektor \(\overrightarrow{E}\).

\[\overrightarrow{E} = \overrightarrow{H} + 3{,}5 \cdot \overrightarrow{HZ}^0\]

Einheitsvektor \(\overrightarrow{HZ}^0\) berechnen:

\[\overrightarrow{HZ}^0 = \frac{\overrightarrow{HZ}}{\vert \overrightarrow{HZ} \vert} = \frac{\begin{pmatrix} 3 \\ 2 \\ -6 \end{pmatrix}}{\sqrt{3^2 + 2^2 + (-6)^2}} = \frac{1}{7} \cdot \begin{pmatrix} 3 \\ 2 \\ -6 \end{pmatrix}\]

Koordinaten des Punktes \(E\) berechnen:

\[\begin{align*} \overrightarrow{E} &= \overrightarrow{H} + 3{,}5 \cdot \overrightarrow{HZ}^0 \\[0.8em] &= \begin{pmatrix} 11 \\ 3 \\ 6 \end{pmatrix} + 3{,}5 \cdot \frac{1}{7} \cdot \begin{pmatrix} 3 \\ 2 \\ -6 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 11 \\ 3 \\ 6 \end{pmatrix} \frac{1}{2} \cdot \begin{pmatrix} 3 \\ 2 \\ -6 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 12{,}5 \\ 4 \\ 3 \end{pmatrix} \end{align*}\]

\[\Longrightarrow \quad E\,(12{,}5|4|3)\]

2.Lösungsansatz: Länge einer Strecke entlang einer Geraden

\[\overline{HE} = 3{,}5\,\text{LE}\]

\[E \in h\,; \quad h\,\colon\; \overrightarrow{X} = \begin{pmatrix} 11 \\ 3 \\ 6 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 3 \\ 2 \\ -6 \end{pmatrix}\]

Der Ortsvektor \(\overrightarrow{E}\) lässt sich in Abhängigkeit des Parameters \(\lambda\) der Geradengleichung von \(h\) formulieren.

\[\overrightarrow{E}(\lambda) = \begin{pmatrix} 11 + 3\lambda \\ 3 + 2\lambda \\ 6 - 6\lambda \end{pmatrix}\]

Länge der Strecke \([HE]\) in Abhängigkeit des Parametres \(\lambda\) beschreiben:

\[\begin{align*} \overline{HE}(\lambda) &= \vert \overrightarrow{HE}(\lambda) \vert \\[0.8em] &= \vert \overrightarrow{E}(\lambda) - \overrightarrow{H} \vert \\[0.8em] &= \left| \begin{pmatrix} 11 + 3\lambda \\ 3 + 2\lambda \\ 6 - 6\lambda \end{pmatrix} - \begin{pmatrix} 11 \\ 3 \\ 6 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} 3\lambda \\ 2\lambda \\ -6\lambda \end{pmatrix} \right| \\[0.8em] &= \sqrt{(3\lambda)^2 + (2\lambda)^2 + (-6\lambda)^2} \\[0.8em] &= \sqrt{9\lambda^2 + 4\lambda^2 + 36\lambda^2} \\[0.8em] &= \sqrt{49\lambda^2} \\[0.8em] &= \pm 7\lambda \end{align*}\]

Parameterwerte für \(\lambda\) bestimmen:

\[\overline{HE}(\lambda) = 3{,}5\]

\[\begin{align*} 7\lambda &= 3{,}5 & &| : 7 & &\vee & -7\lambda &= 3{,}5 & &| : (-7) \\[0.8em] \lambda &= \frac{1}{2} & & & & & \lambda &= -\frac{1}{2}   \end{align*}\]

Parameterwerte \(\displaystyle \lambda = \pm \frac{1}{2}\) in \(\overrightarrow{E}(\lambda)\) einsetzen:

\[\overrightarrow{E}(\lambda) = \begin{pmatrix} 11 + 3\lambda \\ 3 + 2\lambda \\ 6 - 6\lambda \end{pmatrix}\]

\[\overrightarrow{E}_1 = \begin{pmatrix} 11 + 3 \cdot \frac{1}{2} \\ 3 + 2 \cdot \frac{1}{2} \\ 6 - 6 \cdot \frac{1}{2} \end{pmatrix} = \begin{pmatrix} 12{,}5 \\ 4 \\ 3 \end{pmatrix}\]

\[\Longrightarrow \quad E_1\,(12{,}5|4|3)\]

\[\overrightarrow{E}_2 = \begin{pmatrix} 11 + 3 \cdot \left(-\frac{1}{2}\right) \\ 3 + 2 \cdot \left(-\frac{1}{2}\right) \\ 6 - 6 \cdot \left(-\frac{1}{2}\right) \end{pmatrix} = \begin{pmatrix} 9{,}5 \\ 2 \\ 9 \end{pmatrix}\]

\[\Longrightarrow \quad E_2\,(9{,}5|2|9)\]

Der Punkt \(E_2\) kommt nicht in Frage, da er mit \(x_{3_{E_2}} = 9\) höher als der Punkt \(H\,(11|3|6)\) liegt. Der gesuchte Punkt ist \(E_1\,(12{,}5|4|3)\).