Vor einer Schule stehen zehn Fahrräder nebeneinander; zwei davon sind Mountainbikes. Bestimmen Sie die Wahrscheinlichkeit dafür, dass die beiden Mountainbikes unmittelbar nebeneinander stehen, wenn die Anordnung der Fahrräder zufällig erfolgte.
(3 BE)
Lösung zu Teilaufgabe 3
Laplace-Wahrscheinlichkeit
Laplace-Wahrscheinlichkeit eines Ereignisses \(A\)
\[P(A) = \frac{\vert A \vert}{\vert \Omega \vert} = \frac{\text{Anzahl der für} \; A \; \text{günstigen Ergebnisse}}{\text{Anzahl der möglichen Ergebnisse}}\]
Voraussetzung: Alle Ergebnisse (alle Versuchsausgänge) des betrachteten Zufallsexperiments sind gleichwahrscheinlich (Laplace-Experiment).
Anzahl der Möglichkeiten, zwei Mountainbikes von insgesamt zehn nebeneinander stehenden Fahrrädern abzustellen:
Binomialkoeffizient
Der Binomialkoeffizient gibt an, wie viele Möglichkeiten es gibt, aus einer Menge mit \(n\) Elementen eine Teilmenge mit \(k\) Elementen zu bilden.
\[\binom{n}{k} = \frac{n!}{k! \cdot (n - k)!} = \frac{n \cdot (n - 1) \cdot ... \cdot (n - k + 1)}{k!}\]
(vgl. Merkhilfe)
Es gibt \(\displaystyle \binom{10}{2}\) Möglichkeiten, zwei Mountainbikes von insgesamt zehn nebeneinander stehenden Fahrrädern abzustellen.
Anzahl der Möglichkeiten, zwei Mountainbikes von insgesamt zehn nebeneinander stehenden Fahrrädern nebeneinander abzustellen:
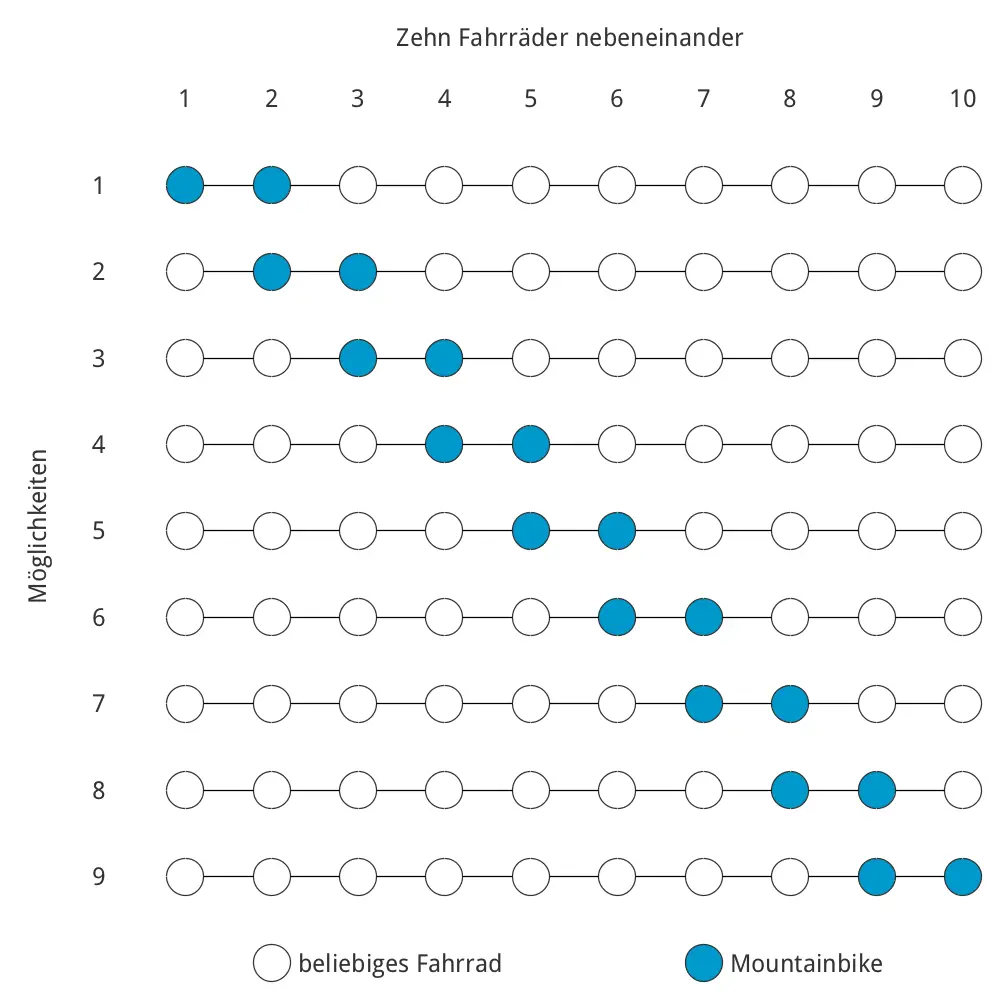
Es gibt neun Möglichkeiten, zwei Mountainbikes von insgesamt zehn nebeneinander stehenden Fahrrädern nebeneinander abzustellen.
Anmerkung: Für \(n \geq k\) gibt es \(n - k +1\) Möglichkeiten, eine Teilmenge von \(k\) Objekten nebeneinander und ohne Berücksichtigung deren Reihenfolge (ohne Unterscheidung) auf \(n\) Objekte zu verteilen.
Laplace-Wahrscheinlichkeit berechnen:
Binomialkoeffizient
Der Binomialkoeffizient gibt an, wie viele Möglichkeiten es gibt, aus einer Menge mit \(n\) Elementen eine Teilmenge mit \(k\) Elementen zu bilden.
\[\binom{n}{k} = \frac{n!}{k! \cdot (n - k)!} = \frac{n \cdot (n - 1) \cdot ... \cdot (n - k + 1)}{k!}\]
(vgl. Merkhilfe)
\[\begin{align*}P(\text{ „MTBs nebeneinander"}) &= \frac{9}{\binom{10}{2}} \\[0.8em] &= \frac{9}{\frac{10!}{2! \cdot (10 - 2)!}} \\[0.8em] &= \frac{9}{\frac{\cancel{1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdot 7 \cdot 8} \cdot 9 \cdot 10}{1 \cdot 2 \; \cdot \; \cancel{1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdot 7 \cdot 8}}} \\[0.8em] &= \frac{9}{\frac{9 \cdot 10}{1 \cdot 2}} \\[0.8em] &= \frac{9}{45} = \frac{1}{5} = 20\,\% \end{align*}\]

