Eine Funktion \(f\) mit \(f(x) = mx + t\) und \(m,t \in \mathbb R\) heißt lineare Funktion. Dabei ist \(m\) die Steigung der Funktion und \(t\) der \(y\)-Achsenabschnitt.
Definitionsmenge: \(D_{f} = \mathbb R\)
Wertemenge (für \(m \neq 0\)): \(W_{f} = \mathbb R\)
Eine lineare Funktion besitzt für \(m \neq 0\) genau eine Nullstelle: \(x = -\frac{t}{m}\).
Funktionsgraph einer linearen Funktion
Der Funktionsgrapph einer linearen Funktion ist eine Gerade.
\(m < 0 \colon \quad\) Die Gerade ist steigend.
\(m = 0 \colon \quad\) Die Gerade verläuft horizontal (parallel zur \(x\)-Achse)
\(m < 0 \colon \quad\) Die Gerade ist fallend
Steigung \(m\) und Steigungswinkel \(\alpha\) einer Gerade
Zwei beliebige Punkte \(P_{1}(x_{1}|y_{1})\) und \(P_{2}(x_{2}|y_{2})\) mit \(x_{1} \neq x_{2}\) legen eine Gerade eindeutig fest. Ebenso ist eine Gerade durch die Angabe eines ihrer Punkte und ihrer Steigung eindeutig bestimmt.
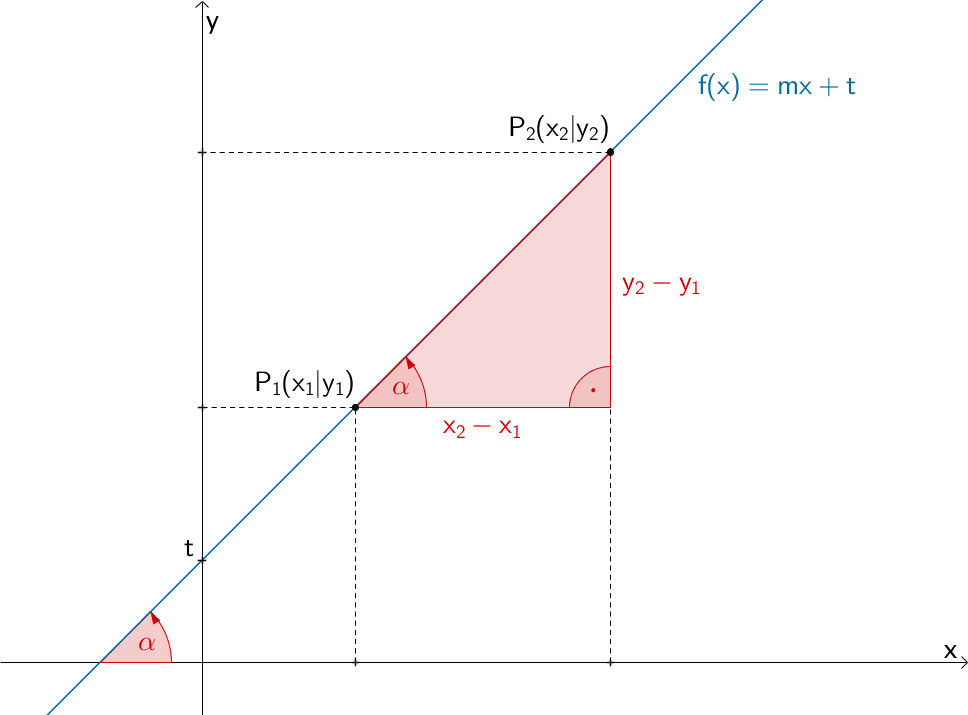
Gerade mit Steigungsdreieck, Steigungswinkel \(\alpha\) und \(y\)-Achsenabschnitt \(t\)
Der Steigungswinkel einer Gerade ist der in mathematisch positivem Sinn (gegen den Uhrzeigersinn) gemessene Winkel, den die Gerade mit der positiven \(x\)-Achse einschließt.
Steigung \(\boldsymbol{m}\) einer Gerade
\[m = \frac{\Delta y}{\Delta x} = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}\]
Steigungswinkel \(\boldsymbol{\alpha}\) einer Gerade
\[\tan{\alpha} = m \enspace (\alpha \neq 90^{\circ})\]
Parallele und senkrechte (orthogonale) Geraden
Zwei Geraden \(g_{1}\) und \(g_{2}\) sind
parallel zueinander, wenn
\[m_{1} = m_{2}\]
gilt.
senkrecht zueinander, wenn
\[m_{1} \cdot m_{2} = -1\]
gilt.
Geradengleichungen
Neben der allgemeinen Form, lässt sich die Gleichung einer Gerade in der Ebene, die durch den Punkt \((x_{0}|y_{0})\) verläuft und die Steigung \(m\) besitzt, in der Punkt-Steigungs-Form formulieren.
Allgemeine Form einer Gerade
\[y = mx + t\]
Punkt-Steigung-Form einer Gerade
\[y = m (x - x_{0}) + y_{0}\]
Beispielaufgabe
Die Gerade \(g\) verläuft durch die Punkte \(A(2|3)\) und \(B(6|5)\). Ermitteln Sie die Gleichung der Gerade \(g\) in der allgemeinen Form und in der Punkt-Steigung-Form. Berechnen Sie den Steigungswinkel \(\alpha\) der Gerade \(g\). Ermitteln Sie eine Gleichung der Gerade \(h\), welche im Punkt \(A\) senkrecht zur Gerade \(g\) verläuft.
Steigung \(m\) berechnen:
\[A(2|3)\,, \enspace B(6|5)\]
\[m =\frac{y_{B} - y_{A}}{x_{B} - x_{A}} = \frac{5 - 3}{6 - 2} = \frac{2}{4} = \frac{1}{2}\]
Geradengleichung von \(g\) in der allgemeinen Form:
\[\begin{align*} g \colon y &= mx + t \\[0.8em] y &= \frac{1}{2}x + t \\[0.8em] \end{align*}\]
\[\begin{align*}A \in g \colon 3 &= \frac{1}{2} \cdot 2 + t \\[0.8em] 3 &= 1 + t & &| -1 \\[0.8em] 2 &= t \end{align*}\]
\[\Longrightarrow \quad g \colon y = \frac{1}{2}x + 2\]
Geradengleichung von \(g\) in der Punkt-Steigungs-Form:
\[A(2|3)\,, \enspace B(6|5)\,, \enspace m = \dfrac{1}{2}\]
Da zwei Punkte der Gerade \(g\) bekannt sind, gibt es zwei Möglichkeiten, eine Geradengleichung in der Punkt-Steigungs-Form anzugeben.
\[\begin{align*} g \colon y &= m(x - x_{A}) + y_{A} \\[0.8em] y &= \frac{1}{2} (x - 2) + 3 \end{align*}\]
\[\begin{align*} g \colon y &= m(x - x_{B}) + y_{B} \\[0.8em] y &= \frac{1}{2} (x - 6) + 5 \end{align*}\]
Steigungswinkel \(\alpha\) der Gerade \(g\):
\[\begin{align*} \tan{\alpha} &= m \\[0.8em] \tan{\alpha} &= \frac{1}{2} & &| \; \tan^{-1}(\dots) \; \text{(TR: SHIFT + tan)} \\[3.2em] \alpha &\approx 26{,}57^{\circ} \end{align*}\]
Gleichung der Gerade \(h\):
\[h \perp g\,, \enspace A(2|3) \in h\,, \enspace m_{g} = \dfrac{1}{2}\]
\[\begin{align*} m_{g} \cdot m_{h} &= -1 & &| : m_{g} \\[0.8em] m_{h} &= -\frac{1}{m_{g}} \\[0.8em] &= -\frac{1}{\frac{1}{2}} \\[0.8em] &= -2 \end{align*}\]
\[\begin{align*}h \colon y &= m_{h}x + t \\[0.8em] y &= -2x + t \end{align*}\]
\[\begin{align*}A \in h \colon 3 &= -2 \cdot 2 + t \\[0.8em] 3 &= -4 + t & &| + 4 \\[0.8em] 7 &= t \end{align*}\]
\[\Longrightarrow \quad h \colon y = -2x + 7\]
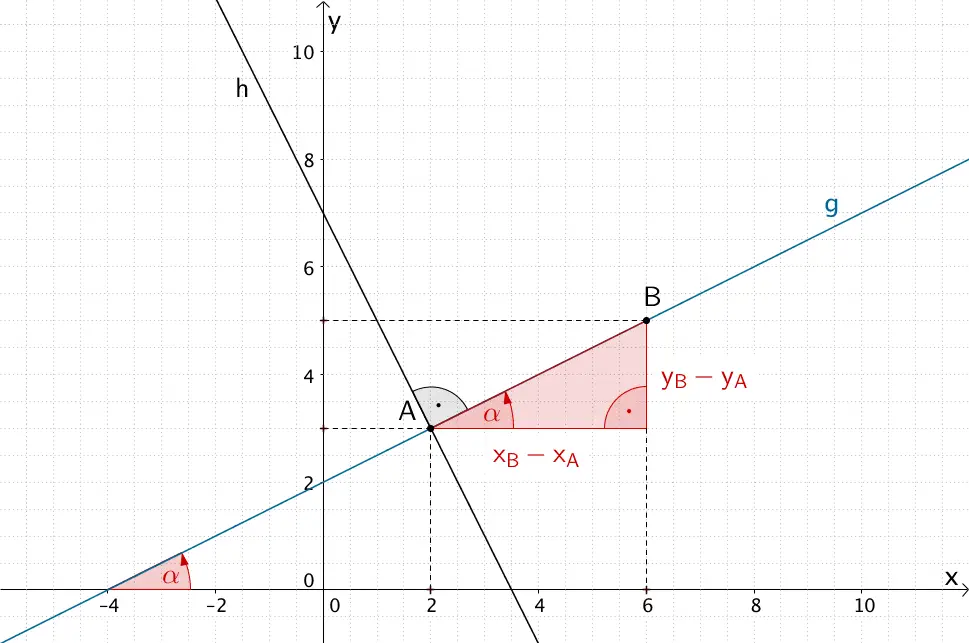
Gerdade \(g\) mit Steigungswinkel \(\alpha\) und senkrechte Gerade \(h\)

