Eine Funktion \(f\) mit \(f(x) = a_{n}x^{n} + a_{n-1}x^{n-1} + \textstyle{\dots} + a_{1}x + a_{0}\) und \(n \in \mathbb N_{0}\) sowie den Koeffizienten \(a_{i} \in \mathbb R, a_{n} \neq 0\) heißt ganzrationale Funktion oder Polynomfunktion vom Grad \(n\).
Definitionsmenge: \(D_{f} = \mathbb R\)
Ganzrationale Funktionen vom Grad 0 sind konstante Funktionen (z.B. \(f(x) = 3\)).
Ganzrationale Funktionen vom Grad 1 sind lineare Funktionen (z.B. \(f(x) = 2x + 3\), vgl. Abiturskript - 1.1.1 Lineare Funktion).
Ganzrationale Funktionen vom Grad 2 sind quadratische Funktionen (z.B. \(3x^{2} - 4x + 5\), vgl. Abiturskript - 1.1.2 Quadratische Funktion).
Zu den ganzrationalen Funktionen gehören auch die Potenzfunktionen mit \(f(x) = x^{n}\) und \(n \in \mathbb N\).
Nullstellen einer ganzrationalen Funktion
Die Nullstellen einer ganzrationalen Funktion höheren Grades lassen sich häufig nur noch näherungsweise oder durch Probieren ermitteln.
Nullstelle durch Probieren finden: Sind alle Koeffizienten \(a_{n} \dots a_{0}\) einer ganzrationalen Funktion ganzzahlig, kommen als ganzzahlige Nullstellen nur ganzzahlige Teiler von \(a_{0}\) in Frage.
Eine ganzrationale Funktion von Grad \(\boldsymbol{n}\) besitzt höchstens \(\boldsymbol{n}\) Nullstellen. Sie kann auch keine Nullstelle oder eine Nullstelle vielfach (doppelt, dreifach ...) besitzen.
Vielfachheit von Nullstellen ganzrationaler Funktionen
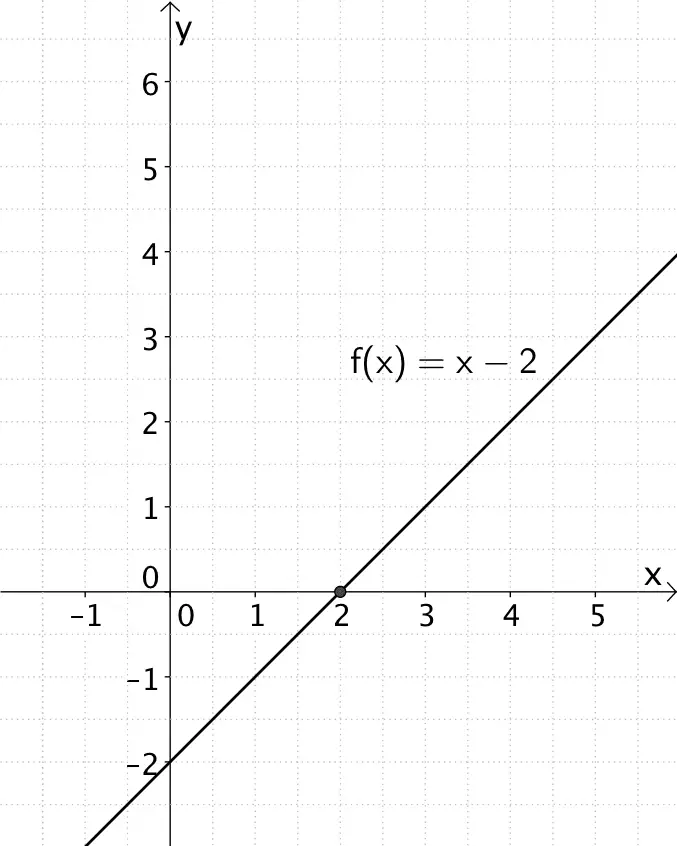
Einfache Nullstelle mit Vorzeichenwechsel
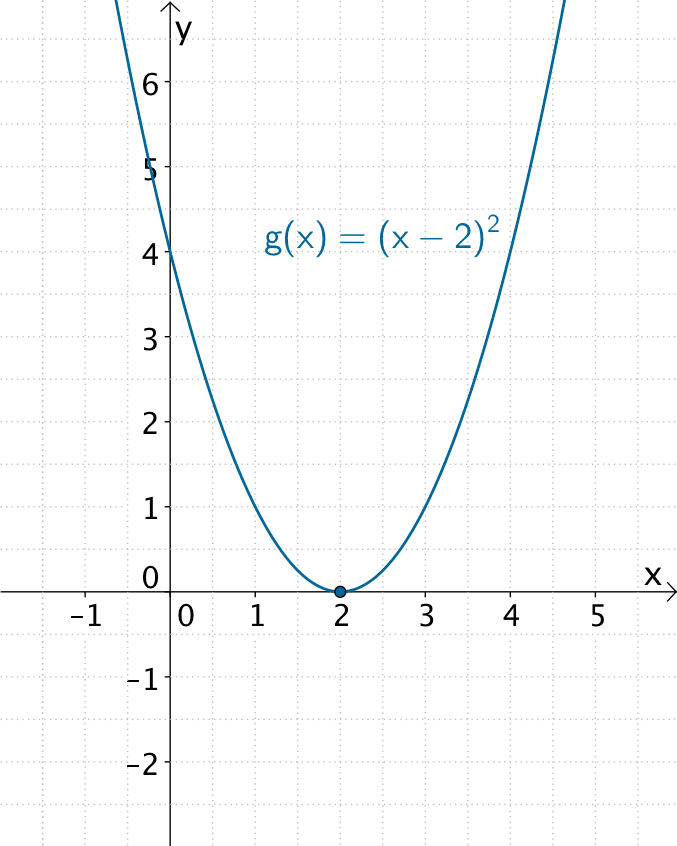
Doppelte Nullstelle ohne Vorzeichenwechsel
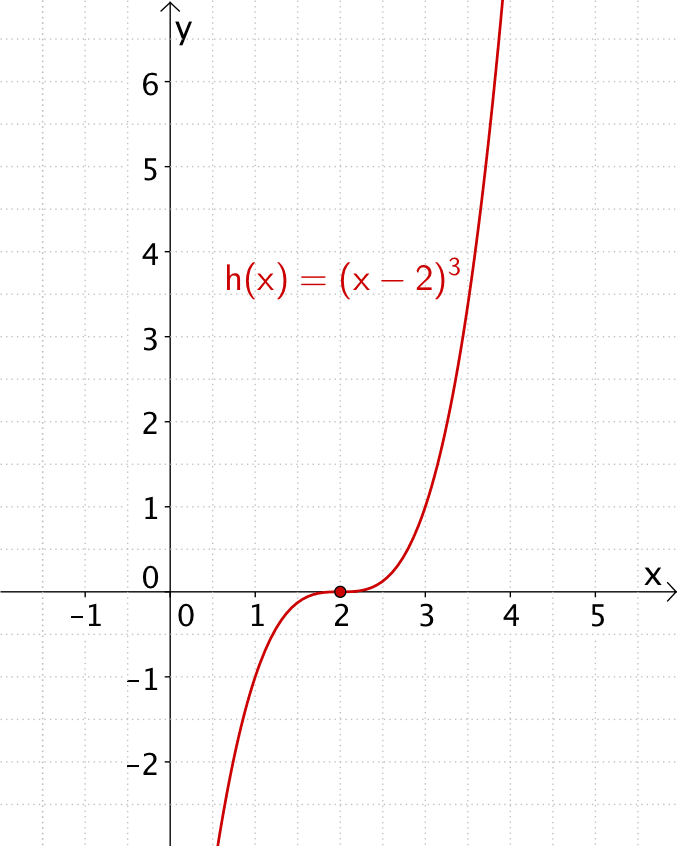
Dreifache Nullstelle mit Vorzeichenwechsel
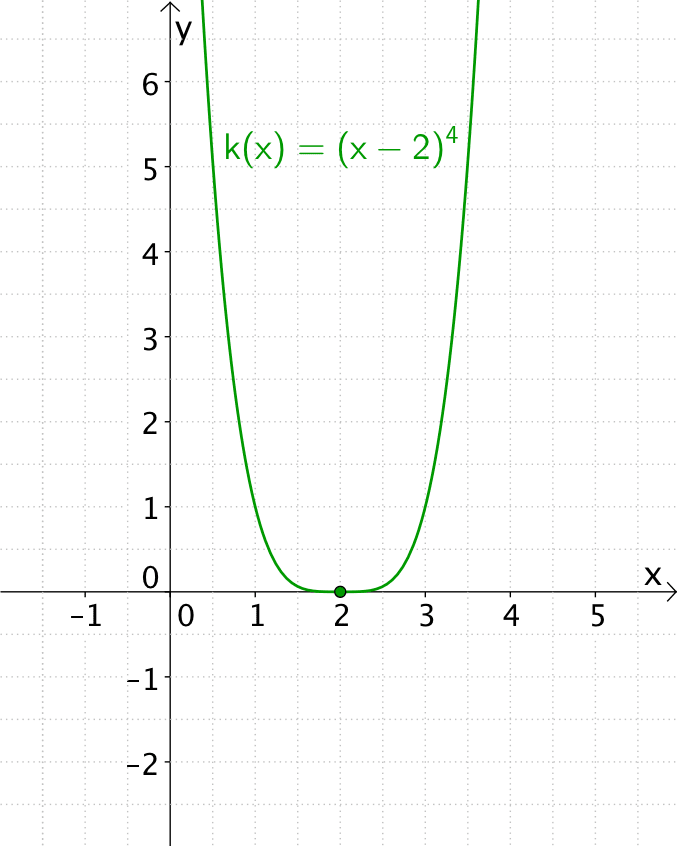
Vierfache Nullstelle ohne Vorzeichenwechsel
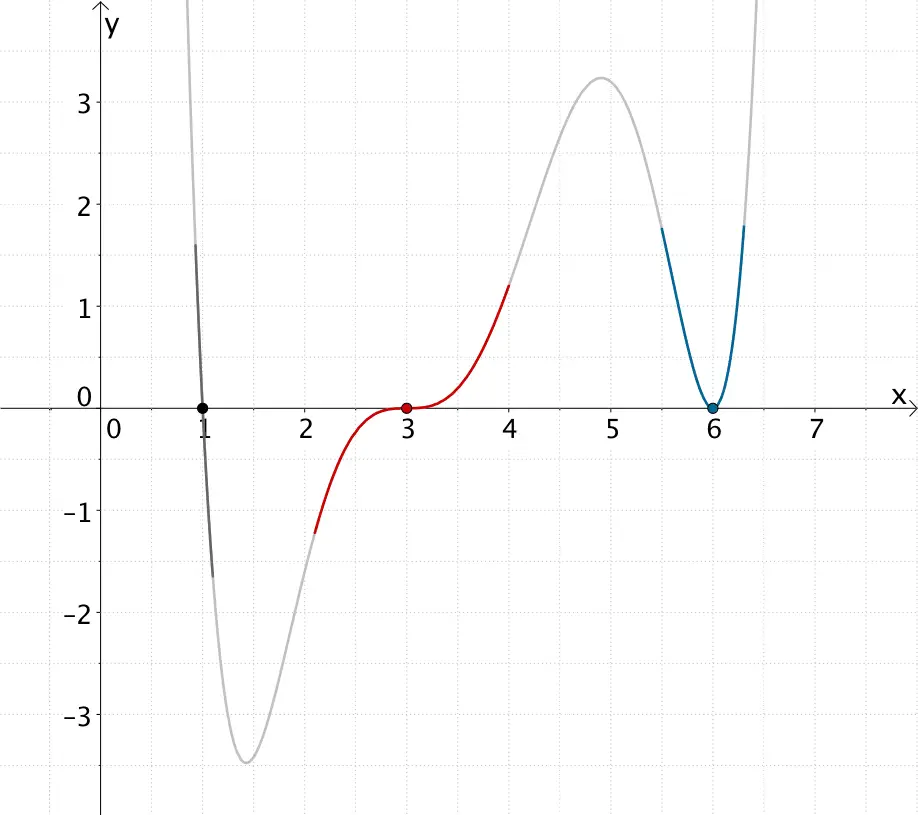
Graph der ganzrationalen Funktion \(f\colon x \mapsto 0{,}1(x - 1)(x - 3)^{3}(x - 6)^{2}\) mit der einfachen Nullstelle \(x = 1\), der dreifachen Nullstelle \(x = 3\) und der doppelten Nullstelle \(x = 6\)
Nullstellen ungerader Ordnung
Eine ganzrationale Funktion \(f\) hat an der Stelle \(x_{0}\) eine Nullstelle ungerader Ordnung, wenn der zugehörige Linearfaktor \(x - x_{0}\) der Funktion \(f\) in ungerader Potenz auftritt. Der Graph von \(f\) weist dann an der Nullstelle \(x_{0}\) einen Vorzeichenwechsel auf.
Nullstellen gerader Ordnung
Eine ganzrationale Funktion \(f\) hat an der Stelle \(x_{0}\) eine Nullstelle gerader Ordnung, wenn der zugehörige Linearfaktor \(x - x_{0}\) der Funktion \(f\) in gerader Potenz auftritt. Der Graph von \(f\) weist dann an der Nullstelle \(x_{0}\) keinen Vorzeichenwechsel auf.
Produktform und Linearfaktoren einer ganzrationalen Funktion
Sind die Nullstellen \(x_{1}, x_{2} ..., x_{n}\) einer ganzrationalen Funktion bekannt, lässt sich diese als Produkt ihrer Linearfaktoren \(x - x_{1}, x - x_{2}, \dots, x - x_{n}\) darstellen.
Produktform einer ganzrationalen Funktion
\[\begin{align*} f(x) &= a_{n}x^{n} + a_{n-1}x^{n-1} + \textstyle{\dots} + a_{1}x + a_{0} \\[0.8em] &= a_{n}(x - x_{1})(x - x_{2}) \dots (x - x_{n})\end{align*}\]
\(x_{1}, x_{2}, \textstyle{\dots}, x_{n}\): Nullstellen von \(f\)
\((x - x_{1}), (x - x_{2}), \textstyle{\dots}, (x - x_{n})\): Linearfaktoren von \(f\)
Vorgehensweise - Nullstellen einer ganzrationalen Funktion bestimmen
1. Beispiel
Bestimmen Sie die Nullstellen der in \(\mathbb R\) definierten Funktion \(f \colon x \mapsto 2x^{3} + 3x^{2} -2x\).
Da der Funktionsterm den konstanten Summanden \(a_{0}\) nicht enthält, lässt sich \(x\) ausklammern. Der Funktionsterm wird dadurch in ein Produkt umgewandelt.
\[\begin{align*} f(x) &= 0 \\[0.8em] \underbrace{2x^{3} + 3x^{2} - 2x}_{\text{Summe}} &= 0 &&| \; x \; \text{ausklammern} \\[0.8em] \underbrace{\underbrace{\textcolor{#cc071e}{x}}_{\textcolor{#cc071e}{\text{Faktor 1}}} \cdot \underbrace{\textcolor{#0087c1}{(2x^{2} + 3x - 2)}}_{\textcolor{#0087c1}{\text{Faktor 2}}}}_{\text{Produkt}} &= 0 \end{align*}\]
Satz vom Nullprodukt anwenden:
„Ein Produkt ist gleich Null, wenn einer der Faktoren gleich Null ist."
\[\Rightarrow \enspace \textcolor{#cc071e}{x_{1}} = 0 \enspace \vee \enspace \textcolor{#0087c1}{2x^{2} + 3x - 2} = 0\]
Lösungsformel für quadratische Gleichungen (Mitternachtsformel) anwenden (vgl. Abiturskript - 1.1.2 Quadratische Funktion):
\[x_{2,3} = \frac{-3 \pm \sqrt{3^{2} - 4 \cdot 2 \cdot (-2)}}{2 \cdot 2} = \frac{-3 \pm \sqrt{25}}{4} = \frac{-3 - 5}{4}\]
\[x_{2} = \frac{-3 - 5}{4} = \frac{-8}{4} = -2\]
\[x_{3} = \frac{-3 + 5}{4} = \frac{2}{4} = 0{,}5\]
Die Funktion \(f \colon x \mapsto 2x^{3} + 3x^{2} -2x\) besitzt die Nullstellen \(x = -2\), \(x = 0\) und \(x = 0{,}5\).
2. Beispiel
Bestimmen Sie die Nullstellen der in \(\mathbb R\) definierten Funktion \(f \colon x \mapsto x^{3} - 4x^{2} -x + 4\).
Da der Funktionsterm den konstanten Summanden \(a_{0} = 4\) enthält, ist das Ausklammern von \(\textcolor{#cc071e}{x}\) (oder einer höheren Potenz von \(x\)) zwar möglich, aber nicht zielführend.
\[\begin{align*}f(x) &= 0 \\[0.8em] x^{3} - 4x^{2} - x + 4 &= 0 \\[0.8em] x \cdot \Big( \underbrace{x^{2} - 4x - 1 + \textcolor{#cc071e}{\frac{4}{x}}}_{\textcolor{#cc071e}{\text{kein quadratischer Term}}} \Big) &= 0 \end{align*}\]
Weil der Faktor \(\left( x^{2} - 4x - 1 + \frac{4}{x} \right)\) kein quadratischer Term ist, können dessen Nullstellen nicht mithilfe der Lösungsformel für quadratische Gleichungen (Mitternachtsformel) berechnet werden.
Da Ausklammern von \(x\) nicht sinnvoll ist, wird eine Nullstelle durch Probieren bestimmt, mit dem Ziel einer anschließenden Polynomdivision.
\[f(x) = x^{3} - 4x^{2} - x + 4\]
Alle Koeffizienten \(a_{n} \dots a_{0}\) sind ganzzahlig. Deshalb kommen als ganzzahlige Nullstellen nur ganzzahlige Teiler von \(a_{0} = 4\) in Frage, also \(-1\), \(+1\), \(-2\), \(+2\), \(-4\) und \(+4\).
Beispielsweise ist \(x_{1} = 1\) eine ganzahlige Nullstelle von \(f\), denn
\(f(1) = 1^{3} - 4 \cdot 1^{2} - 1 + 4 = 1 - 4 - 1 + 4 = 0\).
Anmerkung:
Mit der „TABLE-Funktion" des Taschenrechners (Casio, MODE SETUP → 7) lassen sich Funktionswerte \(f(x)\) in ganzzahligen Schritten von \(x\) tabellarisch darstellen und ggf. diejenigen Werte für \(x\) finden, für die \(f(x) = 0\) gilt, also ganzzahlige Nullstellen, falls vorhanden.
Polynomdivision durchführen
Eine Polynomdivision ist die Division zweier Polynome. In diesem Fall ist der Dividend ein Polynom dritten Grades und der Divisor der zur Nullstelle \(x = 1\) gehörenden Linearfaktor \((x - 1)\), also ein Polynom ersten Grades (vgl. Produktform und Linearfaktoren einer ganzrationalen Funktion).
\[\underbrace{\underbrace{(\overbrace{x^{3} - 4x^{2} - x + 4}^{\text{Polynom 3. Grades}})}_{\text{Dividend}} : \underbrace{\overbrace{(x - 1)}^{\text{Linearfaktor}}}_{\text{Divisor}}}_{\text{Polynomdivision}} = \; ?\]
Das Ergebnis dieser Polynomdivision ist ein quadratischer Term, dessen Nullstellen sich mithilfe der Lösungsformel für quadratische Gleichungen (Mitternachtsformel) berechnen lassen (vgl. Abiturskript - 1.1.2 Quadratische Funktion).
1. Schritt:
Die höchste Potenz (mit Koeffizienten) \(\textcolor{#e9b509}{x^{3}}\) des Dividenden-Polynoms durch \(\textcolor{#e9b509}{x}\) des Linearfaktors dividieren und das Ergebnis \(\textcolor{#e9b509}{x^{2}}\) notieren.
\[(\textcolor{#e9b509}{x^{3}} - 4x^{2} - x + 4) : (\textcolor{#e9b509}{x} - 1) = \textcolor{#e9b509}{x^{2}}\]
2. Schritt:
Das Ergebnis \(\textcolor{#e9b509}{x^{2}}\) mit dem Linearfaktor \(\textcolor{#e9b509}{(x - 1)}\) multiplizieren und das Ergebnis der Multiplikation vom Dividenden-Polynom subtrahieren (auf Vorzeichen achten).
\[\begin{align*}&(x^{3} - 4x^{2} - x + 4) : \textcolor{#e9b509}{(x - 1)} = \textcolor{#e9b509}{x^{2}} \\[0.8em] - &\underline{\textcolor{#e9b509}{(x^{3} - x^{2})}} \\[0.8em] & \enspace \; -3x^{2} - x + 4\end{align*}\]
3. Schritt:
Ab hier wiederholen sich die ersten beiden Schritte. Die höchste Potenz \(\textcolor{#e9b509}{-3x^{2}}\) des verbleibenden Dividenden-Polynoms durch \(\textcolor{#e9b509}{x}\) des Linearfaktors dividieren und das Ergebnis \(\textcolor{#e9b509}{-3x}\) notieren.
\[\begin{align*}&(x^{3} - 4x^{2} - x + 4) : (\textcolor{#e9b509}{x} - 1) = x^{2} \textcolor{#e9b509}{-3x} \\[0.8em] - &\underline{(x^{3} - x^{2})} \\[0.8em] & \quad \; \textcolor{#e9b509}{-3x^{2}} - x + 4\end{align*}\]
4. Schritt:
Das Ergebnis \(\textcolor{#e9b509}{-3x}\) mit dem Linearfaktor \(\textcolor{#e9b509}{(x - 1)}\) multiplizieren und das Ergebnis der Multiplikation vom Dividenden-Polynom subtrahieren (auf Vorzeichen achten).
\[\begin{align*}&\quad \;(x^{3} - 4x^{2} - x + 4) : \textcolor{#e9b509}{(x - 1)} = x^{2} \textcolor{#e9b509}{-3x} \\[0.8em] &-\underline{(x^{3} - x^{2})} \\[0.8em] & \quad \quad-3x^{2} - x + 4 \\[0.8em] & \enspace \; -\underline{\textcolor{#e9b509}{(-3x^{2} + 3x)}} \\[0.8em] & \qquad \qquad \enspace -4x + 4 \end{align*}\]
5. Schritt:
Die höchste Potenz \(\textcolor{#e9b509}{-4x}\) des verbleibenden Dividenden-Polynoms durch \(\textcolor{#e9b509}{x}\) des Linearfaktors dividieren und das Ergebnis \(\textcolor{#e9b509}{-4}\) notieren.
\[\begin{align*}&\quad \;(x^{3} - 4x^{2} - x + 4) : (\textcolor{#e9b509}{x} - 1) = x^{2} -3x \textcolor{#e9b509}{-4} \\[0.8em] &-\underline{(x^{3} - x^{2})} \\[0.8em] & \quad \quad-3x^{2} - x + 4 \\[0.8em] & \enspace \; -\underline{(-3x^{2} + 3x)} \\[0.8em] & \qquad \qquad \enspace \; \textcolor{#e9b509}{-\,4x} + 4 \end{align*}\]
6. Schritt:
Das Ergebnis \(\textcolor{#e9b509}{-4}\) mit dem Linearfaktor \(\textcolor{#e9b509}{(x - 1)}\) multiplizieren und das Ergebnis der Multiplikation vom Dividenden-Polynom subtrahieren (auf Vorzeichen achten).
\[\begin{align*}&\quad \;(x^{3} - 4x^{2} - x + 4) : \textcolor{#e9b509}{(x - 1)} = x^{2} -3x \textcolor{#e9b509}{-4} \\[0.8em] &-\underline{(x^{3} - x^{2})} \\[0.8em] & \quad \quad-3x^{2} - x + 4 \\[0.8em] & \enspace \; -\underline{(-3x^{2} + 3x)} \\[0.8em] & \qquad \qquad \enspace -4x + 4 \\[0.8em] & \qquad \quad \; -\underline{\textcolor{#e9ba09}{(-4x + 4)}} \\[0.8em] & \qquad \qquad \qquad \quad \enspace \; \, 0\end{align*}\]
Damit ist die Polynomdivision beendet und es gilt folglich:
\[\begin{align*} f(x) &= 0 \\[0.8em] x^{3} - 4x^{2} - x + 4 &= 0 \\[0.8em] (x - 1) \cdot (x^{2} - 3x - 4) &= 0 \end{align*}\]
Nach dem Satz vom Nullprodukt: „Ein Produkt ist gleich Null, wenn einer der Faktoren gleich Null ist." ist zu überprüfen, ob die quadratische Gleichung \(x^{2} - 3x - 4 = 0\) weitere Nullstellen der Funktion \(f\) liefert.
Mithilfe der Lösungsformel für quadratische Gleichungen (Mitternachtsformel) (vgl. Abiturskript - 1.1.2 Quadratische Funktion) ergibt sich:
\[x_{2,3} = \frac{3 \pm \sqrt{(-3)^{2} - 4 \cdot 1 \cdot (-4)}}{2 \cdot 1} = \frac{3 \pm \sqrt{25}}{2} = \frac{3 \pm 5}{2}\]
\[x_{2} = \frac{3 - 5}{2} = \frac{-2}{2} = -1\]
\[x_{3} = \frac{3 + 5}{2} = \frac{8}{2} = 4\]
Die Funktion \(f \colon x \mapsto x^{3} - 4x^{2} -x + 4\) besitzt die Nullstellen \(x = -1\), \(x = 1\) und \(x = 4\).
3. Beispiel
Bestimmen Sie die Nullstellen der in \(\mathbb R\) definierten Funktion \(f \colon x \mapsto 2x^{4} - 4x^{2} - 6\).
\[\begin{align*} f(x) &= 0 \\[0.8em] 2x^{4} - 4x^{2} - 6 &= 0\end{align*}\]
In diesem Sonderfall ist eine sogenannte biquadratische Gleichung der Form \(ax^{4} + bx^{2} + c = 0\) zu lösen.
Das gelingt mithilfe folgender Substitution (Ersetzung):
1. Subsitution: \(x^{2} = u\)
2. Quadratische Gleichung mit der Variablen \(u\) lösen.
3. Rücksubstitution: \(u = x^{2}\)
4. Wurzel ziehen.
Substitution
\[\begin{align*} 2x^{4} - 4x^{2} - 6 &= 0 \\[0.8em] 2\left( x^{2} \right)^{2} - 4x^{2} - 6 &= 0 &&| \; \text{Substitution:}\; x^{2} = u \enspace (u > 0) \\[0.8em] 2u^{2} - 4u - 6 &= 0 \end{align*}\]
Quadratische Gleichung mit der Variablen \(u\) lösen
\[u_{1,2} = \frac{4 \pm \sqrt{(-4)^2 - 4 \cdot 2 \cdot (-6)}}{2 \cdot 2} = \frac{4 \pm \sqrt{64}}{4} = \frac{4 \pm 8}{4} = 1 \pm 2\]
\[u_{1} = 1 - 2 = -1\]
\[u_{2} = 1 + 2 = 3\]
Bei der Substitution \(x^{2} = u\) gilt \(u > 0\), weil \(x^{2}\) stets positiv ist. Die rechnerische Lösung \(u_{1} = -1\) ist eine Scheinlösung. deren Rücksubstitution \(-1 = x^{2}\) keine Lösung für \(x\) liefert. Solche Scheinlösungen können auftreten, da die Substitution \(x^{2} = u\) keine Äquivalenzumformung ist.
Rücksubstitution
\[\begin{align*}u_{2} &= x^{2} \\[0.8em] 3 &= x^{2}\end{align*}\]
Wurzel ziehen
\[\begin{align*} x^{2} &= 3 &&| \; \sqrt{\quad} \\[0.8em] x_{1,2} &= \pm \sqrt{3} \end{align*}\]
Die Funktion \(f \colon x \mapsto 2x^{4} - 4x^{2} - 6\) besitzt die Nullstellen \(x = -\sqrt{3}\) und \(x = \sqrt{3}\).
Symmetrieverhalten ganzrationaler Funktionen
Der Graph einer ganzrationalen Funktion \(f\colon x \mapsto a_{n}x^{n} + a_{n-1}x^{n-1} + \textstyle{\dots} + a_{1}x + a_{0}\) ist
achsensymmetrisch zur \(\boldsymbol{y}\)-Achse, wenn der Funktionsterm nur gerade Potenzen enthält. Das konstante Glied \(\boldsymbol{a_{0}}\) darf enthalten sein.
punktsymmetrisch zum Ursprung, wenn der Funktionsterm nur ungerade Potenzen enthält. Das konstante Glied \(\boldsymbol{a_{0}}\) darf nicht enthalten sein.
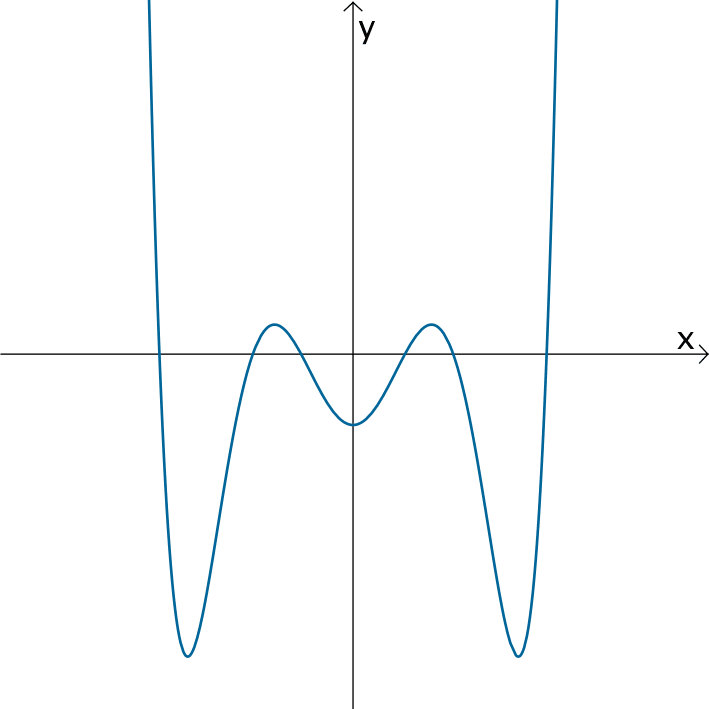
Der Graph der ganzrationalen Funktion \(f\colon x \mapsto 4x^{6} - 10 x^{4} + 5x^{2} -0{,}5\) ist achsensymmetrisch zur \(y\)-Achse.
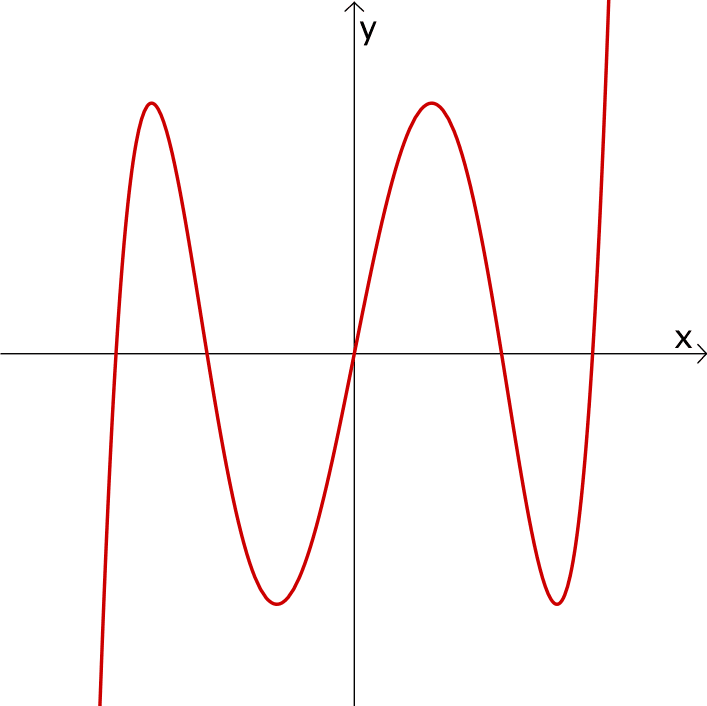
Der Graph der ganzrationalen Funktion \(f\colon x \mapsto 4x^{5} - 10x^{3} + 5x\) ist punktsymmetrisch zum Ursprung.
Verhalten für \(x \to -\infty\) und \(x \to +\infty\)
Bei einer ganzrationalen Funktion \(f\colon x \mapsto a_{n}x^{n} + a_{n-1}x^{n-1} + \textstyle{\dots} + a_{1}x + a_{0}\) bestimmt der Term \(a_{n}x^{n}\) das Verhalten des Graphen von \(f\) im Unendlichen.
\[\lim \limits_{x \,\to\,-\infty} a_{n}x^{n} + a_{n-1}x^{n-1} + \textstyle{\dots} + a_{1}x + a_{0} = \lim \limits_{x\,\to\,-\infty} a_{n}x^{n}\]
bzw.
\[\lim \limits_{x \,\to\,+\infty} a_{n}x^{n} + a_{n-1}x^{n-1} + \textstyle{\dots} + a_{1}x + a_{0} = \lim \limits_{x\,\to\,+\infty} a_{n}x^{n}\]
Beispielaufgabe
Bestimmen Sie Lage und Art aller Nullstellen der Funktion \(f\colon x \mapsto x^{3} - 6x^{2} + 9x\) und geben Sie den Funktionsterm \(f(x)\) in der vollständig faktorisierten Form an. Untersuchen Sie das Symmetrieverhalten des Graphen der Funktion \(f\) sowie das Verhalten für \(x \to -\infty\) und \(x \to +\infty\).
\[f(x) = x^{3} - 6x^{2} + 9x\,; \enspace D_{f} = \mathbb R\]
Nullstellen der Funktion \(f\):
\[\begin{align*} f(x) &= 0 \\[0.8em] x^{3} - 6x^{2} + 9x &= 0 & &| \;\text{Faktor}\;x\;\text{ausklammern} \\[0.8em] x \left( x^{2} - 6x + 9 \right) &= 0 \end{align*}\]
Satz vom Nullprodukt anwenden:
„Ein Produkt ist gleich Null, wenn einer der Faktoren gleich Null ist."
\[x = 0 \quad \vee \quad x^{2} - 6x + 9 = 0\]
\(\Longrightarrow \quad x_{1} = 0\) ist einfache Nullstelle (mit Vorzeichenwechsel).
\[\begin{align*} \underbrace{x^{2} - 6x + 9}_{a^{2}\,-\,2ab\,+\,b^{2}\,=\,(a\,-\,b)^{2}} &= 0 & &| \;\text{2. Binomische Formel anwenden} \\[0.8em] (x - 3)^{2} &= 0 \end{align*}\]
\(\Longrightarrow \quad x_{2} = 3\) ist doppelte Nullstelle (ohne Vorzeichenwechsel).
Funktionsterm \(f(x)\) in vollständig faktorisierter Form:
\[f(x) = x(x - 3)^{2}\]
Symmetrieverhalten des Graphen der Funktion \(f\):
Da der Funktionsterm \(f(x) = x^{3} - 6x^{2} + 9x\) sowohl gerade als auch ungerade Potenzen enthält, ist der Graph der Funktion \(f\) weder achsensymmetrisch zur \(y\)-Achse noch punktsymmetrisch zum Ursprung.
Als Alternative kann auch \(f(-x)\) untersucht werden (vgl. Abiturskript - 1.1.9 Symmetrieverhalten (bzgl. des Koordinatensystems)).
\[\begin{align*}f(-x) &= (-x)^{3} - 6 \cdot (-x)^{2} + 9 \cdot (-x) \\[0.8em] &= -x^{3} - 6x^{2} - 9x \\[0.8em] &= -\left( x^{3} + 6x^{2} + 9x \right)\end{align*}\]
\[\Longrightarrow \quad f(-x) \neq f(x)\,; \enspace f(-x) \neq -f(x)\]
\(\Longrightarrow \quad\)Der Graph der Funktion \(f\) ist weder achsensymmetrisch zur \(y\)-Achse noch punktsymmetrisch zum Ursprung.
Verhalten von \(f\) für \(x \to -\infty\) und \(x \to +\infty\):
\[f(x) = x^{3} - 6x^{2} + 9x\]
Die höchste Potenz, der Term \(x^{3}\), bestimmt das Verhalten des Graphen von \(f\) im Unendlichen.
\[\lim \limits_{x\, \to\,-\infty } x^{3} -6x^{2} + 9x = \lim \limits_{x\,\to\,-\infty} x^{3} = -\infty\]
\[\lim \limits_{x\, \to\,+\infty } x^{3} -6x^{2} + 9x = \lim \limits_{x\,\to\,+\infty} x^{3} = +\infty\]
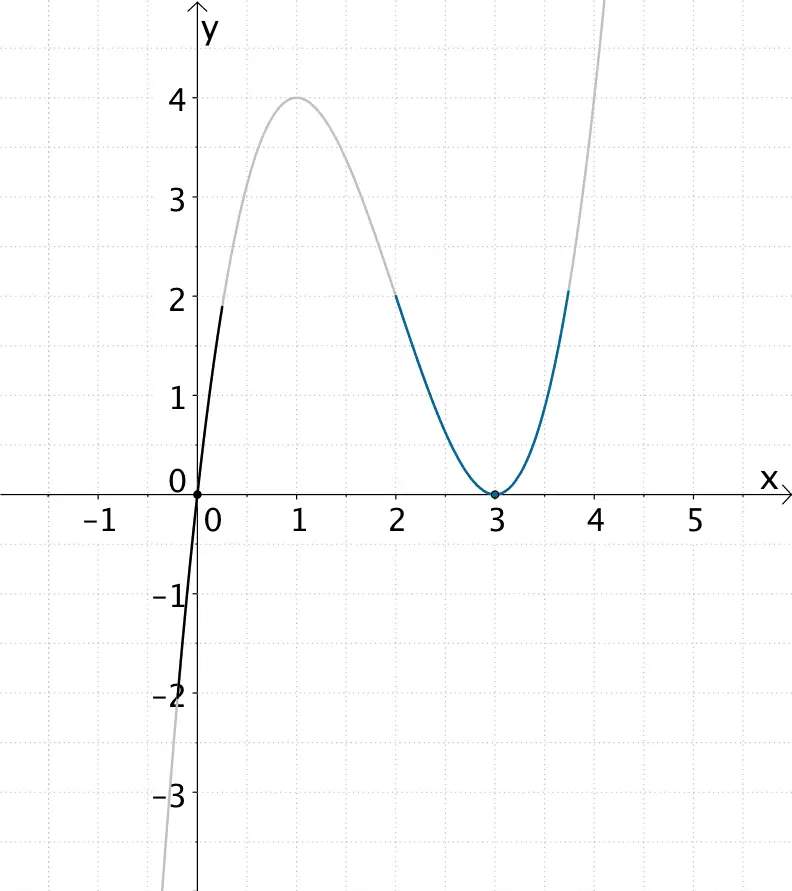
Graph der ganzrationalen Funktion \(f\colon x \mapsto x^{3} - 6x^{2} + 9x\) mit einfacher Nullstelle \(x_{1} = 0\) und doppelter Nullstelle \(x_{2} = 3\)

