Schnittstellen mit der \(x\)-Achse - Nullstellen
Für die Berechnung der Nullstelle(n) \(x_{i}\) einer Funktion \(f\) wird der Funktionsterm \(f(x)\) gleich null gesetzt.
\[f(x) = 0 \quad \Longrightarrow \quad N(x_{i}|0)\]
Schnittstelle mit der \(y\)-Achse
Für die Bestimmung der Schnittstelle des Graphen einer Funktion \(f\) mit der \(y\)-Achse wird der Funktionswert \(f(0)\) berechnet.
\(f(0)\) berechnen \(\quad \Longrightarrow \quad S_{y}(0|f(0))\)
Beispielaufgabe
Gegeben sei die Funktion \(f\colon x \mapsto 0{,}1(x^{2} - 4)(e^{x} + 1)(\ln x - 1)\left(\frac{1}{x} - 2 \right)\) mit maximaler Definitionsmenge \(D_{f}\). Geben Sie \(D_{f}\) an und bestimmen Sie alle Nullstellen der Funktion \(f\).
\[f(x) = 0{,}1(x^{2} - 4)(e^{x} + 1)(\ln x - 1)\left(\frac{1}{x} - 2 \right)\]
Maximale Definitionsmenge \(D_{f}\):
Die Logarithmusfunktion schränkt den Definitionsbereich ein. Die (natürliche) Logarithmusfunktion \(x \mapsto \ln x\) ist in \(\mathbb R^{+}\) definiert.
\[\Longrightarrow \quad D_{f} = \mathbb R^{+}\]
Nullstellen der Funktion \(f\):
Satz vom Nullprodukt: Ein Produkt ist genau dann gleich null, wenn einer der Faktoren gleich null ist.
\[f(x) = 0{,}1(x^{2} - 4)(\underbrace{e^{x} + 1}_{> \, 0})(\ln x - 1)\left(\frac{1}{x} - 2 \right)\]
\[\begin{align*} f(x) = 0 \quad \Longrightarrow \quad & & x^{2} - 4 &= 0 \\[0.8em] &\vee & \ln x - 1 &= 0 \\[0.8em] &\vee & \frac{1}{x} - 2 &= 0 \end{align*}\]
\[\begin{align*}x^{2} - 4 &= 0 & &| + 4 \\[0.8em] x^{2} &= 4 & &| \; \sqrt{\enspace} \enspace (D_{f} = \mathbb R^{+}) \\[0.8em] x &= 2\end{align*}\]
\[\begin{align*} \ln x - 1 &= 0 & &| + 1 \\[0.8em] \ln x &= 1 & &| \; \log_{a}a = 1 \\[0.8em] x &= e \end{align*}\]
\[\begin{align*} \frac{1}{x} - 2 &= 0 & &| + 2 \\[0.8em] \frac{1}{x} &= 2 & &| \cdot x \\[0.8em] 1 &= 2x & &| : 2 \\[0.8em] 0{,}5 &= x \end{align*}\]
Die Nullstellen der Funktion \(f\) sind: \(x_{1} = 0{,}5\), \(x_{2} = 2\) und \(x_{3} = e\).
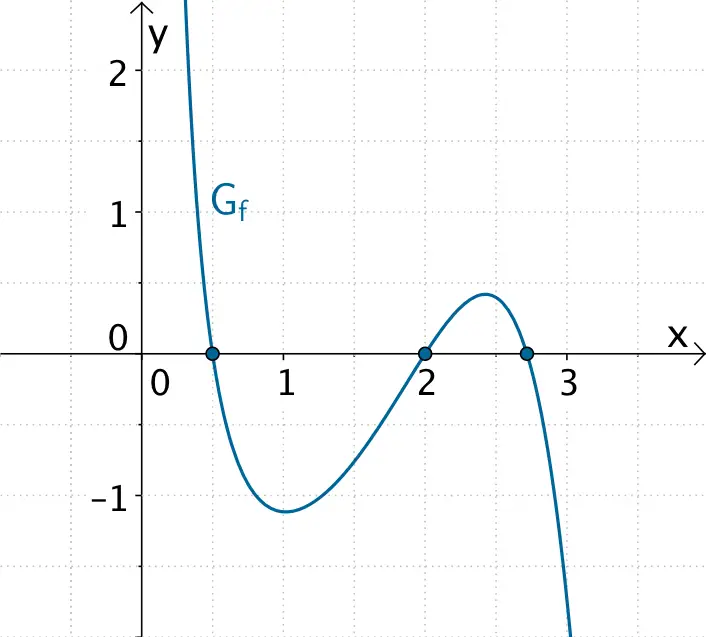
Graph der Funktion \(f\colon x \mapsto 0{,}1(x^{2} - 4)(e^{x} + 1)(\ln x - 1)\left(\frac{1}{x} - 2 \right)\) mit Nullstellen \(x_{1} = 0{,}5\), \(x_{2} = 2\) und \(x_{3} = e\)


