Natürliche Exponential- und Logarithmusfunktion
Die Exponentialfunktion \(f \colon x \mapsto e^{x}\) heißt Natürliche Exponentialfunktion Dabei ist \(e\) die durch den Grenzwert \(e = \lim \limits_{n \, \to \, \infty} \left( 1 + \frac{1}{n} \right)^{n} = 2{,}718281 \dots\) definierte Eulersche Zahl. Die Natürliche Exponentialfunktion wird auch als \(e\)-Funktion bezeichnet.
Die Logarithmusfunktion \(f \colon x \mapsto \ln x\) heißt Natürliche Logarithmusfunktion. Dabei bezeichnet \(\ln\) den Logarithmus zur Basis \(e\) (\(\ln x = \log_{e} x\)).
Eigenschaften der Natürlichen Exponential- und Logarithmusfunktion
| Natürliche Exponentialfunktion \(f \colon x \mapsto e^{x}\) | Natürliche Logarithmusfunktion \(f \colon x \mapsto \ln x\) | |
| Definitionsmenge | \(D_{f} = \mathbb R\) | \(D_{f} = \mathbb R^{+}\) |
| Wertemenge |
\(\begin{align*}&W_{f} = \mathbb R^{+} \\ &(e^{x} > 0 \; \text{für alle} \; x \in \mathbb R) \end{align*}\)
|
\(W_{f} = \mathbb R\) |
| Nullstelle | Keine Nullstelle | Einzige Nullstelle: \(x = 1\) |
| Asymptote | \(x\)-Achse: \(y = 0\) | \(y\)-Achse: \(x = 0\) |
| Wichtige Grenzwerte |
\(\begin{align*}\lim \limits_{x \, \to \, -\infty} e^{x} &= 0^{+} \\[0.8em] \lim \limits_{x \, \to \, +\infty} e^{x} &= +\infty \end{align*}\)
|
\(\begin{align*}\lim \limits_{x \, \to \, 0^{+}} \ln x &= -\infty \\[0.8em] \lim \limits_{x \, \to \, +\infty} \ln x &= +\infty \end{align*}\)
|
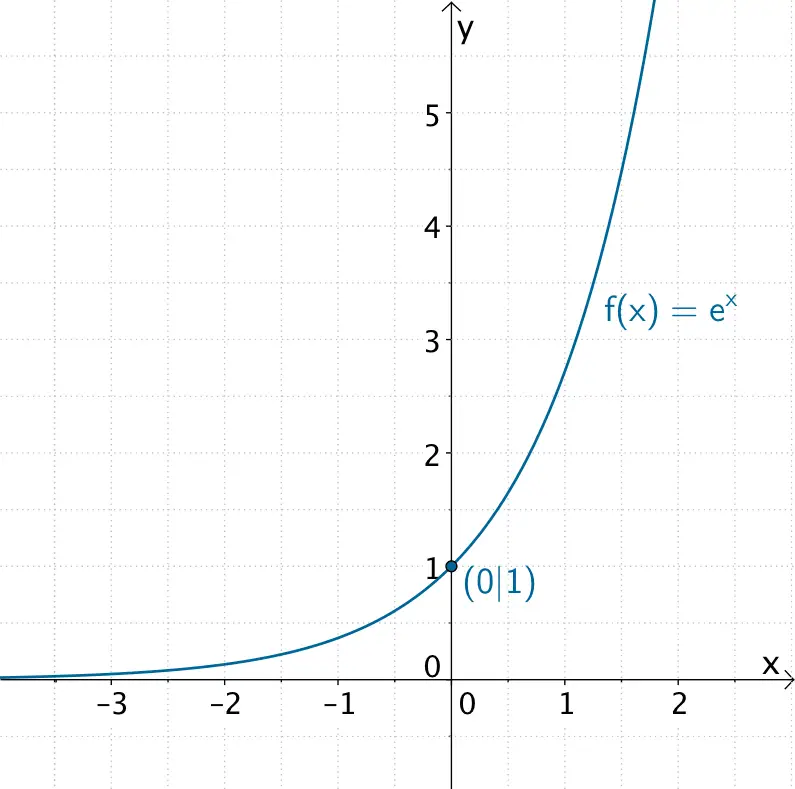
Graph der Natürlichen Exponentialfunktion \(f \colon x \mapsto e^{x}\)
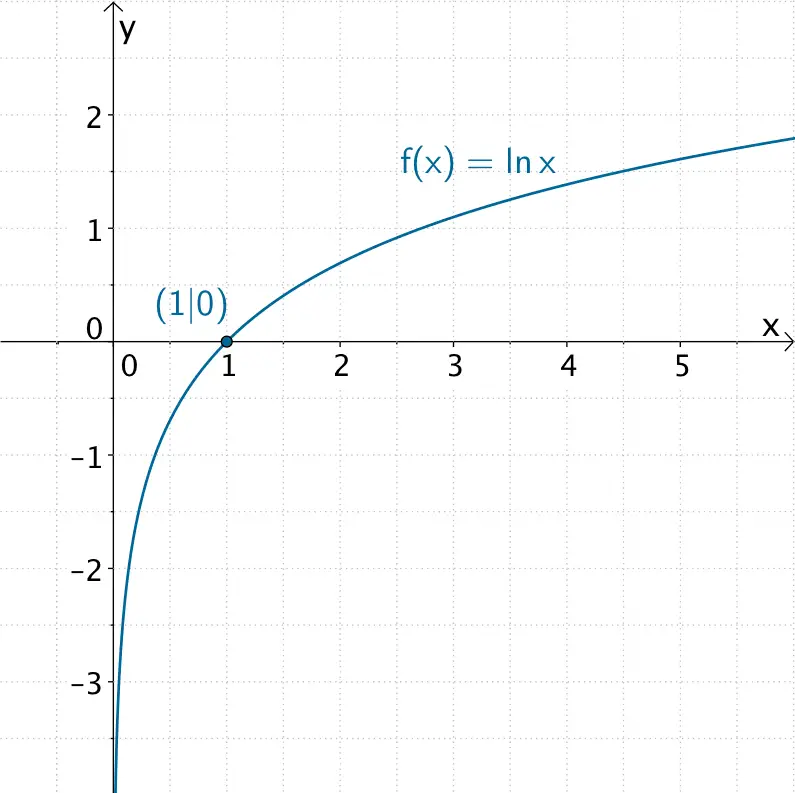
Graph der Natürlichen Logarithmusfunktion \(f \colon x \mapsto \ln x\)
Die Natürliche Exponential- und die natürliche Logarithmusfunktion sind voneinander Umkehrfunktionen (vgl. Abiturskript - 1.5.6 Umkehrfunktion).
Rechenregeln
Es gelten Folgende Rechenregeln:
\[\begin{align*}e^{0} &= 1 & & & \ln 1 &= 0 \\[0.8em] e^{1} &= e & & & \ln e &= 1 \\[0.8em] e^{\ln x} &= x & & & \ln{e^{x}} &= x \\[0.8em] \text{allg.:}\enspace a^{\log_{a}{x}} &= x & & & \log_{a}{a^{x}} &= x \quad (a > 0, \, a\neq 1) \end{align*}\]
Darüber hinaus finden die Rechenregeln für Potenzen und die Rechenregeln für Logarithmen Anwendung (vgl. Merkhilfe).
Rechenregeln für Potenzen
Für \(a, b \in \mathbb R \backslash \{0\}\) und \(m, n \in \mathbb Z\) bzw. \(a, b \in \mathbb R^{+}\) und \(m, n \in \mathbb R\) gilt:
| \(a^{m} \cdot a^{n} = a^{m + n}\) | \(\dfrac{a^{m}}{a^{n}} = a^{m - n}\) | \(\left(a^{m}\right)^{n} = a^{m \cdot n}\) |
| \(a^{m} \cdot b^{m} = (a \cdot b)^{m}\) | \(\dfrac{a^{m}}{b^{m}} = \left(\dfrac{a}{b}\right)^{m}\) |
Außerdem gilt:
\(a^{-n} = \dfrac{1}{a^{n}}\) für \(a \in \mathbb R \backslash \{0\}\) und \(n \in \mathbb N\)
\(a^{\frac{m}{n}} = \sqrt[n]{a^{m}}\) für \(a \in \mathbb R^{+}\) und \(m \in \mathbb Z, \, n \in \mathbb N\)
Rechenregeln für Logarithmen
Für \(a \in \mathbb R^{+}\) mit \(a \neq 1\) und \(b, c \in \mathbb R^{+}\) sowie \(n \in \mathbb R\) gilt:
| \(\log_{a}(b \cdot c) = \log_{a}b + \log_{a}c\) |
| \(\log_{a}\left( \dfrac{b}{c}\right) = \log_{a}b - \log_{a}c\) |
| \(\log_{a}{b^{n}} = n \cdot \log_{a}b\) |
Beispielaufgabe
Gegeben sei die Funktion \(f \colon x \mapsto \dfrac{1}{e^{x} \cdot e^{x + 1}} \cdot \ln{(x + 3)}\) mit maximaler Definitionsmenge \(D_{f}\).
Bestimmen Sie \(D_{f}\) sowie die Nullstelle der Funktion \(f\). Untersuchen Sie das Verhalten der Funktion \(f\) an den Rändern ihres Definitionsbereichs \(D_{f}\)?
Maximale Definitionsmenge \(D_{f}\):
Die (Natürliche) Logarithmusfunktion ist in \(\mathbb R^{+}\) definiert und schränkt damit die Definitionsmenge der Funktion \(f\) ein.
\[\begin{align*} \Longrightarrow \quad x + 3 &> 0 & &| - 3 \\[0.8em] x &> -3 \end{align*}\]
\[\Longrightarrow \quad D_{f} = \; ]-3;+\infty[\]
Nullstelle der Funktion \(f\):
Nullstelle(n) einer Funktion bestimmen
Eine Nullstelle ist die \(x\)-Koordinate eines gemeinsamen Punktes des Graphen einer Funktion \(x \mapsto f(x)\) mit der \(x\)-Achse. An einer Nullstelle gilt: \(f(x) = 0\).

Satz vom Nullprodukt: Ein Produkt ist genau dann null, wenn einer der Faktoren null ist.
\(f(x) \cdot g(x) = 0 \enspace \Rightarrow \enspace f(x) = 0\) oder \(g(x) = 0\)
Ein Quotient von Funktionen ist genau dann null, wenn die Zählerfunktion null ist.
\(\dfrac{f(x)}{g(x)} = 0 \enspace \Rightarrow \enspace f(x) = 0\; (g(x) \neq 0)\)
Lösungsformel für quadratische Gleichungen (Mitternachtsformel, vgl. Merkhilfe)
\[\textcolor{#cc071e}{a}x^2 + \textcolor{#0087c1}{b}x + \textcolor{#e9b509}{c} = 0 \enspace \Leftrightarrow \enspace x_{1,2} = \frac{-\textcolor{#0087c1}{b} \pm \sqrt{\textcolor{#0087c1}{b}^2 - 4\textcolor{#cc071e}{a}\textcolor{#e9b509}{c}}}{2\textcolor{#cc071e}{a}}\]
Diskriminante \(D = b^2 -4ac \;\):
\(D < 0\,\): keine Lösung
\(D = 0\,\): genau eine Lösung
\(D > 0\,\): zwei verschiedene Lösungen
Folgende Fälle lassen sich einfacher durch Umformung lösen:
\[\begin{align*}\textcolor{#cc071e}{a}x^2 + \textcolor{#0087c1}{b}x &= 0 &&| \; x\; \text{ausklammern (Produkt formulieren)} \\[0.8em] x \cdot (ax + b) &= 0 \\[0.8em] \Rightarrow \enspace x = 0 \vee ax + b &= 0 \end{align*}\]
\[\begin{align*}\textcolor{#cc071e}{a}x^2 + \textcolor{#e9b509}{c} &= 0 &&| -c \enspace (c \neq 0) \\[0.8em] ax^2 &= -c &&| : a \\[0.8em] x^2 &= -\frac{c}{a} &&| \; \sqrt{\quad} \\[0.8em] x_{1,2} &= \pm \sqrt{-\frac{c}{a}} \end{align*}\]
Zwei Lösungen, falls \(-\dfrac{c}{a} > 0\), keine Lösung, falls \(-\dfrac{c}{a} < 0\)
Vorgehensweise für die Bestimmung der Nullstelle(n) einer ganzrationalen Funktion ab Grad 3:
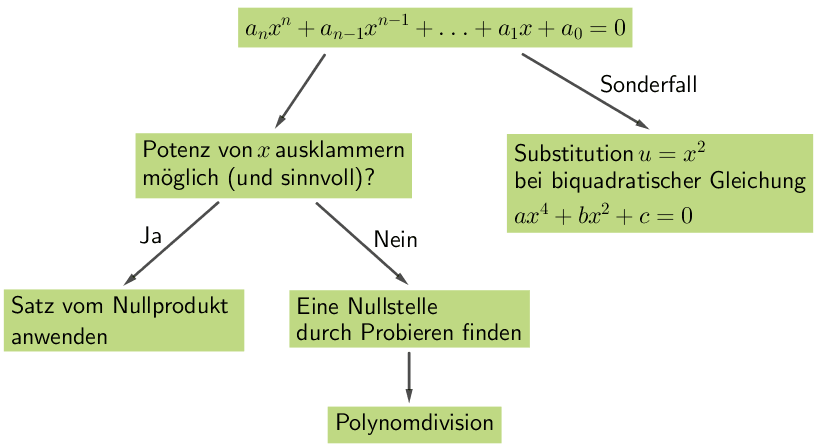
vgl. Abiturskript - 1.1.3 Ganzrationale Funktion, Nullstellen
Nullstellen einer gebrochenrationalen Funktion \(f(x) = \dfrac{\textcolor{#0087c1}{z(x)}}{n(x)}\) sind alle Nullstellen des Zählerpolynoms \(\textcolor{#0087c1}{z(x)}\), die nicht zugleich Nullstellen des Nennerpolynoms \(\boldsymbol{n(x)}\) sind.
Ist \(x_0\) eine Nullstelle des Zählerpolynoms \(\boldsymbol{z(x)}\) und zugleich eine vollständig kürzbare Nullstelle des Nennerpolynoms \(\boldsymbol{n(x)}\), so besitzt die gebrochenrationale Funktion \(f\) an der Stelle \(x_0\) eine hebbare Definitionslücke.
(vgl. Abiturskript - 1.2.1 Gebrochenrationale Funktion, Nullstellen und Polstellen)
Eine Wurzelfunktion \(f(x) = \sqrt{\textcolor{#cc071e}{g(x)}}\) nimmt genau dann den Wert null an, wenn der Radikand (Term unter der Wurzel) null ist.
\[\sin{x} = 0 \enspace \Rightarrow \enspace x = k \cdot \pi \; (k \in \mathbb Z)\]
\[\cos{x} = 0 \enspace \Rightarrow \enspace x = \dfrac{\pi}{2} + k \cdot \pi \; (k \in \mathbb Z)\]
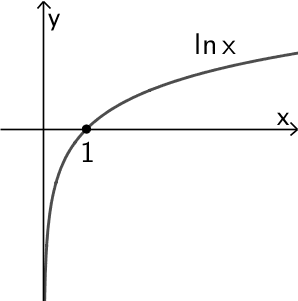
Die natürliche Logarithmusfunktion \(x \mapsto \ln{x}\) besitzt die einzige Nullstelle \(\boldsymbol{x = 1}\).
\[\ln{\left( \textcolor{#0087c1}{f(x)} \right)} = 0 \enspace \Rightarrow \enspace \textcolor{#0087c1}{f(x) = 1}\]
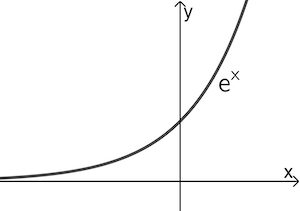
Die natürliche Exponentialfunktion \(x \mapsto e^x\) sowie jede verkettete Funktion \(x \mapsto e^{f(x)}\) besitzt keine Nullstelle!
\[\begin{align*} f(x) &= 0 \\[0.8em] \frac{1}{e^{x} \cdot e^{x + 1}} \cdot \ln{(x + 3)} &= 0 & &| \; a^{m} \cdot a^{n} = a^{m \cdot n} \\[0.8em] \frac{\ln{(x + 3)}}{e^{2x + 1}} &= 0 \end{align*}\]
\[\begin{align*}\Longrightarrow \quad \ln{(x + 3)} &= 0 & &| \; \ln 1 = 0 \\[0.8em] \Longrightarrow \quad x + 3 &= 1 & &| - 3 \\[0.8em] x &= -2 \end{align*}\]
Verhalten der Funktion \(f\) an den Rändern des Definitionsbereichs \(D_{f}\):
\[D_{f} = \; ]-3;+\infty[\]
\[\begin{align*}\lim \limits_{x \, \to \, -3^{+}} f(x) &= \lim \limits_{x \, \to \, -3^{+}} \frac{1}{e^{x} \cdot e^{x + 1}} \cdot \ln{(x + 3)} & &| \; \frac{1}{a^{n}} = a^{-n} \\[0.8em] &= \lim \limits_{x \, \to \, -3^{+}} \underbrace{e^{-(2x + 1)}}_{\to \, e^{5}} \cdot \underbrace{\ln{(x + 3)}}_{\to \, -\infty} \\[0.8em] &= -\infty \end{align*}\]
\[\lim \limits_{x \, \to \, +\infty} f(x) = \lim \limits_{x \, \to \, + \infty} \underbrace{\frac{1}{e^{2x + 1}}}_{\to \, 0} \cdot \underbrace{\ln{(x + 3)}}_{\to \, +\infty} = 0\]
Jede \(e\)-Funktion geht für \(x \to +\infty\) schneller gegen \(+\infty\) als jede (Natürliche) Logarithmusfunktion. Daher strebt der Term \(\dfrac{1}{e^{2x + 1}}\) schneller gegen Null als der Term \(\ln{(x + 3)}\) gegen \(+\infty\).
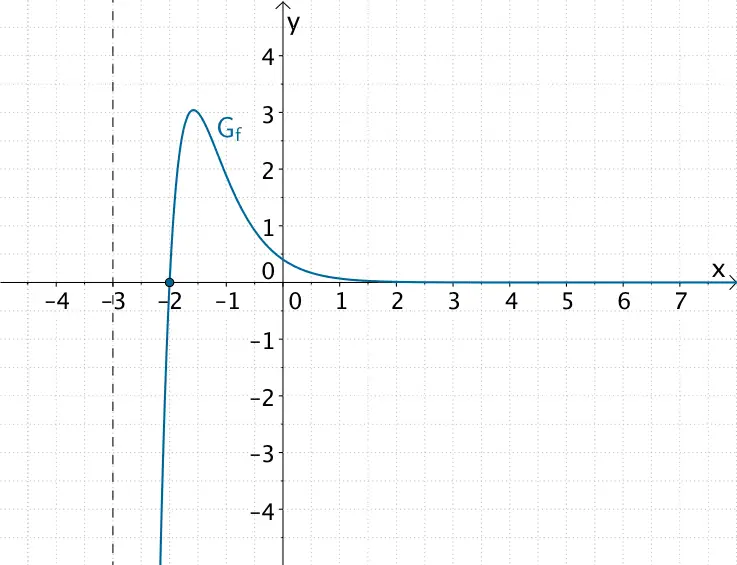
Graph der Funktion \(f \colon x \mapsto \dfrac{1}{e^{x} \cdot e^{x + 1}} \cdot \ln{(x + 3)}\)

