Exponentialgleichungen
Eine Gleichung, in der die unbekannte Größe nur im Exponenten von Potenzausdrücken vorkommt, wird als Exponentialgleichung bezeichnet. Für Exponentialgleichungen lässt sich kein allgemeines Lösungsverfahren angeben. Vielfach ist es möglich, Gleichungen dieser Art mithilfe elementarer Umformungen (vgl. Abiturskript - 1.3.1 Natürliche Exponential- und Logarithmusfunktion, Eigenschaften und Rechenregeln) und einer sich anschließenden Logarithmierung oder durch das Anwenden einer Substitution zu lösen.
1. Beispiel:
\[2e^{x - 2} - 4 = \frac{1}{e^{2 - x}}\]
Ein Logarithmieren der Gleichung ist zunächst nicht zielführend, da der Subtrahend \(4\) der Differenz \(2e^{x - 2} - 4\) das Auflösen des Exponetialterms \(2e^{x - 2}\) verhindert. Deshalb wird die Exponentialgleichung in einem ersten Schritt durch geeignete Umformung vereinfacht. In diesem Fall können die Exponentialterme zusammengefasst werden, sodass sich die Exponentialgleichung anschließend durch Logarithmieren lösen lässt.
\[\begin{align*}2e^{x - 2} - 4 &= \frac{1}{e^{2 - x}} & & | - \frac{1}{e^{2 - x}} + 4 \\[0.8em] 2e^{x - 2} - \frac{1}{e^{2 - x}} &= 4 & &| \: \frac{1}{a^{n}} = a^{-n} \\[0.8em] 2e^{x - 2} - e^{-(2 - x)} &= 4 \\[0.8em] 2e^{x - 2} - e^{x - 2} &= 4 \\[0.8em] e^{x - 2} &= 4 & &| \; \ln(\dots) \enspace \text{Logarithmieren} \\[0.8em] \ln \left( e^{x - 2} \right) &= \ln{4} & &| \; \ln {e^{x}} = x \enspace \left( \text{allg.:} \; \log_{a}{a^{x}} = x \right) \\[0.8em] x - 2 &= \ln{4} & &| + 2 \\[0.8em] x &= \ln{4} + 2 \\[0.8em] x &= \ln{2^{2}} + 2 & &| \; \log_{a}\left(b^{n}\right) = n \cdot \log_{a}{b} \\[0.8em] x &= 2\ln{2} + 2 \\[0.8em] x &\approx 3{,}39 \end{align*}\]
Die Exponentialgleichung besitzt genau eine Lösung \(x = 2\ln{2} + 2\).
2. Beispiel:
\[e^{4x + 2} = \frac{9}{4} + 4e^{2x + 1}\]
Ein Logarithmieren der Gleichung ist nicht sinnvoll, da der (Natürliche) Logarithmus der Summe \(\frac{9}{4} + 4e^{2x + 1}\) den Exponentialterm \(4e^{2x + 1}\) nicht auflöst.
Der Exponetialterm \(e^{4x + 2}\) ist gleich dem Quadrat des Exponentialterms \(e^{2x + 1}\), denn nach der Rechenregel für Potenzen \(a^{m \cdot n} = \left( a^{m} \right)^{n}\) gilt:
\[e^{4x + 2} = e^{2 \cdot (2x + 1)} = \left( e^{2x + 1} \right)^{2}\]
Somit lässt sich die vorliegende Exponentialgleichung durch die Substitution \(z = e^{2x + 1}\) in eine quadratische Gleichung überführen. Mithilfe der Lösungsformel für quadratische Gleichungen ergeben sich maximal zwei reelle Lösungen \(z_{1}\) und \(z_{2}\) (vgl. Abiturskript - 1.1.2 Quadratische Funktion, Lösungsformel für quadratische Gleichungen, vgl. Merkhilfe).
Die Rücksubstitution \(z_{1} = e^{2x + 1}\) bzw. \(z_{2} = e^{2x + 1}\) liefert die Lösung(en) der Exponetialgleichung.
\[\begin{align*}e^{4x + 2} &= \frac{9}{4} + 4e^{2x + 1} \\[0.8em] e^{2 \cdot (2x + 1)} &= \frac{9}{4} + 4e^{2x + 1} \\[0.8em] \left( e^{2x + 1} \right)^{2} &= \frac{9}{4} + 4e^{2x + 1} & &| - \frac{9}{4} - 4e^{2x + 1} \\[0.8em] \left( e^{2x + 1} \right)^{2} - 4e^{2x + 1} - \frac{9}{4} &= 0 \end{align*}\]
Substitution:
\(z = e^{2x + 1}\)
Mit \(z \in \mathbb R^{+}\), da \(e^{2x + 1} > 0\) für alle \(x \in \mathbb R\) gilt (vgl. Abiturskript - 1.3.1 Natürliche Exponential- und Logarithmusfunktion, Eigenschaften und Rechenregeln).
\[\Longrightarrow \quad z^{2} - 4z - \frac{9}{4} = 0\]
Lösungsformel für quadratische Gleichungen anwenden:
\[\begin{align*} z_{1,2} &= \frac{4 \pm \sqrt{(-4)^{2} - 4 \cdot 1 \cdot \left( -\frac{9}{4} \right)}}{2 \cdot 1} \\[0.8em] &= \frac{4 \pm \sqrt{16 + 9}}{2} \\[0.8em] &= \frac{4 \pm \sqrt{25}}{2} \\[0.8em] &= \frac{4 \pm 5}{2} \\[0.8em] &= 2 \pm 2{,}5\end{align*}\]
\[(z_{1} = 2 - 2{,}5 = -0{,}5)\]
\[z_{2} = 2 + 2{,}5 = 4{,}5\]
Rücksubstitution:
Für die Rücksubstitution ist mit \(z \in \mathbb R^{+}\) nur die Lösung \(z_{2} = 4{,}5\) von Belang.
\[\begin{align*} e^{2x + 1} &= z_{2} \\[0.8em] e^{2x + 1} &= 4{,}5 & &| \; \ln(\dots) \enspace \text{Logarithmieren} \\[0.8em] \ln\left( e^{2x + 1} \right) &= \ln{4{,}5} & &| \; \ln{e^{x}} = x \enspace \left( \text{allg.:} \; \log_{a}{a^{x}} = x \right) \\[0.8em] 2x + 1 &= \ln{4{,}5} & &| - 1 \\[0.8em] 2x &= \ln{4{,}5} - 1 & &| : 2 \\[0.8em] x &= \frac{\ln{4{,}5} - 1}{2} \\[0.8em] x &\approx 0{,}25 \end{align*}\]
Die Exponentialgleichung besitzt genau eine Lösung \(x = \dfrac{\ln{4{,}5} - 1}{2}\).
Logarithmusgleichungen
Eine Logarithmusgleichung liegt vor, wenn die unbekannte Größe nur im Argument von Logarithmusfunktionen auftritt. Logarithmusgleichungen lassen sich häufig durch elementare Umformungen (vgl. Abiturskript - 1.3.1 Natürliche Exponential- und Logarithmusfunktion, Eigenschaften und Rechenregeln) und einer sich anschließenden Entlogarithmierung lösen. Bei der Entlogarithmierung wird die Logarithmusgleichung zur Basis des auftretenden Logarithmus potenziert.
1. Beispiel:
\[\ln(2x - 1) + \ln{2} = 2\]
Die (Natürliche) Logarithmusfunktion ist in \(\mathbb R^{+}\) definiert (vgl. Abiturskript - 1.3.1 Natürliche Exponential- und Logarithmusfunktion, Eigenschaften und Rechenregeln). Die Lösungen der vorliegenden Logarithmusgleichung müssen die Bedingung \(2x - 1 > 0\) erfüllen.
\[\begin{align*} 2x - 1 > 0 & &| + 1 \\[0.8em] 2x > 1 & &| : 2 \\[0.8em] x > 0{,}5 \end{align*}\]
Es sind nur Lösungen aus dem Intervall \(x > 0{,}5\) möglich.
\[\begin{align*} \ln(2x - 1) + \ln{2} &= 2 & &| \; \log_{a}{b} + \log_{a}{c} = \log_{a}(b \cdot c) \\[0.8em] \ln[2 \cdot (2x - 1)] &= 2 \\[0.8em] \ln(4x - 2) &= 2 & &| \; e^{(\dots)} \enspace \text{Zur Basis}\; e \; \text{potenzieren} \\[0.8em] e^{\ln(4x - 2)} &= e^{2} & &| \; e^{\ln{x}} = x \enspace \left( \text{allg.:} \; a^{\log_{a}{x}} = x \right) \\[0.8em] 4x - 2 &= e^{2} & &| + 2 \\[0.8em] 4x &= e^{2} + 2 & &| : 4 \\[0.8em] x &= \frac{e^{2}}{4} + \frac{1}{2} \\[0.8em] x &\approx 2{,}35 \end{align*}\]
Die Logarithmusgleichung besitzt genau eine Lösung \(x = \dfrac{e^{2}}{4} + \dfrac{1}{2}\).
2. Beispiel:
\[\ln(x^{2} - 4) = \ln{x} + 1\]
Die (Natürliche) Logarithmusfunktion ist in \(\mathbb R^{+}\) definiert (vgl. Abiturskript - 1.3.1 Natürliche Exponential- und Logarithmusfunktion, Eigenschaften und Rechenregeln). Die Lösungen der vorliegenden Logarithmusgleichung müssen die Bedingungen \(x^{2} - 4 > 0\) und \(x > 0\) erfüllen.
\[\begin{align*} x^{2} - 4 &> 0 & &| + 4 \\[0.8em] x^{2} &> 4 & &| \; \sqrt{(\dots)} \enspace \text{Es gilt:} \; \sqrt{a^{2}} = \vert a \vert \; \text{mit} \; a \in \mathbb R \\[0.8em] \vert x \vert &> 2 \end{align*}\]
\[\vert x \vert = \begin{cases} \hspace{13px}x &\text{für} \quad x \geq 0 \\[0.8em] -x &\text{für} \quad x < 0 \end{cases}\]
(vgl. Abiturskript - 1.1.5 Betragsfunktion)
Fallunterscheidung:
1. Fall: \(x > 2\) für \(x \geq 0\)
2. Fall: \(-x > 2 \Leftrightarrow x < -2\) für \(x < 0\)
\[\Longrightarrow \quad x > 2 \vee x < -2\]
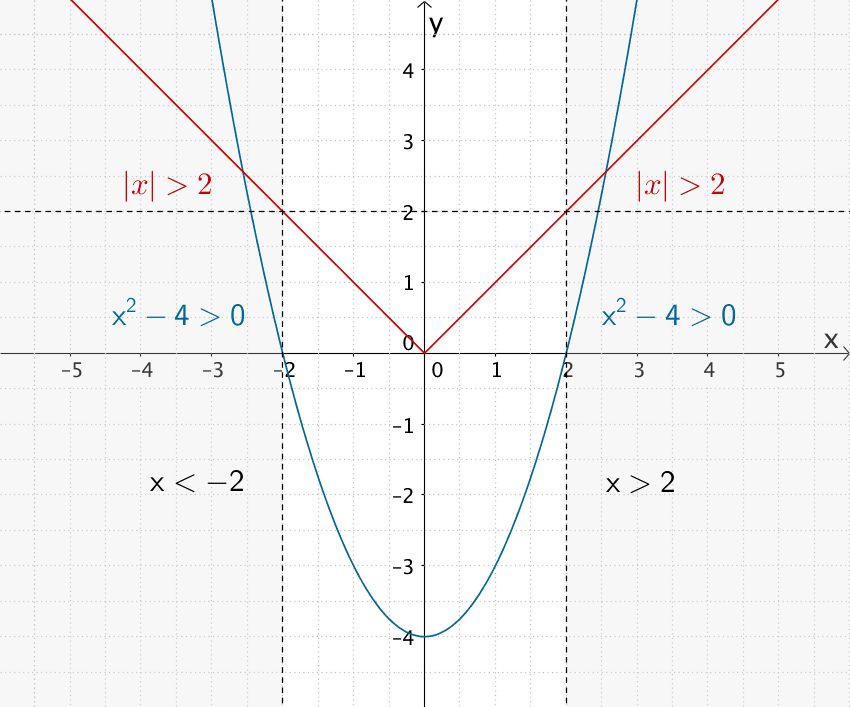
Veranschaulichung der Lösungen \(x > 2 \vee x < -2\) der Ungleichung \(x^{2} - 4 > 0\)
Die Lösungen der Logarithmusgleichung \(\ln(x^{2} - 4) = \ln{x} + 1\) müssen also die Bedingung \(x > 2 \vee x < -2\) und die Bedingung \(x > 0\) erfüllen.
Somit sind nur Lösungen aus dem Intervall \(x > 2\) möglich.
\[\begin{align*}\ln(x^{2} - 4) &= \ln{x} + 1 & &| \; \ln{e} = 1 \\[0.8em] \ln(x^{2} - 4) &= \ln{x} + \ln{e} & &| \log_{a}{b} + \log_{a}{c} = \log_{a}(b \cdot c) \\[0.8em] \ln(x^{2} - 4) &= \ln(ex) & &| \; e^{(\dots)} \enspace \text{Zur Basis}\; e \; \text{potenzieren} \\[0.8em] e^{\ln(x^{2} - 4)} &= e^{\ln(ex)} & &| \; e^{\ln{x}} = x \enspace \left( \text{allg.:}\; a^{\log_{a}{x}} = x \right) \\[0.8em] x^{2} - 4 &= ex & & | - ex \\[0.8em] x^{2} - ex - 4 &= 0 \end{align*}\]
Lösungsformel für quadratische Gleichungen anwenden (vgl. Abiturskript - 1.1.2 Quadratische Funktion, Lösungsformel für quadratische Gleichungen, vgl. Merkhilfe):
\[\begin{align*} x_{1,2} &= \frac{e \pm \sqrt{(-e)^{2} - 4 \cdot 1 \cdot (-4)}}{2 \cdot 1} \\[0.8em] &= \frac{e \pm \sqrt{e^{2} + 16}}{2} \end{align*}\]
\[\left( x_{1} = \frac{e - \sqrt{e^{2} + 16}}{2} \approx -1{,}06 \right)\]
\[x_{2} = \frac{e + \sqrt{e^{2} + 16}}{2} \approx 3{,}78\]
\(x = \dfrac{e + \sqrt{e^{2} + 16}}{2}\) ist einzige Lösung der Logarithmusgleichung.
Beispielaufgabe
Der Graph \(G_{f}\) der in \(\mathbb R\) definierten Funktion \(f \colon x \mapsto e^{x - 2} + 2\) und der Graph \(G_{g}\) der ebenfalls in \(\mathbb R\) definierten Funktion \(g \colon x \mapsto -\dfrac{1}{e^{4 - x}} + 4\) haben den einzigen gemeinsamen Punkt \(S\).
Ermitteln Sie einen Näherungswert für die \(x\)-Koordinate des Punktes \(S\), indem Sie \(G_{f}\) und \(G_{g}\) in ein gemeinsames Koordinatensystem skizzieren und den Punkt \(S\) kennzeichnen.
Bestimmen Sie die Lage des Punktes \(S\) durch Rechnung.
Skizzieren der Graphen \(G_{f}\) und \(G_{g}\)
Zunächst wird die Entstehung der Graphen der Funktionen \(f\) und \(g\) aus dem Graphen der Natürlichen Exponentialfunktion \(x \mapsto e^{x}\) untersucht. Anschließend lassen sich \(G_{f}\) und \(G_{g}\) anhand charakteristischer Punkte und Eigenschaften der Natürlichen Exponentialfunktion skizzieren.
\[f(x) = e^{x - 2} + 2; \; D = \mathbb R\]
Der Graph der Funktion \(f\) ist gegenüber dem Graphen der Natürlichen Exponentialfunktion \(x \mapsto e^{x}\) um \(+2\) in \(x\)-Richtung und um \(+2\) in \(y\)-Richtung verschoben (vgl. Abiturskript - 1.1.7 Entwicklung von Funktionen).
\[g(x) = -\frac{1}{e^{4 - x}} + 4; \; D = \mathbb R\]
\[\begin{align*}g(x) &= -\frac{1}{e^{4 - x}} + 4 & &| \; \frac{1}{a^{n}} = a^{-n} \\[0.8em] &= - e^{-(4 - x)} + 4 \\[0.8em] &= - e^{x - 4} + 4 \end{align*}\]
Der Graph der Funktion \(g\) geht aus dem Graphen der Natürlichen Exponentialfunktion \(x \mapsto e^{x}\) durch Spiegelung an der \(x\)-Achse sowie durch Verschiebung um \(+4\) in \(x\)-Richtung und um \(+4\) in \(y\)-Richtung hervor (vgl. Abiturskript - 1.1.7 Entwicklung von Funktionen).
Charakteristische Punkte und Eigenschaften des Graphen der Natürlichen Exponentialfunktion \(x \mapsto e^{x}\) (vgl. Abiturskript - 1.3.1 Natürliche Exponential- und Logarithmusfunktion, Eigenschaften und Rechenregeln):
Der Graph der Natürlichen Exponentialfunktion \(x \mapsto e^{x}\) verläuft stets oberhalb der \(x\)-Achse und durch die Punkte \((0|1)\) und \((1|e)\).
Für \(x \to -\infty\) nähert er sich asymptotisch der \(x\)-Achse an. Für \(x \to +\infty\) verläuft er steil gegen \(+\infty\).
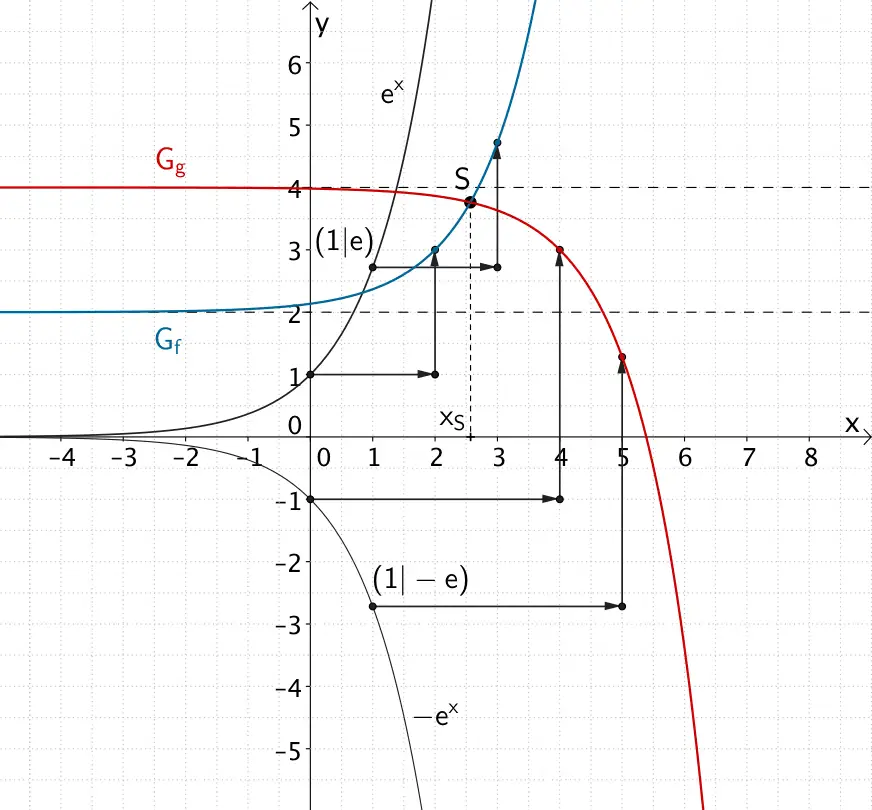
Entstehung des Graphen der Funktion \(f\) und des Graphen der Funktion \(g\) aus dem Graphen der Natürlichen Exponentialfunktion \(x \mapsto e^{x}\), Schnittpunkt \(S\) der Graphen \(G_{f}\) und \(G_{g}\)
Der Skizze entnimmt man die \(x\)-Koordinate des Schnittpunkts \(S\) zu \(x_{S} \approx 2{,}5\).
Bestimmung der Lage des Punktes \(S\) durch Rechnung
Für die Berechnung der \(x\)-Koordinate des Punktes \(S\) werden die Funktionsterme der Funktionen \(f\) und \(g\) gleichgesetzt. Es ergibt sich eine Exponentialgleichung, deren Lösung \(x_{S}\) ist.
\[f(x) = e^{x - 2} + 2\]
\[g(x) = -\frac{1}{e^{4 - x}} + 4\]
\[\begin{align*} e^{x - 2} + 2 &= -\frac{1}{e^{4 - x}} + 4 & &| \; \frac{1}{a^{n}} = a^{-n} \\[0.8em] e^{x - 2} + 2 &= - e^{-(4 - x)} + 4 \\[0.8em] e^{x - 2} + 2 &= - e^{x - 4} + 4 & &| + e^{x - 4} - 2 \\[0.8em] e^{x - 2} + e^{x - 4} &= 2 & &| \; a^{m - n} = \frac{a^{m}}{a^{n}} \\[0.8em] \frac{e^{x}}{e^{2}} + \frac{e^{x}}{e^{4}} &= 2 \\[0.8em] \frac{e^{2} \cdot e^{x}}{e^{4}} + \frac{e^{x}}{e^{4}} &= 2 \\[0.8em] \frac{e^{x}\left( e^{2} + 1 \right)}{e^{4}} &= 2 & &| \cdot e^{4} \\[0.8em] e^{x} \left( e^{2} + 1 \right) &= 2e^{4} & &| : \left(e^{2} + 1 \right) \\[0.8em] e^{x} &= \frac{2e^{4}}{e^{2} + 1} & &| \: \ln(\dots) \enspace \text{Logarithmieren} \\[0.8em] \ln\left( e^{x} \right) &= \ln\left( \frac{2e^{4}}{e^{2} + 1} \right) & &| \; \ln{e^{x}} = x \enspace \left( \text{allg.:} \; \log_{a}{a^{x}} = x \right) \\[0.8em] x &= \ln\left( \frac{2e^{4}}{e^{2} + 1} \right) \\[0.8em] x &\approx 2{,}57 \end{align*}\]
\[\Longrightarrow \quad x_{S} = \ln\left( \frac{2e^{4}}{e^{2} + 1} \right) \approx 2{,}57\]
\(y\)-Koordinate des Punktes \(S\) berechnen:
\[f(x) = e^{x - 2} + 2\]
\[\begin{align*} y_{S} = f(x_{S}) &= e^{\left[\ln\left( \frac{2e^{4}}{e^{2} + 1} \right) - 2 \right]} + 2 & &| \; a^{m - n} = \frac{a^{m}}{a^{n}} \\[0.8em] &= \frac{e^{\ln\left( \frac{2e^{4}}{e^{2} + 1} \right)}}{e^{2}} + 2 & &| \; e^{\ln{x}} = x \enspace \left( \text{allg.:} \; a^{\log_{a}{x}} = x \right) \\[0.8em] &= \frac{\frac{2e^{2} \cdot \cancel{e^{2}}}{e^{2} + 1}}{\cancel{e^{2}}} + 2 \\[0.8em] &= \frac{2e^{2}}{e^{2} + 1} + 2 \\[0.8em] &\approx 3{,}76 \end{align*}\]
\(\Longrightarrow \quad S \left(\ln\left( \dfrac{2e^{4}}{e^{2} + 1} \right) \bigg| \dfrac{2e^{2}}{e^{2} + 1} + 2 \right)\) bzw. \(S(2{,}57|3{,}76)\)
oder
\(g(x) = -\dfrac{1}{e^{4 - x}} + 4 = -e^{x - 4} + 4\) (vgl. oben)
\[\begin{align*} y_{S} = g(x_{S}) &= -e^{\left[ \ln\left( \frac{2e^{4}}{e^{2} + 1} \right) - 4 \right]} + 4 & &| \; a^{m - n} = \frac{a^{m}}{a^{n}} \\[0.8em] &= -\frac{e^{\ln\left( \frac{2e^{4}}{e^{2} + 1} \right)}}{e^{4}} + 4 & &| e^{\ln{x}} = x \enspace \left( \text{allg.:}\; a^{\log_{a}{x}} = x \right) \\[0.8em] &= - \frac{\frac{2 \cancel{e^{4}}}{e^{2} + 1}}{\cancel{e^{4}}} + 4 \\[0.8em] &= 4 - \frac{2}{e^{2} + 1} \\[0.8em] &\approx 3{,}76 \end{align*}\]
\(\Longrightarrow \quad S \left(\ln\left( \dfrac{2e^{4}}{e^{2} + 1} \right) \bigg| 4 - \dfrac{2}{e^{2} + 1}\right)\) bzw. \(S(2{,}57|3{,}76)\)


