Differenzenquotient (mittlere Änderungsrate) und Differentialquotient (lokale bzw. momentane Änderungsrate)
Differenzenquotient oder mittlere Änderungsrate
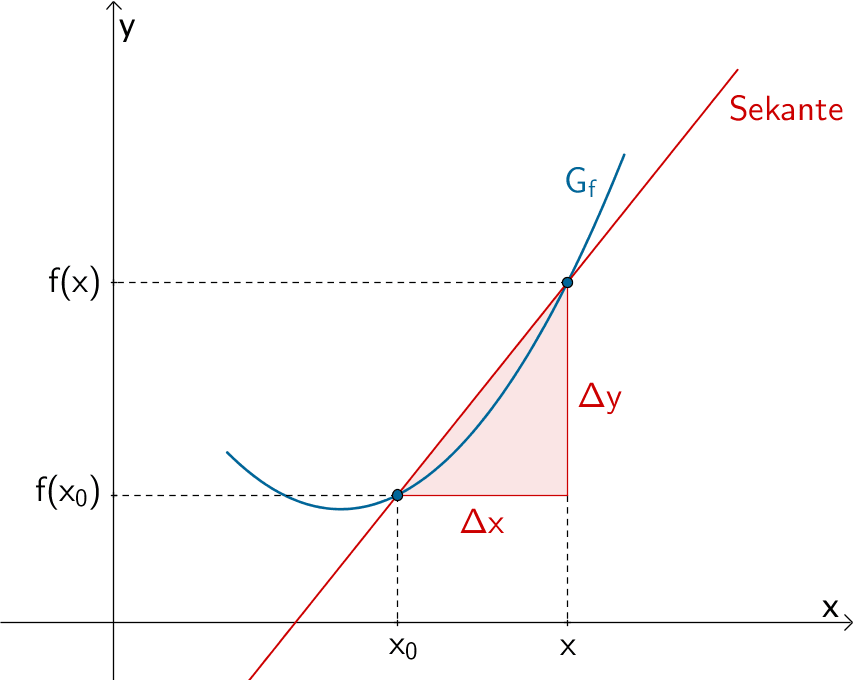
Der Differenzenquotient oder die mittlere Änderungsrate \(m_{s} = \dfrac{f(x) - f(x_{0})}{x - x_{0}}\) beschreibt die Steigung der Sekante durch den Punkt \((x_{0}|f(x_{0}))\) und einen weiteren Punkt des Graphen der Funktion \(f\).
Differenzenquotient oder mittlere Änderungsrate
\[m_{s} = \frac{f(x) - f(x_{0})}{x - x_{0}}\]
(vgl. Merkhilfe)
Bedeutung im zeitlichen Sachzusammenhang:
Beschreibt eine Funktion den Wert einer Größe in Abhängigkeit von der Zeit, so bedeutet der Differenzenquotient die mittlere (durchschnittliche) Änderung der Größe pro Zeiteinheit für einen betrachteten Zeitraum.
Beschreibt beispielsweise eine Funktion die Schadstoffemission eines Schornsteins in Kubikmetern in Abhängigkeit von der Zeit in Minuten, so bedeutet der Differenzenquotient in diesem Sachzusammenhang die mittlere Emissionsrate in Kubikmeter pro Minute für einen betrachteten Zeitraum.
Differentialquotient oder lokale bzw. momentane Änderungsrate
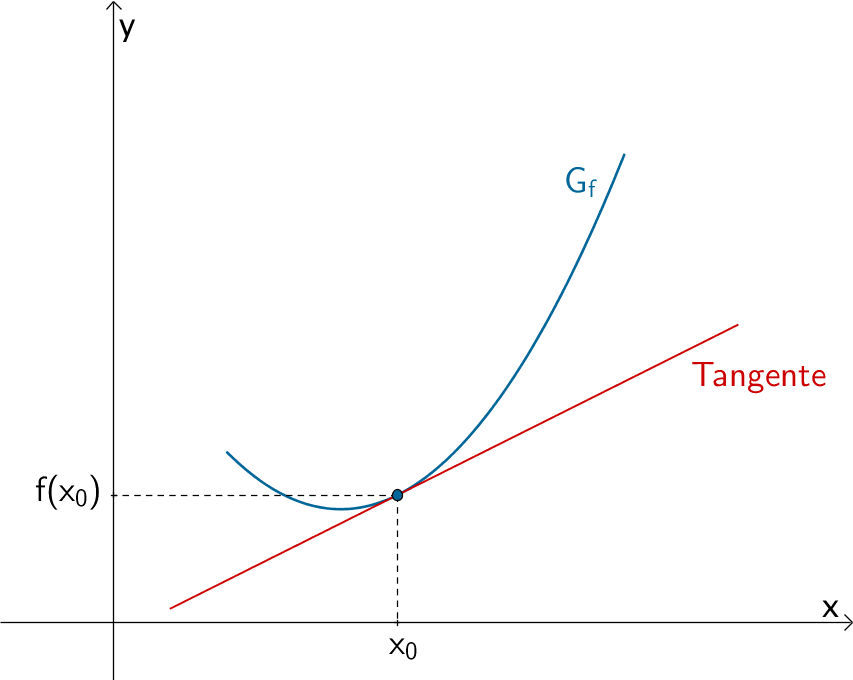
Der Differentialquotient oder die lokale bzw. momentane Änderungsrate \(m_{x_{0}} = \lim \limits_{x \, \to \, x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\) beschreibt den Grenzwert des Differenzenquotienten bei beliebig genauer Annäherung \(x \to x_{0}\) und damit die Steigung der Tangente an den Graphen der Funktion \(f\) an der Stelle \(x_{0}\).
Man nennt den Grenzwert \(m_{x_{0}}\) die Ableitung von \(f\) an der Stelle \(x_{0}\) und schreibt dafür \(f'(x_{0})\).
Differentialquotient oder lokale bzw. momentane Änderungsrate
\[f'(x_{0}) = \lim \limits_{x \, \to \, x_{0}} \frac{f(x) - f(x_{0})}{x - x_{0}}\]
(vgl. Merkhilfe)
Bedeutung im zeitlichen Sachzusammenhang:
Beschreibt eine Funktion den Wert einer Größe in Abhängigkeit von der Zeit, so bedeutet der Differentialquotient die momentane Änderung der Größe pro Zeiteinheit zum betrachteten Zeitpunkt.
Beschreibt beispielsweise eine Funktion die Schadstoffemission eines Schornsteins in Kubikmetern in Abhängigkeit von der Zeit in Minuten, so bedeutet der Differentialquotient in diesem Sachzusammenhang die momentane Emissionsrate in Kubikmeter pro Minute zum betrachteten Zeitpunkt.
Tangentensteigung und Normalensteigung
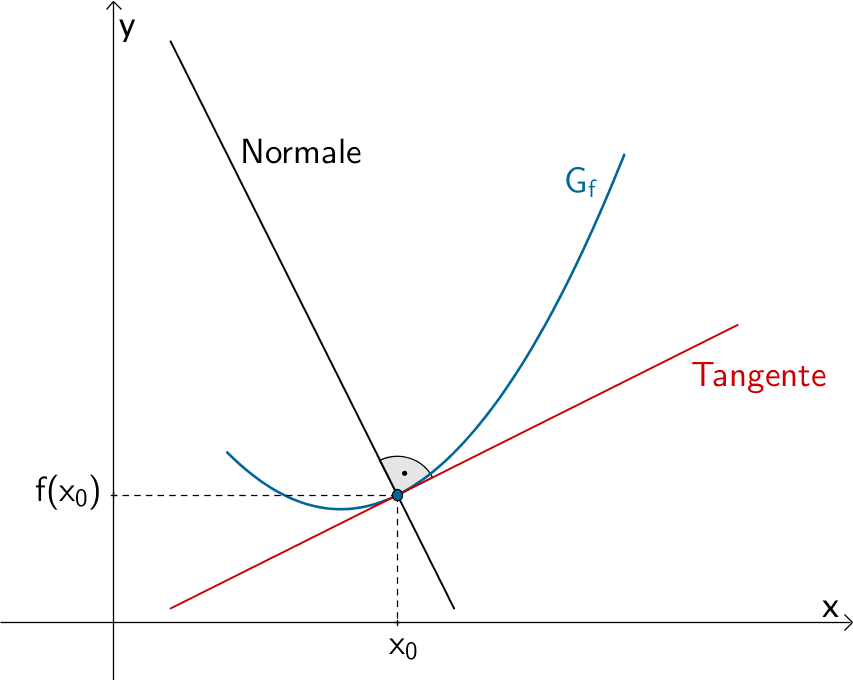
Tangente und Normale des Graphen der Funktion \(f\) im Berührpunkt \((x_{0}|f(x_{0}))\) der Tangente
Die Ableitung \(\boldsymbol{f'}\) einer Funktion \(f\) beschreibt im Punkt \((x_{0}|f(x_{0}))\) die Steigung \(\boldsymbol{m_{T} = f'(x_{0})}\) der Tangente an den Graphen der Funktion \(f\).
Die Normale ist die Lotgerade zur Tangente im Berührpunkt.
Für die Steigungen \(m_{1}\) und \(m_{2}\) zweier zueinander senkrechter Geraden gilt: \(m_{1} \cdot m_{2} = -1\) (vgl. Abiturskript - 1.1.1 Lineare Funktion, Steigung einer Geraden).
Folglich gilt für die Steigung \(m_{T}\) einer Tangente und die Steigung \(m_{N}\) der zugehörigen Normale: \(m_{T} \cdot m_{N} = -1\) bzw. \(m_{N} = -\dfrac{1}{m_{T}}\). Mit \(m_{T} = f'(x_{0})\) ergibt sich somit die Steigung \(m_{N}\) der Normalen zu: \(m_{N} = -\dfrac{1}{f'(x_{0})}\).
Tangentensteigung und Normalensteigung
\[m_{T} = f'(x_{0}) \qquad \quad m_{N} = -\frac{1}{f'(x_{0})}\]
(vgl. Merkhilfe)
Drei klassische Tangentenaufgaben (Tangentenprobleme)
Dieser Punkt behandelt drei gängige Aufgabentypen, welche jeweils unter anderen Voraussetzungen nach der Gleichung einer Tangente fragen.
Für den Ansatz der Gleichung der Tangente \(T\) wird die allgemeine Geradengleichung oder die Tangentengleichung gewählt. Letztere ergibt sich aus der Punkt-Steigung-Form einer Geradengleichung (vgl. Abiturskript - 1.1.1 Lineare Funktion, Geradengleichungen)
Allgemeine Geradengleichung:
\[T \colon y = mx + t\]
Tangentengleichung:
\[T\colon y = f'({x_{0}}) \cdot (x - x_{0}) + f(x_{0})\]
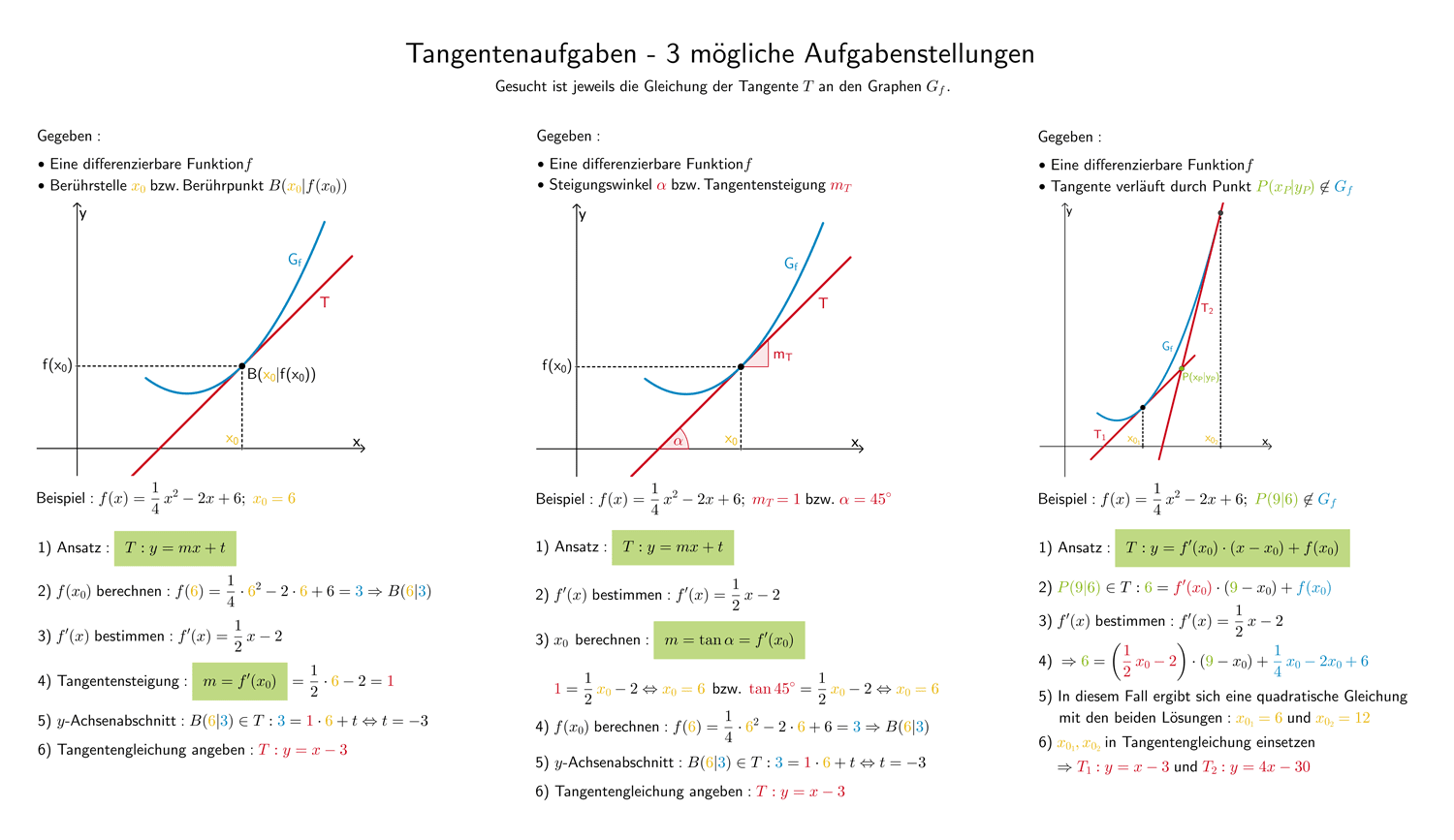
![]() Tangentenaufgaben - 3 mögliche Aufgabenstellungen
Tangentenaufgaben - 3 mögliche Aufgabenstellungen
1. Tangente an \(G_{f}\) an der Stelle \(x_{0}\) bzw. durch Punkt \(B(x_{0}|f(x_{0}))\)
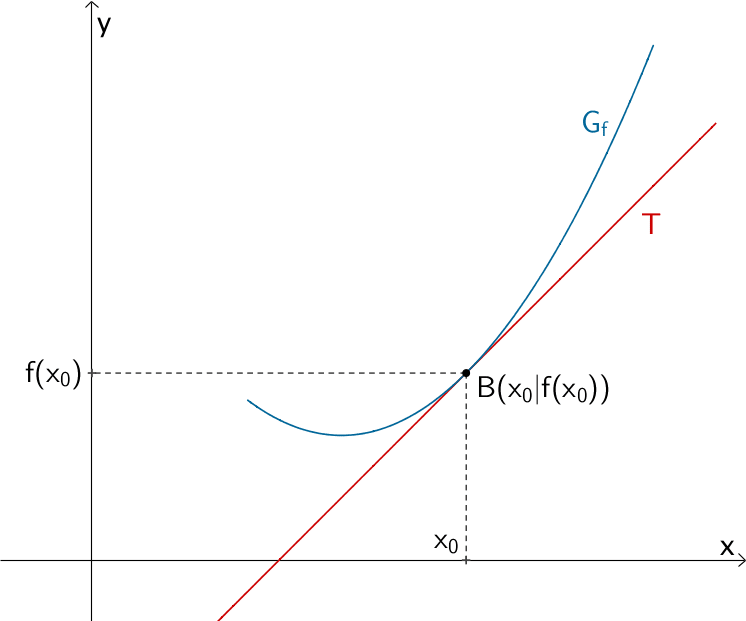
Tangennte \(T\) an den Graphen \(G_{f}\) einer Funktion \(f\) an der Stelle \(x_{0}\) bzw. im Berührpunkt \(B(x_{0}|f_(x_{0}))\)
Gesucht ist die Gleichung der Tangente \(T\).
Gegeben ist die Stelle \(x_{0}\) bzw. der Berührpunkt \(B(x_{0}|f(x_{0}))\) sowie eine Funktion \(f\).
Ansatz mit der allgemeinen Geradengleichung:
Die Steigung \(m_{T}\) der Tangente \(T\) ist gleich dem Wert der Ableitung der Funktion \(f\) an der Stelle \(x_{0}\). Ggf. ist \(f(x_{0})\) zu bestimmen.
Setzt man \(f'(x_{0})\) sowie die Koordinaten von \(B\) in die Gleichung der Tangente \(T\) ein, lässt sich der \(y\)-Achsenabschnitt \(t\) berechnen. Abschließend wird die Gleichung der Tangente angegeben.
\[T \colon y = mx+ t\]
\[m_{T} = f'(x_{0}); \; B(x_{0}|f(x_{0})) \in T\]
\[f(x_{0}) = f'(x_{0}) \cdot x_{0} + t \quad \Longrightarrow \quad t\]
Ansatz mit der Tangentengleichung:
Nachdem \(f'(x_{0})\) und ggf. \(f(x_{0})\) bestimmt wurde, kann die Tangentengleichung vollständig angegeben werden. Durch Umformung erhält man die Gleichung der Tangente in der allgemeinen Form.
\[T\colon y = f'({x_{0}}) \cdot (x - x_{0}) + f(x_{0})\]
Beisspiel:
Gesucht sei die Gleichung der Tangente \(T\) an den Graphen der Funktion \(f \colon \frac{1}{4}x^{2} - 2x + 6\) an der Stelle \(x_{0} = 6\).
Ansatz mit der allgemeinen Geradengleichung:
\[T \colon y = mx + t\]
\[f(x) = \frac{1}{4}x^{2} -2x + 6\]
\(f'(x) = \dfrac{1}{2}x - 2\) (vgl. Abiturskript - 1.5.2 Ableitungsregeln)
\[m_{T} = f'(6) = \frac{1}{2} \cdot 6 - 2 = 1\]
\[f(6) = \frac{1}{4} \cdot 6^{2} - 2 \cdot 6 + 6 = 3\]
\[\Longrightarrow \quad B(6|3)\]
\[\begin{align*}B \in T \colon y &= mx + t \\[0.8em] 3 &= 1 \cdot 6 + t & &| - 6 \\[0.8em] -3 &= t\end{align*}\]
\[\Longrightarrow \quad T \colon y = x - 3\]
Ansatz mit der Tangentengleichung:
\(x_{0} = 6; \; f'(6) = 1; \; f(6) = 3\) (vgl. oben)
\[\begin{align*}T\colon y &= f'({x_{0}}) \cdot (x - x_{0}) + f(x_{0}) \\[0.8em] y &= 1 \cdot (x - 6) + 3 \\[0.8em] y &= x - 3 \end{align*}\]
2. Tangente an \(G_{f}\) mit Steigung \(m\) bzw. Steigungswinkel \(\alpha\)
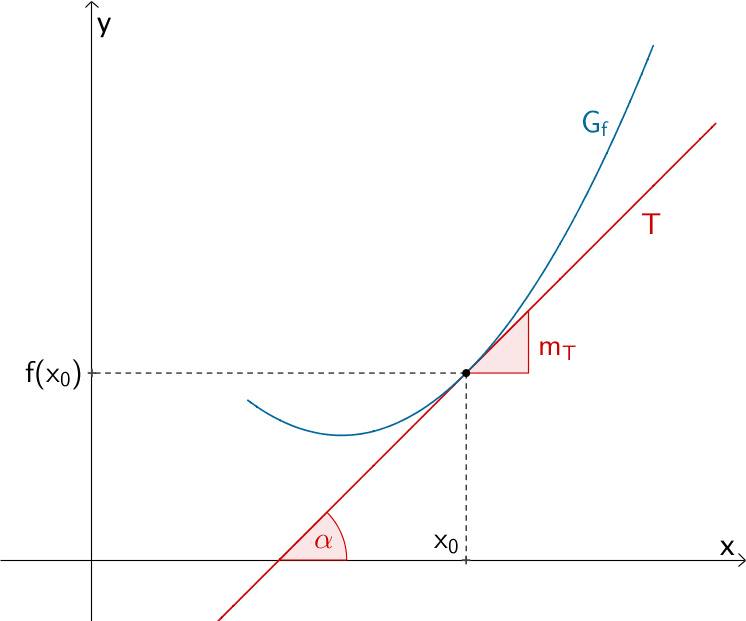
Tangente \(T\) an den Graphen einer Funktion \(f\) mit der Steigung \(m_{T}\) bzw. dem Steigungswinkel \(\alpha\)
Gesucht ist die Gleichung der Tangente \(T\).
Gegeben ist die Steigung \(m_{T}\) bzw. der Steigungswinkel \(\alpha\) sowie eine Funktion \(f\).
Über die Beziehung \(m_{T} = f'(x_{0})\) bestimmt man \(x_{0}\) und damit die Koordinaten des Berührpunkts \(B(x_{0}|f(x_{0}))\). Ist der Steigungswinkel \(\alpha\) der Tangente \(T\) gegeben, kann analog verfahren werden, denn es gilt: \(m_{T} = \tan{\alpha}\) (vgl. Abiturskript - 1.1.1 Lineare Funktion, Steigungswinkel einer Geraden)
\[m_{T} = f'(x_{0}) \quad \Longrightarrow \quad x_{0}, \; B(x_{0}|f(x_{0}))\]
\[\tan{\alpha} = f'(x_{0}) \quad \Longrightarrow \quad x_{0}, \; B(x_{0}|f(x_{0}))\]
Anschließend stellt man die Gleichung der Tangente \(T\) auf, wie unter 1. Tangente an \(G_{f}\) an der Stelle \(x_{0}\) beschrieben.
Beispiel:
Gesucht sei die Gleichung der Tangente \(T\) an den Graphen der Funktion \(f \colon x \mapsto \frac{1}{4}x^{2} - 2x + 6\), welche die Steigung \(m_{T} = 1\) besitzt bzw. den Steigungswinkel \(\alpha = 45^{\circ}\) hat.
\[f(x) = \frac{1}{4}x^{2} - 2x + 6\]
\(f'(x) = \dfrac{1}{2}x - 2\) (vgl. Abiturskript - 1.5.2 Ableitungsregeln)
\[\begin{align*} m_{T} &= f'(x) \\[0.8em] 1 &= \frac{1}{2}x - 2 & &| + 2 \\[0.8em] 3 &= \frac{1}{2}x & &| \cdot 2 \\[0.8em] 6 &= x \end{align*}\]
\[f(6) = \frac{1}{4} \cdot 6^{2} - 2 \cdot 6 + 6 = 3\]
\[\Longrightarrow \quad B(6|3)\]
\[\begin{align*} \tan{\alpha} &= f'(x) \\[0.8em] \tan{45^{\circ}} &= f'(x) \\[0.8em] 1 &= \frac{1}{2}x - 2 & &| + 2 \\[0.8em] 3 &= \frac{1}{2}x & &| \cdot 2 \\[0.8em] 6 &= x \end{align*}\]
\[f(6) = \frac{1}{4} \cdot 6^{2} - 2 \cdot 6 + 6 = 3\]
\[\Longrightarrow \quad B(6|3)\]
Gleichung der Tangente \(T\) aufstellen, wie unter 1. Tangente an \(G_{f}\) an der Stelle \(x_{0}\) beschrieben.
3. Tangente an \(G_{f}\) durch Punkt \(P \notin G_{f}\)
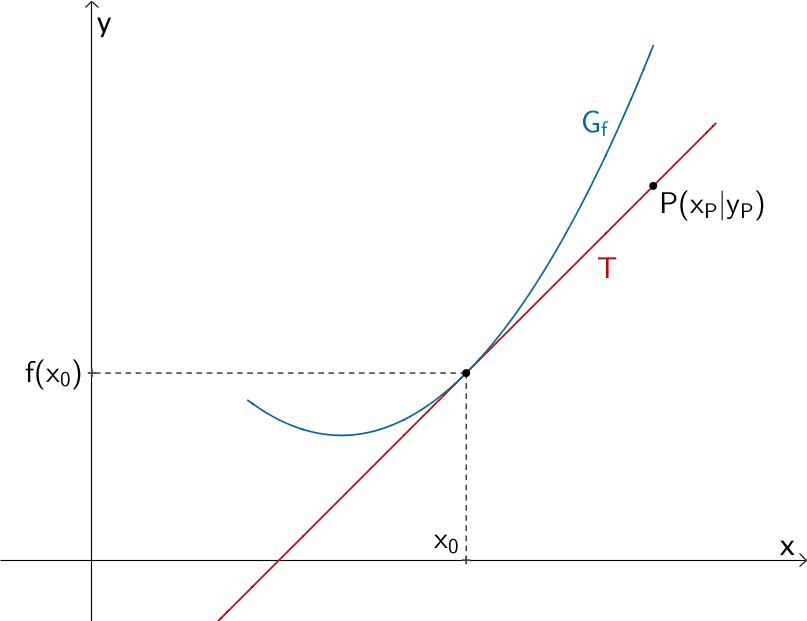
Tangente \(T\) an den Graphen einer Funktion \(f\), welche durch einen Punkt \(P(x_{P}|y_{P})\) verläuft, der nicht der Berührpunkt der Tangente ist.
Gesucht ist die Gleichung der Tangente \(T\).
Gegeben ist ein Punkt \(P \notin G_{f}\) sowie eine Funktion \(f\).
In diesem Fall ist der Ansatz mit der allgemeinen Geradengleichung \(y = mx + t\) nicht zielführend, da weder die Tangentensteigung \(m_{T}\) bekannt ist, noch die Koordinaten des Berührpunkts der Tangente vorliegen, um damit den \(y\)-Achsenabschnitt \(t\) berechnen zu können.
Ansatz mit der Tangentengleichung:
Man setzt die Koordinaten des Punktes \(P\) in die Tangentengleichung ein und erhält eine Gleichung mit der sich die Stelle(n) des Berührpunkts (der Berührpunkte) bestimmen lässt (lassen). Anschließend kann die Gleichung der Tangente aufgestellt werden, wie unter 1. Tangente an \(G_{f}\) an der Stelle \(x_{0}\) beschrieben.
Beispiel:
Gesucht sei die Gleichung der Tangente \(T\) an den Graphen der Funktion \(f \colon x \mapsto \frac{1}{4}x^{2} - 2x + 6\), welche durch den Punkt \(P(9|6) \notin G_{f}\) verläuft.
\[T\colon y = f'({x_{0}}) \cdot (x - x_{0}) + f(x_{0})\]
\[P(9|6)\]
\[f(x) = \frac{1}{4}x^{2} - 2x + 6\]
\(f'(x) = \dfrac{1}{2}x - 2\) (vgl. Abiturskript - 1.5.2 Ableitungsregeln)
Damit ergibt sich:
\[\begin{align*} y_{P} &= f'({x}) \cdot (x_{P} - x) + f(x) \\[0.8em] 6 &= \left( \frac{1}{2}x - 2 \right)(9 - x) + \frac{1}{4}x^{2} - 2x + 6 \\[0.8em] 6 &= \frac{9}{2}x - \frac{1}{2}x^{2} - 18 + 2x + \frac{1}{4}x^{2} - 2x + 6 & &| - 6 \\[0.8em] 0 &= -\frac{1}{4}x^{2} + \frac{9}{2}x - 18 & &| \cdot (-4) \\[0.8em] 0 &= x^{2} - 18x + 72 \end{align*}\]
Lösungsformel für quadratische Gleichungen anwenden (vgl. Abiturskript - 1.1.2 Quadratische Funktion, Lösungsformel für quadratische Gleichungen, vgl. Merkhilfe):
\[\begin{align*} x_{1,2} &= \frac{18 \pm \sqrt{(-18)^{2} - 4 \cdot 1 \cdot 72}}{2 \cdot 1} \\[0.8em] &= \frac{18 \pm \sqrt{36}}{2} \\[0.8em] &= 9 \pm 3 \end{align*}\]
\[x_{1} = 6; \; x_{2} = 12\]
Es gibt zwei Tangenten an den Graphen \(G_{f}\) der Funktion \(f\), welche durch den Punkt \(P(9|6)\) verlaufen. Sie berühren \(G_{f}\) an den Stellen \(x_{1} = 6\) bzw. \(x_{2} = 12\). Die Gleichungen der beiden Tangenten lassen sich aufstellen, wie unter 1. Tangente an \(G_{f}\) an der Stelle \(x_{0}\) beschrieben.
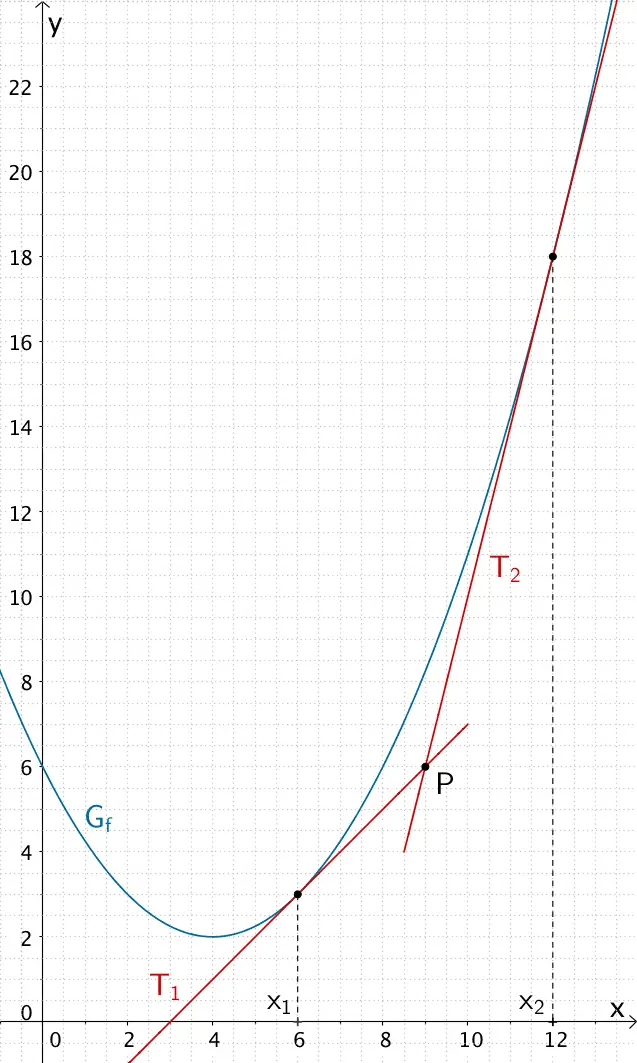
Tangente \(T_{1}\) und Tangente \(T_{2}\) an den Graphen \(G_{f}\) der Funktion \(f \colon x \mapsto \frac{1}{4}x^{2} - 2x + 6\), welche durch den Punkt \(P(9|6) \notin G_{f}\) verlaufen.
Differenzierbarkeit
Eine Funktion \(f\) heißt an der Stelle \(x_{0}\) differenzierbar (ableitbar), wenn der Differentialquotient \(m_{x_{0}} = \lim \limits_{x \, \to \, x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\) an der Stelle \(x_{0}\) existiert.
Das bedeutet, dass der Differentialquotient sowohl bei linksseitiger Annäherung \(x \to x_{0}^{-}\) als auch bei rechtsseitiger Annäherung \(x \to x_{0}^{+}\) denselben Grenzwert annehmen muss, damit eine Funktion \(f\) an der Stelle \(x_{0}\) differenzierbar ist.
Beispiel:
Die Betragsfunktion \(f \colon x \mapsto \vert x \vert\) ist an der Stelle \(x = 0\) nicht differenzierbar (vgl. Abiturskript - 1.1.5 Betragsfunktion).
Nachweis:
\[ f(x) = \vert x \vert = \begin{cases} -x &\text{für} \quad x < 0 \\[0.8em] \hspace{13px}x &\text{für} \quad x \geq 0 \end{cases}\]
Damit ergibt sich:
\[\lim \limits_{x \, \to \, 0^{-}} \frac{f(x) - f(0)}{x - 0} = \lim \limits_{x \, \to \, 0^{-}} \frac{-x - 0}{x - 0} = -1\]
\[\lim \limits_{x \, \to \, 0^{+}} \frac{f(x) - f(0)}{x - 0} = \lim \limits_{x \, \to \, 0^{+}} \frac{x - 0}{x - 0} = 1\]
Da der linksseitige und der rechtsseitige Grenzwert verschieden sind, existiert der Grenzwert \(\lim \limits_{x \, \to \, 0} \dfrac{f(x) - f(0)}{x - 0}\) nicht und die Funktion \(f \colon x \mapsto \vert x \vert\) ist somit an der Stelle \(x = 0\) nicht differenzierbar.
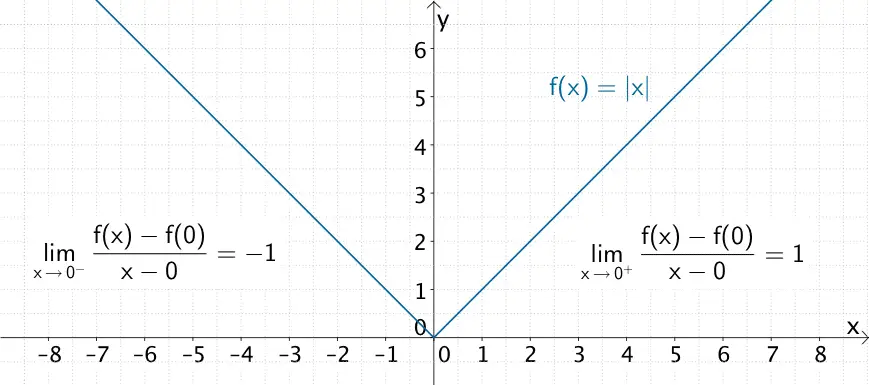
Graph der an der Stelle \(x = 0\) nicht differenzierbaren Betragsfunktion \(f \colon x \mapsto \vert x \vert\)
Graphische Interpretation der Differenzierbarkeit:
Ein Funktion \(f\) ist an der Stelle \(x_{0}\) differenzierbar, wenn der Graph der Funktion \(f\) an der Stelle \(x_{0}\) keinen „Knick" oder „Sprung" aufweist.
Beispielaufgabe
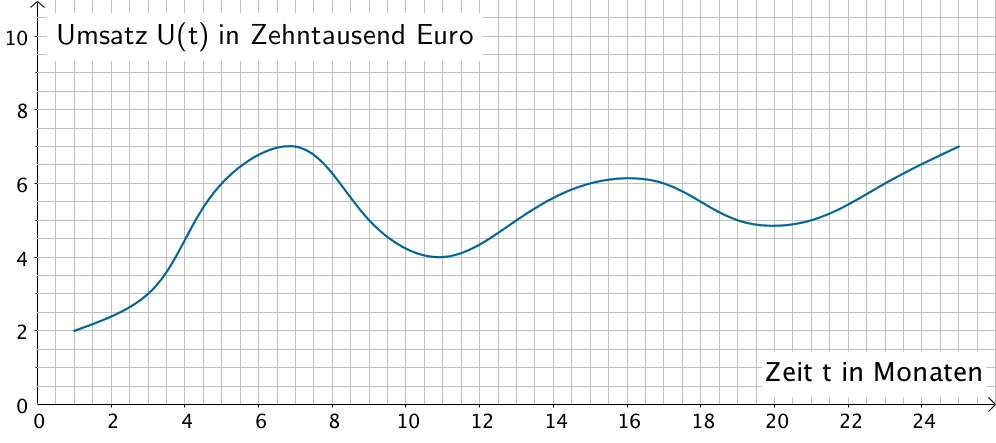
Die Abbildung zeigt für eine Zeitspanne von zwei Jahren den Graphen der Umsatzentwicklung für den Verkauf eines Sportartikels ab Markeinführung am 1. Januar 2014. Die Funktion \(t \mapsto U(t)\) beschreibt für \(t \in ]1;25[\) (\(t\) in Monaten) die Umsatzentwicklung.
Bestimmen Sie mithilfe der Abbildung für die Zeit vom 1. Dezember 2014 bis zum 1. Mai 2015 den mittleren monatlichen Umsatz. Geben Sie mit einer Genauigkeit von einem Monat den kalendarischen Zeitpunkt an, zu dem der Umsatz am stärksten zunahm und begründen Sie Ihre Wahl. Berechnen Sie mithilfe der Abbildung einen Näherungswert für die stärkste Umsatzzunahme.
Mittlerer monatlicher Umsatz vom 1. Dezember 2014 bis 1. Mai 2015
Zunächst wird das zu betrachtende Zeitintervall für bestimmt.
1. Januar 2014 entspricht \(t = 1\)
1. Dezember 2014 entspricht \(t = 1 + 11 = 12\)
1. Mai 2015 entspricht \(t = 1 + 16 = 17\)
\(\Longrightarrow \quad t \in [12;17]\) in Monaten
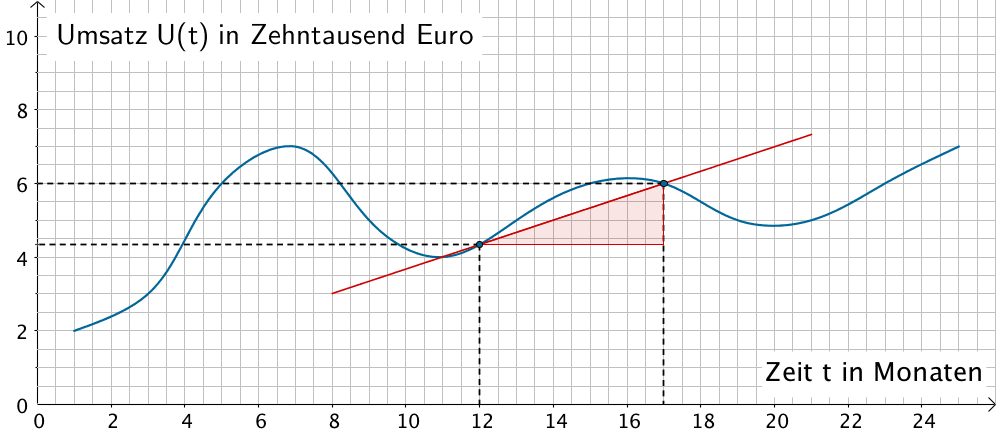
Der Mittlere monatliche Umsatz vom 1. Dezember 2014 bis 1. Mai 2015 entspricht der mittleren Änderungsrate des Umsatzes \(U(t)\) für \(t \in [12;17]\). Sie errechnet sich als die Steigung der Sekante durch die Punkte \((12|U(12))\) und \((17|U(17))\).
Im Rahmen der Ablesegenauigkeit entnimmt man der Abbildung die Umsatzwerte vom 1. Dezember 2014 und vom 1. Mai 2015.
Umsatz vom 1. Dezember 2014 in Euro: \(U(12) \approx 4{,}4 \cdot 10000 = 44000\)
Umsatz vom 1. Mai 2015 in Euro: \(U(17) \approx 6{,}0 \cdot 10000 = 60000\)
\[m_{s} = \frac{U(17) - U(12)}{17 - 12} = \frac{60000 - 44000}{17 - 12} = \frac{16000}{5} = 3200\]
In der Zeit vom 1. Dezember 2014 bis 1. Mai 2015 erzielte der Verkauf des Sportartikels einen mittleren Umsatz von 3200 € pro Monat.
Zeitpunkt der stärksten Umsatzzunahme
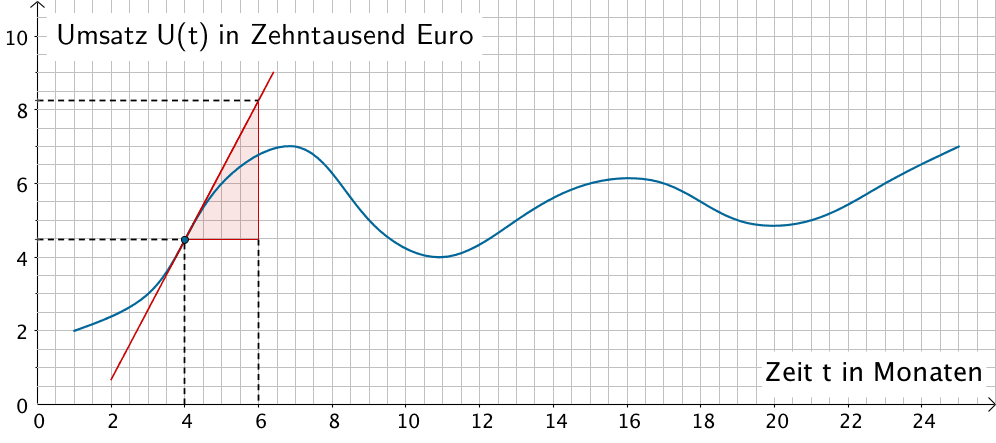
Im Intervall \(t \in [2;6]\) zeigt die Umsatzentwicklung einen Zuwachs des Umsatzes. Zum Zeitpunkt \(t = 4\) steigt der Graph der Funktion \(U\) am stärksten an. Die Steigung der Tangente im Punkt \((4|U(4))\) entspricht der stärksten Zunahme des Umsatzes.
Der Zeitpunkt \(t = 4\) entspricht dem kalendarischen Zeitpunkt 1. April 2014.
Näherungswert für die stärkste Umsatzzunahme
Zunächst wählt man für die Tangente im Punkt \((4|U(4))\) ein geeignetes Steigungsdreieck. Anschließend entnimmt man der Abbildung mithilfe des Steigungsdreiecks die Koordinaten zweier Punkte zur Bestimmung der Tangentensteigung. Im Falle des eingezeichneten Steigungsdreiecks lauten die Koordinaten \((4|45000)\) und \((6|83000)\) (im Rahmen der Ablesegenauigkeit).
Damit ergibt sich die Steigung der Tangente zu:
\[m_{T} = \frac{83000 - 45000}{6 - 2} = \frac{38000}{2} = 19000\]
Zum 1. April 2014 war die Zunahme des Umsatzes für den Verkauf des Sportartikels mit ca. 19000 € pro Monat am stärksten.