Eine Funktion \(f \colon x \mapsto f(x)\) mit der Definitionsmenge \(D_{f}\) und der Wertemenge \(W_{f}\) heißt umkehrbar, falls es zu jedem \(y \in W_{f}\) genau ein \(x \in D_{f}\) mit \(f(x) = y\) gibt.
Ist eine Funktion umkehrbar, so ist die umgekehrte Zuordnung eine Funktion, die als Umkehrfunktion von \(f\) mit \(f^{-1}\) bezeichnet wird.
Kriterium für die Umkehrbarkeit einer Funktion
Am Verlauf des Graphen einer Funktion lässt sich bereits erkennen, ob eine Funktion umkehrbar ist. Wenn jede Parallele zur \(x\)-Achse, den Graphen der Funktion höchstens einmal schneidet, ist die Funktion umkehrbar. Diese Bedingung erfüllen alle streng monoton verlaufenden Funktionen.
Ist eine Funktion \(f\) auf Ihrem Definitionsbereich bzw. einem Teilintervall des Definitionsbereichs nur streng monoton zunehmend oder nur streng monoton abnehmend, so ist sie dort umkehrbar.
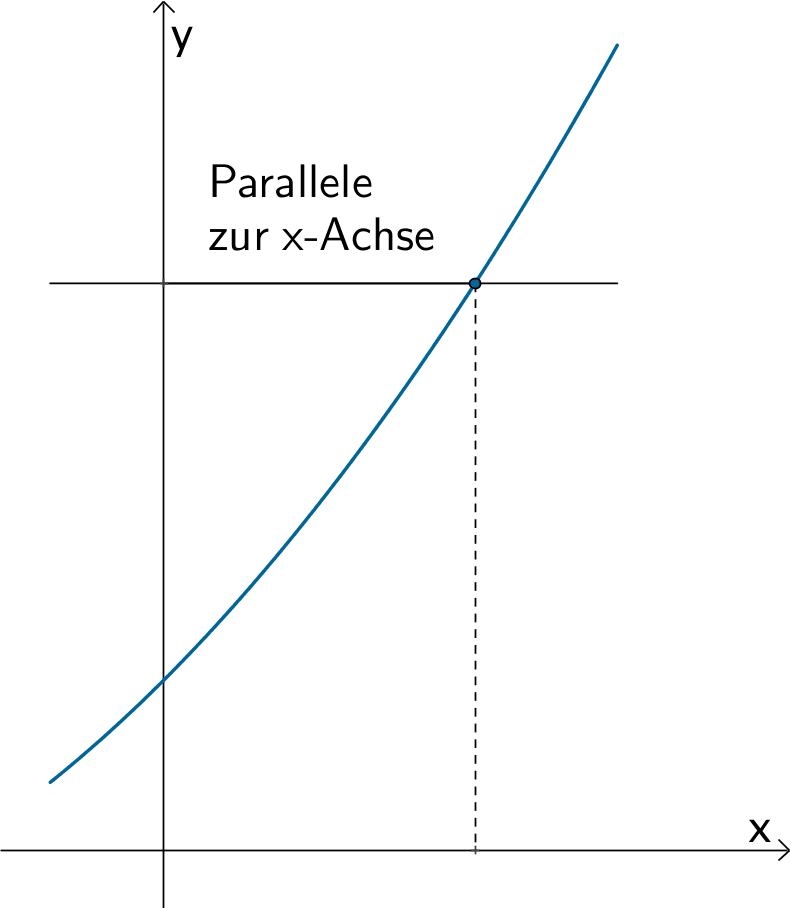
Graph einer umkehrbaren Funktion
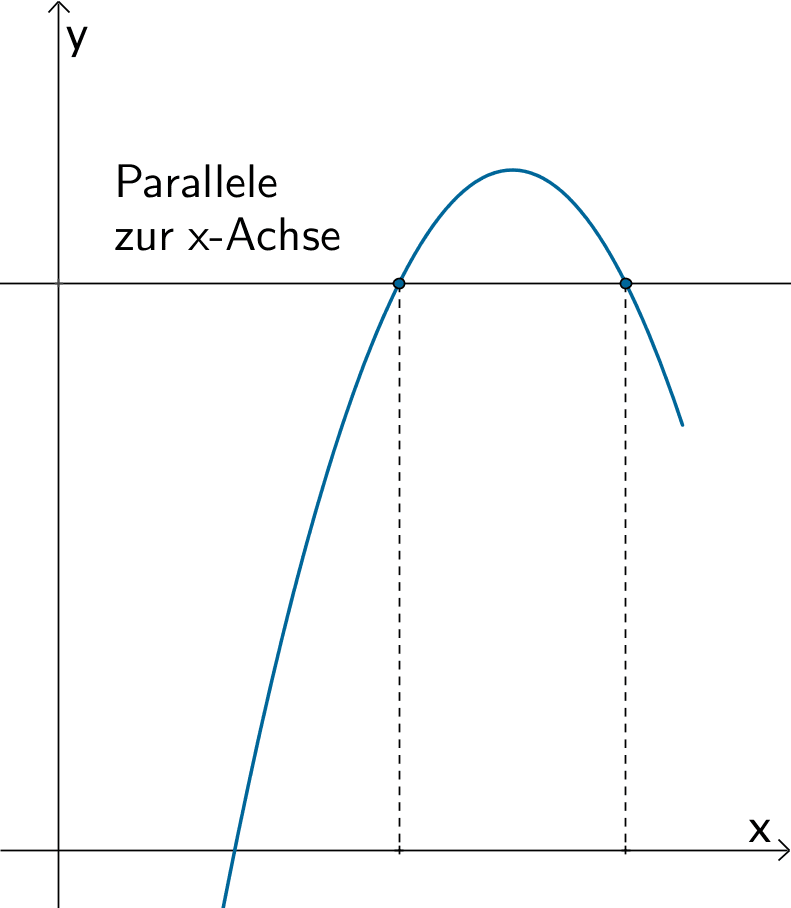
Graph einer nicht umkehrbaren Funktion
Die Umkehrbarkeit einer Funktion lässt sich demnach mithilfe des Monotoniekriteriums untersuchen (vgl. Abiturskript - 1.5.3 Monotonieverhalten, Extrem- und Terrassenpunkte). Gilt \(f'(x) < 0\) oder \(f'(x) > 0\) in einem Intervall \(I\), so ist die Funktion \(f\) im Intervall \(I\) umkehrbar.
Bestimmung des Funktionsterms \(f^{-1}(x)\) einer Umkehrfunktion
Um den Funktionsterm \(f^{-1}(x)\) der Umkehrfunktion einer Funktion \(f\) zu bestimmen, löst man zunächst die Gleichung \(y = f(x)\) nach der Variablen \(x\) auf. Anschließend tauscht man die Variablen \(x\) und \(y\), wobei nun \(y = f^{-1}(x)\) gilt. Die beiden Schritte können auch in umgekehrter Reihenfolge ausgeführt werden.
Bei der Umkehrung einer Funktion werden der Definitionsbereich und der Wertebereich miteinander vertauscht. Es gilt: \(D_{f^{-1}} = W_{f}\) und \(W_{f^{-1}} = D_{f}\).
Beispiel:
\[f(x) = \sqrt{x - 3}; \; D_{f} = [3;+\infty[, \; W_{f} = \mathbb R^{+}_{0}\]
1. Die Gleichung \(y = f(x)\) nach \(x\) auflösen:
\[\begin{align*}y &= f(x) \\[0.8em] y &= \sqrt{x - 3} & &| \;(\dots)^{2}\enspace \text{(Quadrieren)} \\[0.8em] y^{2} &= x - 3 & &| + 3 \\[0.8em] y^{2} + 3&= x \end{align*}\]
2. Variablen \(x\) und \(y\) tauschen:
\[y = x^{2} + 3\]
\[\Longrightarrow \quad f^{-1}(x) = x^{2} + 3; \; D_{f^{-1}} = W_{f} = \mathbb R^{+}_{0}, \; W_{f^{-1}} = D_{f} = [3;+\infty[\]
oder
1. Variablen \(x\) und \(y\) tauschen:
\[y = f(x) \quad \longrightarrow \quad x = f(y)\]
2. Die Gleichung \(x = f(y)\) nach \(y\) auflösen:
\[\begin{align*} x &= f(y) \\[0.8em] x &= \sqrt{y - 3} & &| \; (\dots)^{2}\enspace \text{(Quadrieren)} \\[0.8em] x^{2} &= y - 3 & &| + 3 \\[0.8em] x^{2} + 3 &= y \end{align*}\]
\[\Longrightarrow \quad f^{-1}(x) = x^{2} + 3; \; D_{f^{-1}} = W_{f} = \mathbb R^{+}_{0}, \; W_{f^{-1}} = D_{f} = [3;+\infty[\]
Funktionsgraph einer Umkehrfunktion
Der Graph einer Funktion \(f\) und der Graph der Umkehrfunktion \(f^{-1}\) verlaufen achsensymmetrisch zur Gerade \(y = x\) (Winkelhalbierende des I. und III. Quadranten). Man erhält den Graphen einer Umkehrfunktion \(f^{-1}\), indem man den Graphen der zugehörigen Funktion \(f\) an der Geraden \(y = x\) spiegelt.
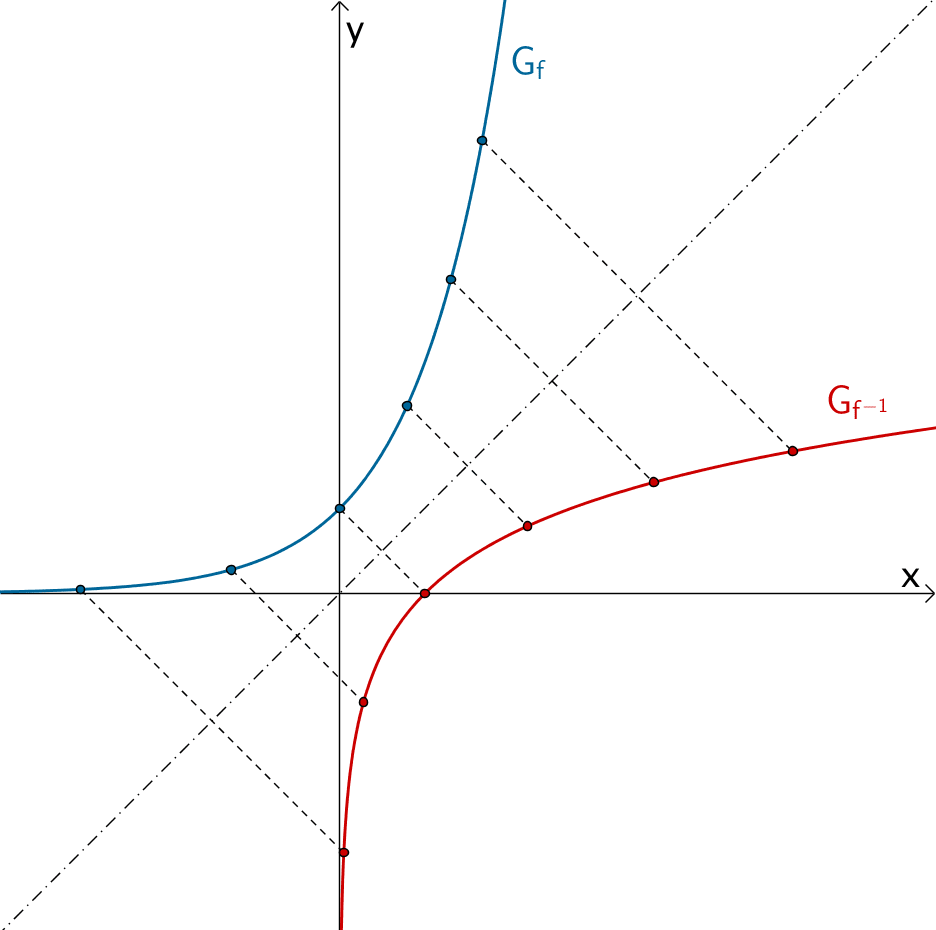
Beispiel: Der Graph der Umkehrfunktion \(f^{-1} \colon x \mapsto \ln x\) geht durch Spiegelung des Graphen der Funktion \(f \colon x \mapsto e^{x}\) an der Geraden \(y = x\) hervor (vgl. Abiturskript - 1.3.1 Natürliche Exponetial- und Logarithmusfunktion, Eigenschaften und Rechenregeln).
Beispielaufgabe
Gegeben sei die in \(\mathbb R\) definierte Funktion \(f \colon x \mapsto 5 \cdot e^{x - 4}\).
Geben Sie den Wertebereich der Funktion \(f\) an. Bestätigen Sie durch Rechnung, dass die Funktion \(f\) in \(\mathbb R\) umkehrbar ist. Bestimmen Sie den Funktionsterm der Umkehrfunktion von \(f\) und geben Sie den Definitionsbereich und den Wertebereich der Umkehrfunktion von \(f\) an. Skizzieren Sie den Graphen der Funktion \(f\) und den Graphen der Umkehrfunktion von \(f\) für \(x \in [-1;5]\) in ein gemeinsames Koordinatensystem.
\[f(x) = 5 \cdot e^{x - 4}\,; \enspace D_{f} = \mathbb R\]
Wertebereich der Funktion \(f\)
Die Natürliche Exponentialfunktion \(x \mapsto e^{x}\) hat den Wertebereich \(W = \mathbb R^{+}\) (vgl. Abiturskript - 1.3.1 Natürliche Exponetial- und Logarithmusfunktion, Eigenschaften und Rechenregeln). Die Funktion \(f\) ist gegenüber der Natürlichen Exponentialfunktion um 4 Einheiten in Richtung der positiven \(x\)-Achse verschoben und um den Faktor 5 in \(y\)-Richtung gestreckt (vgl. Abiturskript - 1.1.7 Entwicklung von Funktionen). Der Wertebereich der Funktion \(f\) verändert sich dadurch nicht.
\[W_{f} = \mathbb R^{+}\]
Nachweis, dass die Funktion \(f\) in \(\mathbb R\) umkehrbar ist
Die Funktion \(f\) ist in \(\mathbb R\) umkehrbar, wenn sie in \(\mathbb R\) entweder nur streng monoton fallend oder nur streng monoton steigend ist, also wenn für \(x \in \mathbb R\) entweder \(f'(x) < 0\) oder \(f'(x) > 0\) gilt (vgl. 1.5.3 Monotonieverhalten, Extrem- und Terrassenpunkte).
Erste Ableitung \(f'\) bilden:
Die erste Ableitung \(f'\) der Funktion \(f\) kann mithilfe der Faktorregel, der Ableitung der Natürlichen Exponentialfunktion und der Kettenregel formuliert werden (vgl. Abiturskript - 1.5.2 Ableitungsregeln).
\[f(x) = 5 \cdot e^{x - 4}\]
\[f'(x) = 5 \cdot e^{x - 4} \cdot 1 = 5 \cdot \underbrace{e^{x-4}}_{>\,0}\]
\(\Longrightarrow \quad f'(x) > 0\) für \(x \in \mathbb R\)
\(\Longrightarrow \quad\) Der Graph \(G_{f}\) steigt für \(x \in \mathbb R\) streng monoton.
\(\Longrightarrow \quad\) Die Funktion \(f\) ist in \(\mathbb R\) umkehrbar.
Bestimmung des Funktionsterms der Umkehrfunktion
1. Die Gleichung \(y = f(x)\) nach \(x\) auflösen:
\[\begin{align*} y &= f(x) \\[0.8em] y &= 5 \cdot e^{x - 4} & &| \; \ln \;\text{(Logarithmieren)}\\[0.8em] \ln{y} &= \ln{\left( 5 \cdot e^{x - 4} \right)} & &| \; \log_{a}(u \cdot v) = \log_{a}{u} + \log_{a}{v} \\[0.8em] \ln{y} &= \ln{5} + \ln{\left( e^{x - 4} \right)} & &| \; \ln{e^{x}} = x \\[0.8em] \ln{y} &= \ln{5} + x - 4 & &| - \ln{5} + 4 \\[0.8em] \ln{y} - \ln{5} + 4 &= x & &| \; \log_{a}{u} - \log_{a}{v} = \log_{a}\left( \frac{u}{v} \right) \\[0.8em] \ln{\left( \frac{y}{5} \right)} + 4 &= x \end{align*}\]
2. Variablen \(x\) und \(y\) tauschen:
\[y = \ln{\left( \frac{x}{5} \right)} + 4\]
\[\Longrightarrow \quad f^{-1}(x) = \ln{\left( \frac{x}{5} \right)} + 4; \; D_{f^{-1}} = W_{f} = \mathbb R^{+}, \; W_{f^{-1}} = D_{f} = \mathbb R\]
oder
1. Variablen \(x\) und \(y\) tauschen:
\[y = f(x) \quad \longrightarrow \quad x = f(y)\]
2. Die Gleichung \(x = f(y)\) nach \(y\) auflösen:
\[\begin{align*} x &= f(y) \\[0.8em] x &= 5 \cdot e^{y - 4} & &| \; \ln \;\text{(Logarithmieren)}\\[0.8em] \ln{x} &= \ln{\left( 5 \cdot e^{y - 4} \right)} & &| \; \log_{a}(u \cdot v) = \log_{a}{u} + \log_{a}{v} \\[0.8em] \ln{x} &= \ln{5} + \ln{\left( e^{y - 4} \right)} & &| \; \ln{e^{x}} = x \\[0.8em] \ln{x} &= \ln{5} + y - 4 & &| - \ln{5} + 4 \\[0.8em] \ln{x} - \ln{5} + 4 &= y & &| \; \log_{a}{u} - \log_{a}{v} = \log_{a}\left( \frac{u}{v} \right) \\[0.8em] \ln{\left( \frac{x}{5} \right)} + 4 &= y \end{align*}\]
\[\Longrightarrow \quad f^{-1}(x) = \ln{\left( \frac{x}{5} \right)} + 4; \; D_{f^{-1}} = W_{f} = \mathbb R^{+}, \; W_{f^{-1}} = D_{f} = \mathbb R\]
Skizzieren von \(G_{f}\) und \(G_{f^{-1}}\) für \(x \in [-1;5]\)
Man skizziert zunächst den Graphen der Funktion \(f\). Den Graphen der Umkehrfunktion \(f^{-1}\) erhält man durch Spiegelung von \(G_{f}\) an der Geraden \(y = x\).
Wie bereits erwähnt, ist der Graph der Funktion \(f\) gegenüber dem Graphen der Natürlichen Exponnetialfunktion \(x \mapsto e^{x}\) um 4 Einheiten in Richtung der positiven \(x\)-Achse verschoben und um den Faktor \(5\) in \(y\)-Richtung gestreckt. Der Graph der Natürlichen Exponetialfunktion verläuft durch den Punkt \((0|1)\). Also verläuft der Graph der Funktion \(f\) durch den Punkt \((4|5)\). Diese Information reicht aus, um den Graphen der Funktion \(f\) ausgehend vom Graphen der Natürlichen Exponentialfunktion zu skizzieren (vgl. Abiturskript - 1.3.1 Natürliche Exponetial- und Logarithmusfunktion, Eigenschaften und Rechenregeln).
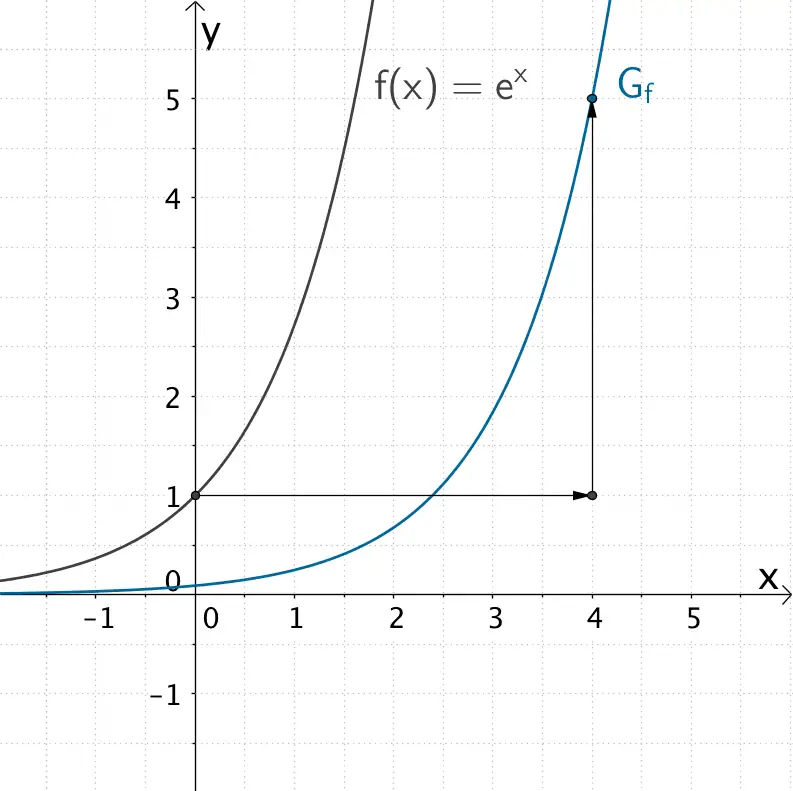
Entstehung des Graphen der Funktion \(f\)
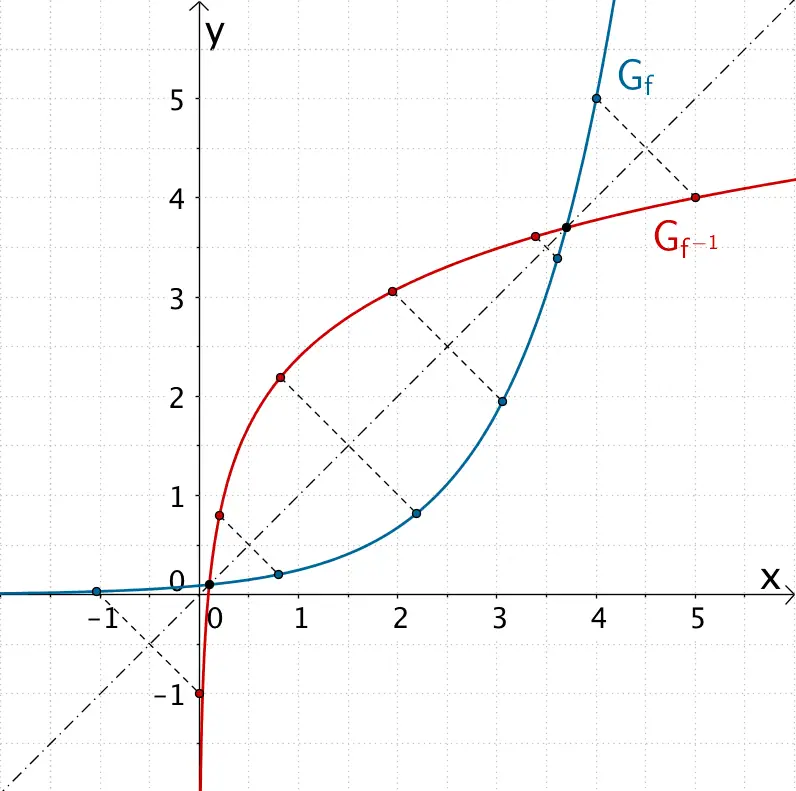
Graph der Funktion \(f \colon x \mapsto 5 \cdot e^{x - 4}\) und Graph der Umkehrfunktion \(f^{-1} \colon x \mapsto \ln{\left( \frac{x}{5} \right)} + 4\)

