Extremwertaufgaben fragen nach der Voraussetzung, unter der eine genannte Größe einen Extremwert erreicht. Meist ist zusätzlich der Extremwert zu berechnen. In der Regel muss eine Zielfunktion formuliert werden, welche die jeweilige Größe in Abhängigkeit einer Variablen beschreibt. Oftmals bedarf es einer Nebenbedingung, um den Funktionsterm der Zielfunktion in Abhängigkeit von nur einer Variablen aufstellen zu können.
Anschließend wird die Zielfunktion mit den Mitteln der Differentialrechnung auf Extremstellen hin untersucht (vgl. Abiturskript - 1.5.3 Monotonieverhalten, Extrem- und Terrassenpunkte). Je nach Aufgabenstellung ist es ggf. erforderlich, auch die Art der Extremstelle nachzuweisen.
Von besonderer Bedeutung ist der Definitionsbereich der Zielfunktion. Abhängig vom Sachzusammenhang der zu beschreibenden Größe, ist der Definitionsbereich der Zielfunktion für gewöhnlich eingeschränkt. Mithilfe der Differentialrechnung lassen sich relative Extremstellen innerhalb des Definitionsbereichs untersuchen. Die Ränder des Definitionsbereichs werden nicht erfasst, da die Zielfunktion an den Definitionsrändern nicht differenzierbar ist. Der Differentialquotient (Die Ableitung) der Zielfunktion existiert an den Definitionsrändern nicht, auch wenn die Zielfunktion selbst dort definiert ist (vgl. Abiturskript - 1.5.1 Die Ableitung, Differenzierbarkeit). Das bedeutet, dass die Werte, welche die Zielfunktion an den Definitionsrändern annehmen kann, mit dem relativen Extremwert verglichen werden müssen, um mögliche Randextrema zu berücksichtigen.
Vorgehensweise für Extremwertaufgaben
- 1. Zielfunktion formulieren (ggf. mithilfe einer Nebenbedingung) und einen im Sachzusammenhang sinnvollen Definitionsbereich festlegen.
- 2. Zielfunktion auf relative Extremstelle(n) hin untersuchen und ggf. die Art der Extremstelle(n) nachweisen.
- 3. Relative(n) Extremwert(e) mit den Funktionswerten der Zielfunktion an den Definitionsrändern vergleichen.
Beispiel:
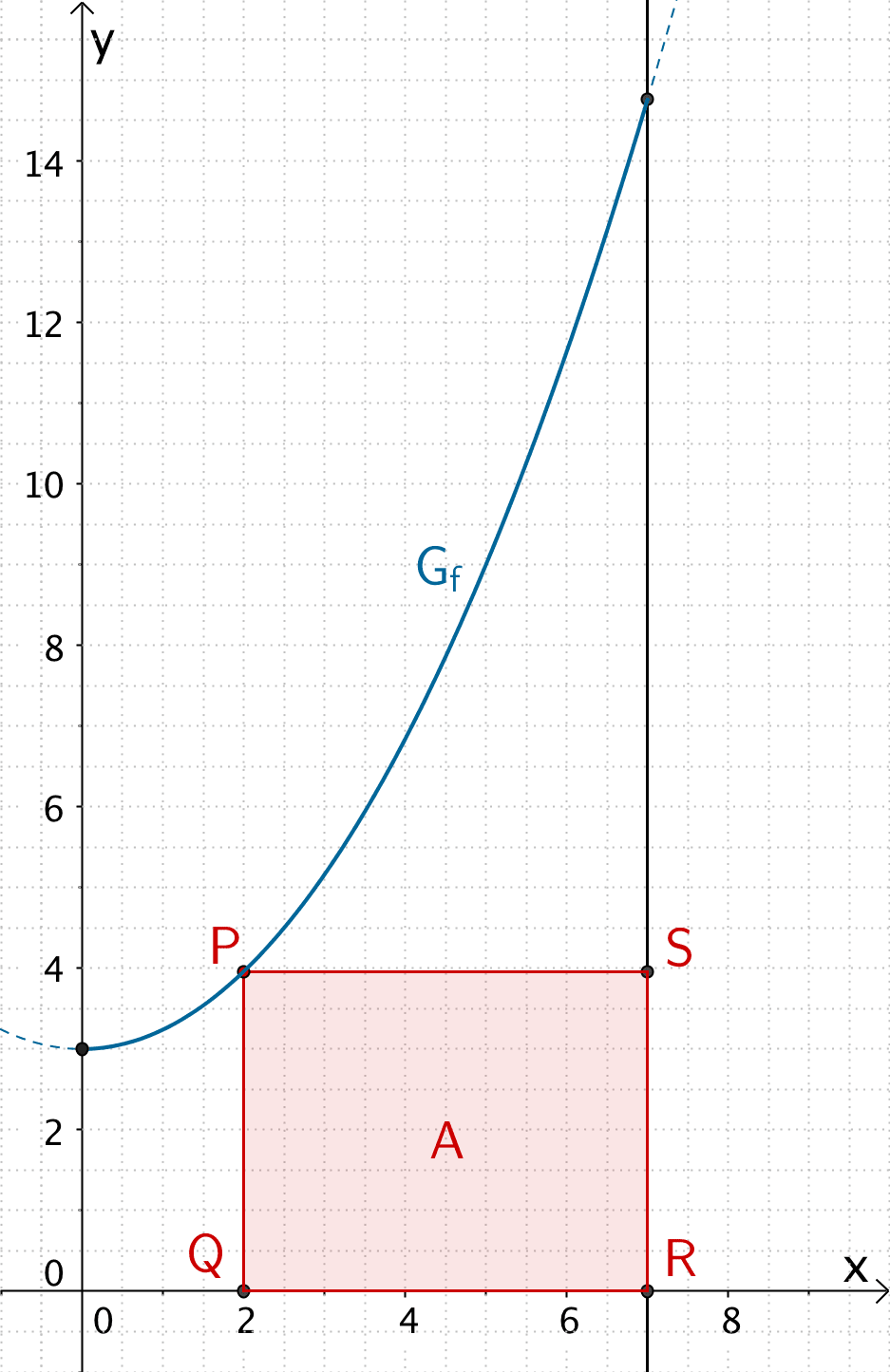
Der Punkt \(P(x|y)\) liegt für \(x_P \in [0;7]\) auf dem Graphen \(G_{f}\) der Funktion \(f \colon x \mapsto 0{,}24x^{2}+3\). Er ist Eckpunkt von Rechtecken \(QRSP\) mit dem Flächeninhalt \(A\). Die Seite \([QR]\) der Rechtecke \(QRSP\) liegt auf der \(x\)-Achse. Die Seite \([RS]\) liegt auf der Geraden mit der Gleichung \(x = 7\) (vgl. Abbildung).
Bestimmen Sie die Koordinaten des Punktes \(P\) sodass der Flächeninhalt \(A\) extremal ist und berechnen Sie den Extremwert des Flächeninhalts.
1. Zielfunktion formulieren:
Die Zielfunktion beschreibt den Flächeninhalt \(A\) der Rechtecke \(QRSP\), in Abhängigkeit von der Lage des Punktes \(P\). Da der Punkt \(P\) auf dem Graphen der Funktion \(f\) liegt, verändert sich der Flächeninhalt \(A\) in Abhängigkeit von der \(x\)-Koordinate des Punktes \(P\).
\[\begin{align*}A(x) &= \overline{QR}(x) \cdot \overline{QP}(x) \\[0.8em] &= (7 - x) \cdot f(x) \\[0.8em] &= (7 - x) \cdot (0{,}24x^{2} + 3) \\[0.8em] &= -0{,}24x^{3} + 1{,}68x^{2} - 3x + 21 \end{align*}\]
Sinnvoller Definitionsbereich für \(A(x)\):
Die Zielfunktion beschreibt den Flächeninhalt von Rechtecken. Für die Punkte \(P(x|y)\) gilt \(x \in [0;7]\). Für \(x = 0\) liegt \(P\) auf der \(y\)-Achse und es existiert ein Rechteck \(QRSP\), für \(x = 7\) liegt \(P\) auf der Geraden x = 7 und es existiert kein Rechteck mehr.
\[\Longrightarrow \quad D_{A} = [0;7[\]
2. Zielfunktion \(A(x)\) auf relative Extremstellen hin untersuchen und deren Art nachweisen:
Da die Aufgabenstellung die Art des Extremwerts offen lässt, erfolgt zusätzlich der Nachweis der Art der Extremstelle. Es ist allerdings offensichtlich, dass es sich nur um einen maximalen Flächeninhalt des Rechtecks \(QRSP\) handeln kann, da der Flächeninhalt für \(x \to 7\) beliebig klein wird.
Notwendige Bedingung für eine Extremstelle von \(A(x)\):
\[A'(x) \overset{!}{=} 0\]
Erste Ableitung \(A'\) bilden:
Die erste Ableitung \(A'\) der Funktion \(A\) kann mithilfe der Faktorregel, der Summenregel und der Potenzregel formuliert werden (vgl. Abiturskript - 1.5.2 Ableitungsregeln).
\[A(x) = -0{,}24x^{3} + 1{,}68x^{2} - 3x + 21\]
\[\begin{align*} A'(x) &= -0{,}24 \cdot 3x^{2} + 1{,}68 \cdot 2x -3 \\[0.8em] &= -0{,}72x^{2} + 3{,}36x - 3 \end{align*}\]
Nullstellen von \(A'\) ermitteln:
\[-0{,}72x^{2} + 3{,}36x - 3 = 0\]
Die Nullstellen der ersten Ableitung \(A'(x)\) werden mithilfe der Lösungsformel für quadratische Gleichungen bestimmt (vgl. Abiturskript - 1.1.2 Quadratische Funktion, Nullstellen).
\[\begin{align*}x_{1,2} &= \frac{-3{,}36 \pm \sqrt{3{,}36^{2} - 4 \cdot (-0{,}72) \cdot (-3)}}{2 \cdot (-0{,}72)} \\[0.8em] &= \frac{-3{,}36 \pm \sqrt{2{,}6496}}{-1{,}44} \end{align*}\]
\[x_{1} \approx 1{,}20\,; \enspace x_{2} \approx 3{,}46\]
Nachweis der Art der Extremstellen:
Es bietet sich der Nachweis der Art der Extremstellen mithilfe der zweiten Ableitung an (vgl. Abiturskript - 1.5.3 Monotonieverhalten, Extrem- und Terrassenpunkte).
Die zweite Ableitung \(A''\) der Funktion \(A\) kann wiederum mithilfe der Faktorregel, der Summenregel und der Potenzregel formuliert werden (vgl. Abiturskript - 1.5.2 Ableitungsregeln).
\[A'(x) = -0{,}72x^{2} + 3{,}36x - 3\]
\[\begin{align*}A''(x) &= -0{,}72 \cdot 2x + 3{,}36 \\[0.8em] &= -1{,}44x + 3{,}36 \end{align*}\]
Wert der zweiten Ableitung \(A''\) an den relativen Extremstellen \(x_{1} = 1{,}20\) und \(x_{2} = 3{,}46\) berechnen:
\[A''(1{,}20) = -1{,}44 \cdot 1{,}20 + 3{,}36 = 1{,}632\]
\[\left. \begin{align*} &A'(1{,}20) = 0 \\[0.8em] &A''(1{,}20) < 0 \end{align*} \right\} \enspace \Rightarrow \enspace \text{relatives Minimum}\]
\[A''(3{,}46) = -1{,}44 \cdot 3{,}46 + 3{,}36 = -1{,}6224\]
\[\left. \begin{align*} &A'(3{,}46) = 0 \\[0.8em] &A''(3{,}46) > 0 \end{align*} \right\} \enspace \Rightarrow \enspace \text{relatives Maximum}\]
\[\begin{align*}A(1{,}20) &= -0{,}24 \cdot 1{,}20^{3} + 1{,}68 \cdot 1{,}20^{2} - 3 \cdot 1{,}20 + 21 \\[0.8em] &\approx 19{,}40 \end{align*}\]
\[\begin{align*}A(3{,}46) &= -0{,}24 \cdot 3{,}46^{3} + 1{,}68 \cdot 3{,}46^{2} - 3 \cdot 3{,}46 + 21 \\[0.8em] &\approx 20{,}79 \end{align*}\]
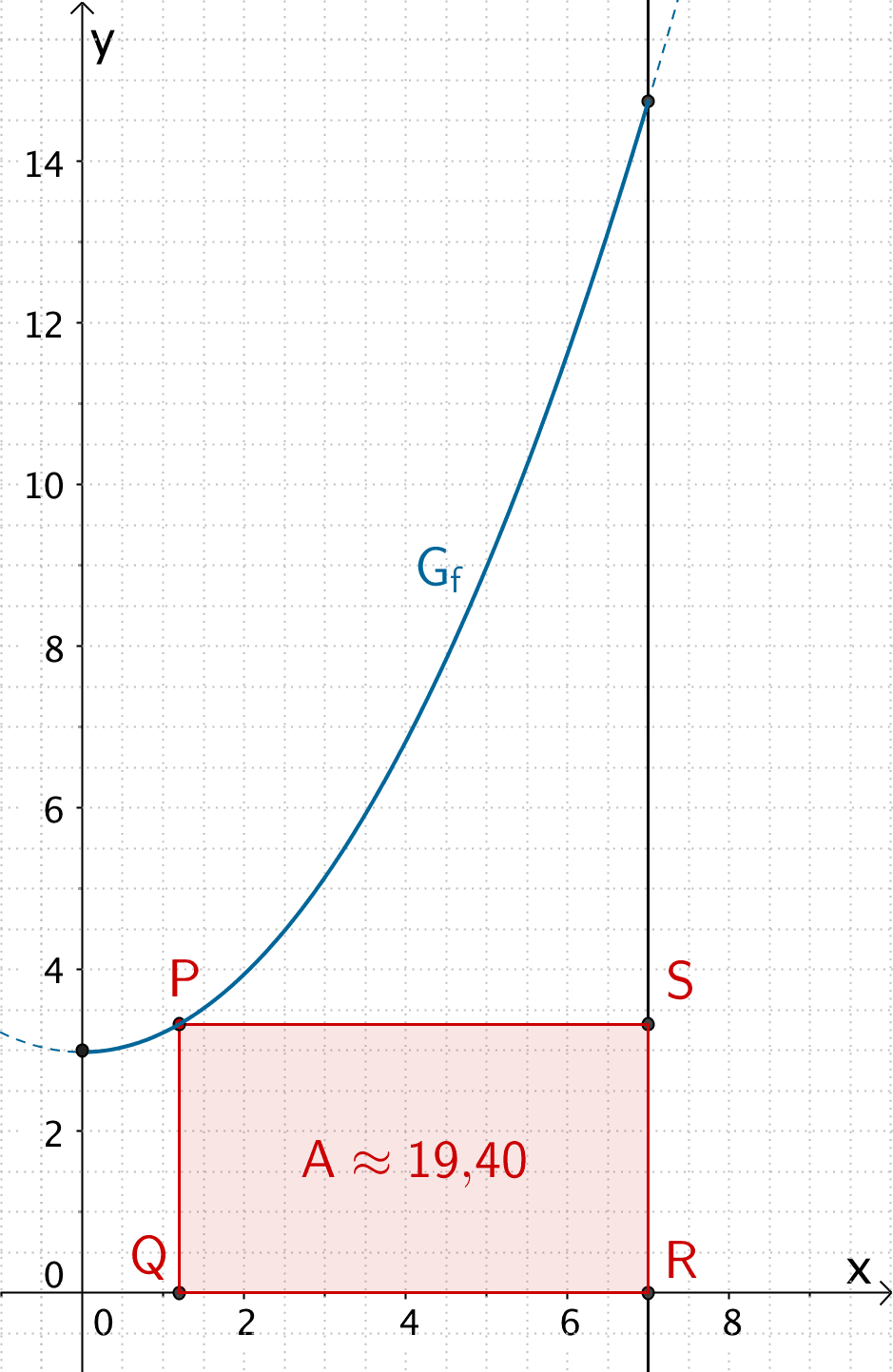
Relatives Minimum des Flächeninhalts \(A\) des Rechtecks \(QRSP\)
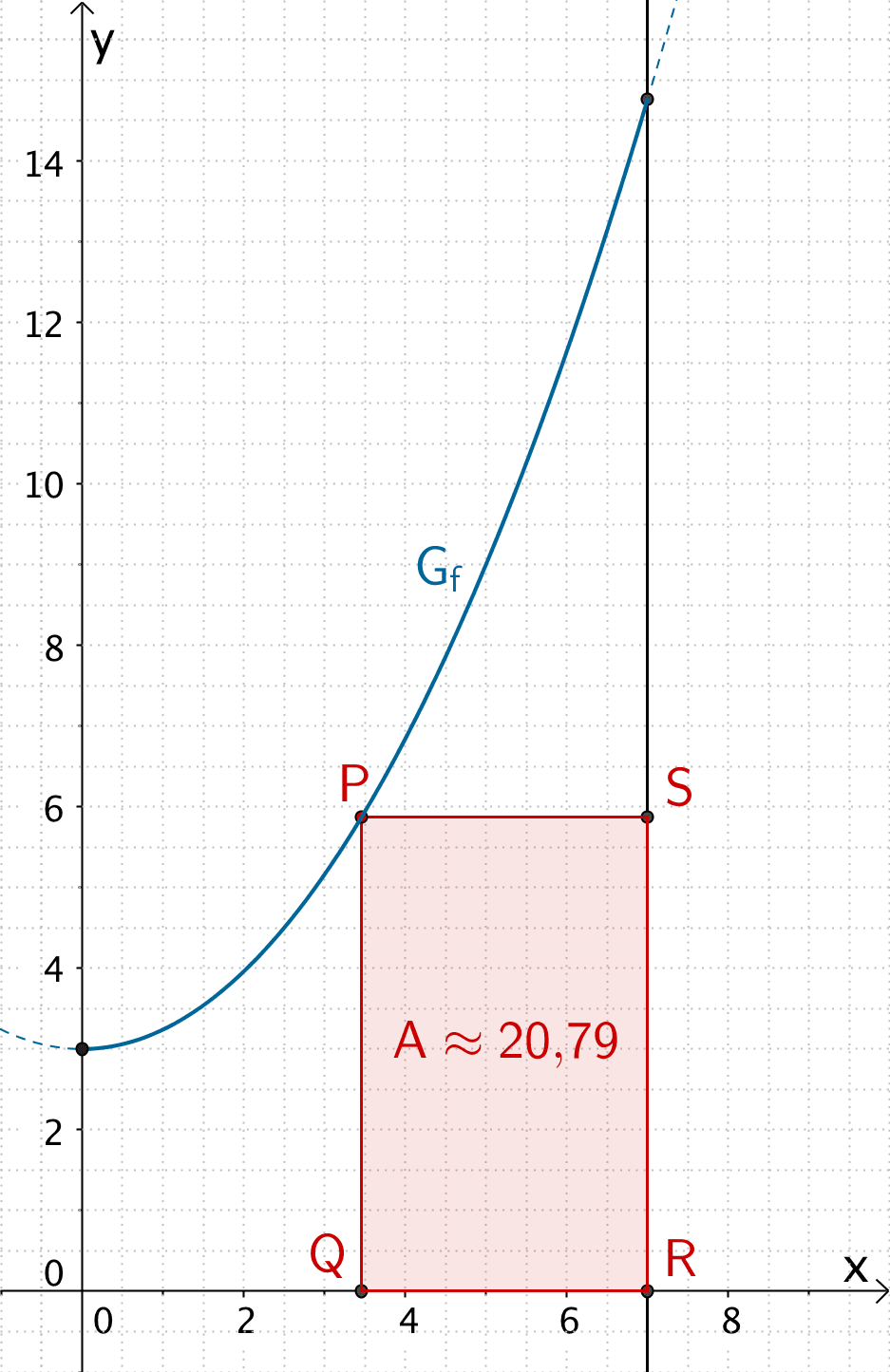
Relatives Maximum des Flächeninhalts \(A\) des Rechtecks \(QRSP\)
Das relative Minimum des Flächeninhalts ist nur von theoretischem Wert. Denn der Flächeninhalt \(A(x) = \overline{QR}(x) \cdot \overline{QP}(x)\) wird für \(x \to 7\) (\(x\)-Koordinate des Punktes \(P\)) beliebig klein, weil die Länge der Strecke \(\overline{QR}(x) = 7 - x\) beliebig klein wird. Somit existiert kein endlicher minimaler Flächeninhalt der Rechtecke \(QRSP\).
3. Relatives Maximum mit dem möglichem Randmaximum vergleichen:
Das relative Maximum des Flächeninhalts \(A\) muss mit dem Wert \(A(0)\) verglichen werden, da für \(x = 0\) ein Rechteck \(QRSP\) existiert.
Relatives Maximum: \(A(3{,}46) = 20{,}79\)
Randwert: \(A(0) = -0{,}24 \cdot 0^{3} + 1{,}68 \cdot 0^{2} - 3 \cdot 0 + 21 = 21\)
\(\Longrightarrow \quad\)Für \(x = 0\) liegt ein Randmaximum mit dem Flächeninhalt \(A = 21\) FE (Flächeneinheiten) vor.
Koordinaten des Punktes \(P\), sodass der Flächeninhalt \(A\) maximal ist:
\[f(x) = 0{,}24x^{2}+3\]
\[f(0) = 0{,}24 \cdot 0^{2}+3 = 3\]
\[\Longrightarrow \quad P(0|3)\]
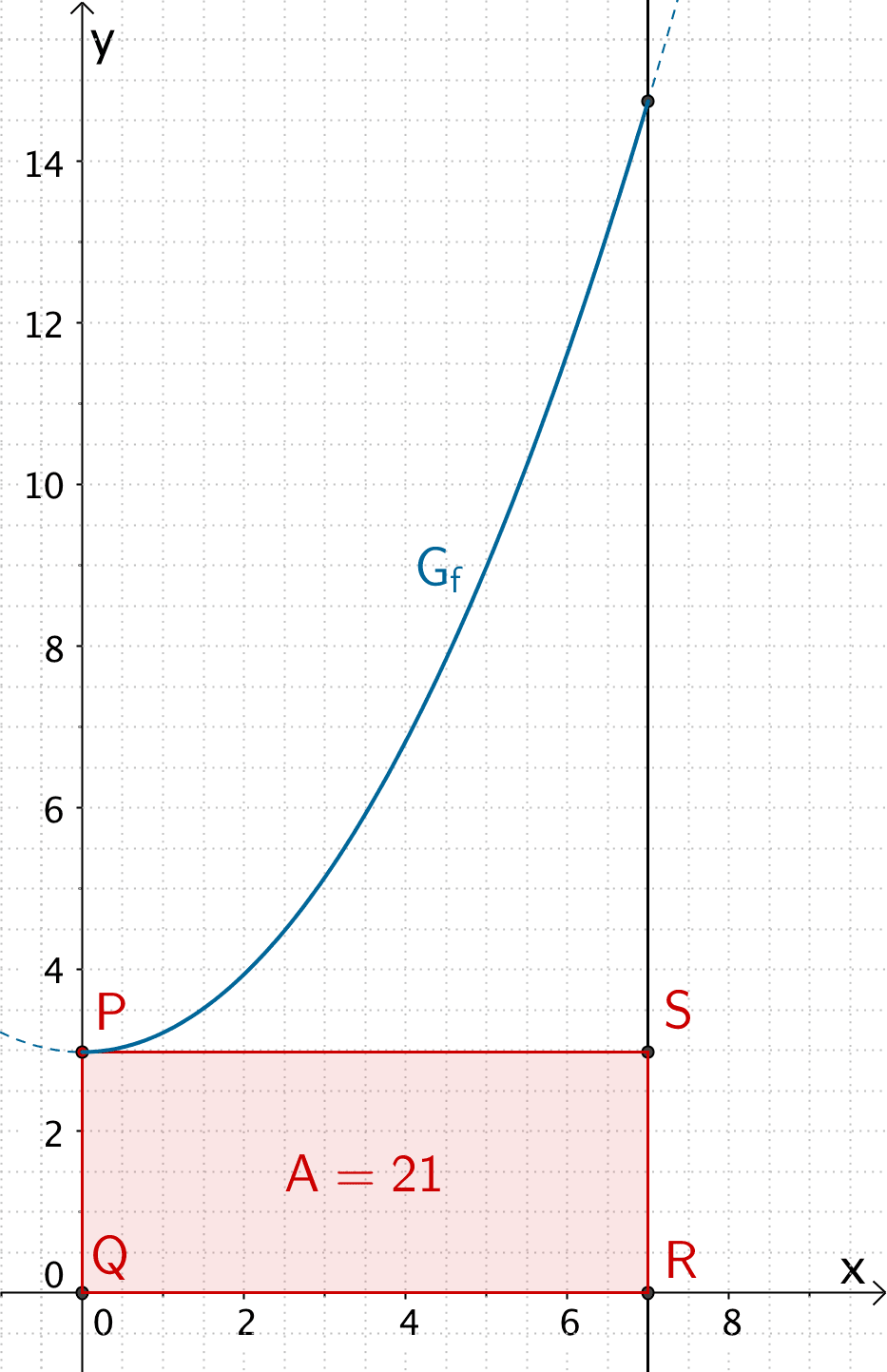
Randmaximum des Flächeninhalts \(A\) der Rechtecke \(QRSP\) mit \(A = 21\) FE (Flächeneinheiten) für \(P(0|3)\)
Wie das Beispiel zeigt, ist es bei Extremwertaufgaben besonders wichtig, die Ränder des Definitionsbereichs der Zielfunktion in die Extremwertbetrachtung mit einzubeziehen.
Beispielaufgabe
Einer Kugel mit dem Radius \(R = 10\) cm soll ein gerader Kreiszylinder zentrisch zur Mittelpunktsachse der Kugel so einbeschrieben werden, dass das Volumen des Zylinders maximal ist (vgl. Abbildung).
Bestimmen Sie das maximale Volumen \(V_{\text{max}}\) des Zylinders. Auf das Mitführen von Einheiten kann verzichtet werden.
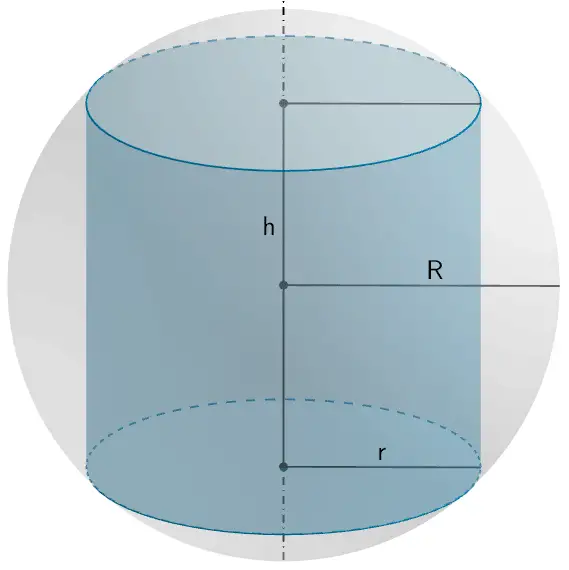
1. Zielfunktion formulieren:
Die Zielfunktion beschreibt das Volumen des Zylinders, welches zunächst in Abhängigkeit vom Radius \(r\) und von der Höhe \(h\) des Zylinders allgemein angegeben werden kann (vgl. Merkhilfe).
\[V = r^{2}\cdot \pi \cdot h\]
Um im zweiten Schritt mithilfe der Differentialrechnung das maximale Volumen bestimmen zu können, muss der Funktionsterm für das Zylindervolumen in Abhängigkeit von nur einer Variablen formuliert werden. Da sich der Radius \(r\) des einbeschriebenen Zylinders mit der Höhe \(h\) des Zylinder ändert und umgekehrt, ist es grundsätzlich möglich, den Funktionsterm entweder in Abhängigkeit des Radius \(r\) oder in Abhängigkeit der Höhe \(h\) zu beschreiben. In beiden Fällen ist eine Nebenbedingung erforderlich, welche einen mathematischen Zusammenhang zwischen dem Radius \(r\) und der Höhe \(h\) des Zylinders liefert.
Nebenbedingung formulieren:
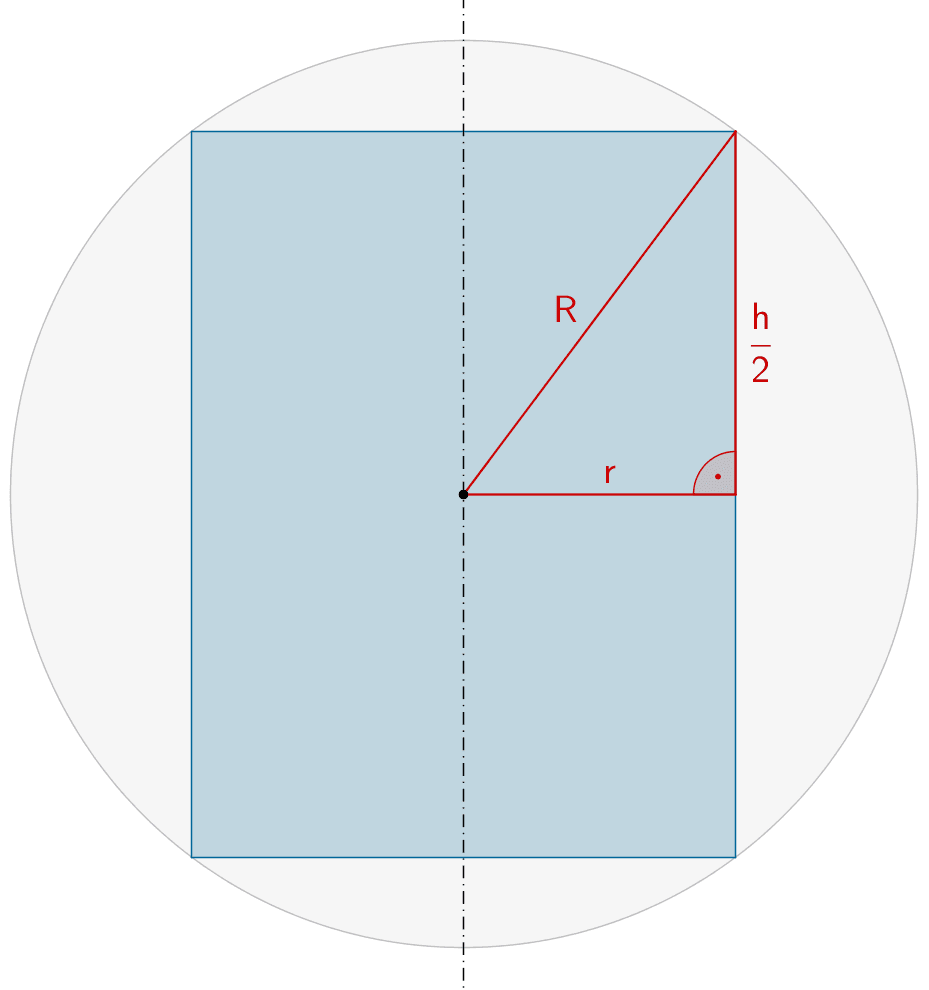
Mithilfe des Satzes des Pythagoras lässt sich eine Beziehung zwischen dem Radius \(r\) und der Höhe \(h\) des Zylinders formulieren. Je nachdem, ob das Volumen des Zylinders in Abhängigkeit des Radius \(r\) oder der Höhe \(h\) formuliert werden soll, wird die Nebenbedingung entsprechend aufgelöst.
Satz des Pythagoras anwenden:
\[\begin{align*}r^{2} + \left(\frac{h}{2}\right)^{2} &= R^{2} \\[0.8em] r^{2} + \frac{h^{2}}{4} &= R^{2} & &| - \frac{h^{2}}{4} \\[0.8em] r^{2} &= R^{2} - \frac{h^{2}}{4} \\[0.8em] r^{2} &= 10^{2} - \frac{h^{2}}{4} \\[0.8em] r^{2} &= 100 - \frac{h^{2}}{4} & &| \; \sqrt{\enspace}, \; r > 0 \\[0.8em] r &= \sqrt{100 - \frac{h^{2}}{4}}\end{align*}\]
\[\begin{align*} r^{2} + \left(\frac{h}{2}\right)^{2} &= R^{2} \\[0.8em] r^{2} + \frac{h^{2}}{4} &= R^{2} & &| - r^{2} \\[0.8em] \frac{h^{2}}{4} &= R^{2} - r^{2} & &| \cdot 4 \\[0.8em] h^{2} &= 4 \cdot (R^{2} - r^{2}) & &| \; \sqrt{\enspace}, \; h > 0 \\[0.8em] h &= \sqrt{4 \cdot (R^{2} - r^{2})} \\[0.8em] h &= 2\sqrt{R^{2} - r^{2}} \\[0.8em] h &= 2\sqrt{10^{2} - r^{2}} \\[0.8em] h &= 2\sqrt{100 - r^{2}}\end{align*}\]
Mit \(V = r^{2}\cdot \pi \cdot h\) ergibt sich:
\[\begin{align*}V(h) &= \left( 100 - \frac{h^{2}}{4} \right) \cdot \pi \cdot h \\[0.8em] &= -\frac{\pi}{4}h^{3} + 100\pi h \end{align*}\]
\[\begin{align*}V(r) &= r^{2} \cdot \pi \cdot 2\sqrt{100 - r^{2}} \\[0.8em] &= 2 \pi r^{2} \cdot \sqrt{100 - r^{2}} \end{align*}\]
Sinnvoller Definitionsbereich für \(V(h)\) bzw. \(V(r)\):
Die Zielfunktion \(V(h)\) bzw. \(V(r)\) beschreibt das Volumen eines einer Kugel einbeschriebenen Zylinders. Der Radius \(R = 10\) cm beschränkt die Höhe \(h\) und den Radius \(r\) des Zylinders. Für \(h \to 0\) bzw. \(r \to 0\) sowie für \(h \to 2R\) bzw. \(r \to R\) existiert jeweils kein Zylinder mehr.
\[\Longrightarrow \quad V(h) = -\frac{\pi}{4}h^{3} + 100\pi h\,; \enspace D_{V} = ]0;20[\]
bzw.
\[\Longrightarrow \quad V(r) = 2 \pi r^{2} \cdot \sqrt{100 - r^{2}}; \enspace D_{V} = ]0;10[\]
2. Zielfunktion \(V(h)\) oder \(V(r)\) auf relative Extremstellen hin untersuchen:
Die Aufgabenstellung fragt nach dem maximalen Volumen des Zylinders. Zudem ist offensichtlich, dass das Zylindervolumen an den Definitionsrändern beliebig klein wird. Ein Nachweis der Art der Extremstelle kann deshalb entfallen.
Notwendige Bedingung für eine Extremstelle von \(V(h)\) bzw. \(V(r)\):
\(V'(h) \overset{!}{=} 0\) bzw. \(V'(r) \overset{!}{=} 0\)
Erste Ableitung \(V'(h)\) oder \(V'(r)\) bilden:
Die erste Ableitung V'(h) bzw. \(V'(r)\) kann mithilfe der Faktor-, Summen-, Potenz-, Produkt-, und Kettenregel formuliert werden (vgl. Abiturskript - 1.5.2 Ableitungsregeln).
Zielfunktion \(V(h)\) auf relative Extremstellen hin untersuchen:
\[V(h) = -\frac{\pi}{4}h^{3} + 100\pi h\]
\[\begin{align*} V'(h) &= \left(-\frac{\pi}{4}\right) \cdot 3h^{2} + 100 \pi \\[0.8em] &= -\frac{3}{4}\pi h^{2} + 100\pi \end{align*}\]
\[\begin{align*} -\frac{3}{4} \pi h^{2} + 100\pi &= 0 & &| - 100\pi \\[0.8em] -\frac{3}{4} \pi h^{2} &= - 100\pi & &| : \left( -\frac{3}{4}\pi \right) \\[0.8em] h^{2} &= \frac{-100 \cancel{\pi}}{-\frac{3}{4} \cancel{\pi}} \\[0.8em] h^{2} &= 100 \cdot \frac{4}{3} \\[0.8em] h^{2} &= \frac{400}{3} & &| \; \sqrt{\enspace}, \; h > 0 \\[0.8em] h &= \frac{20}{\sqrt{3}} \\[0.8em] &= \frac{20}{3}\sqrt{3} \end{align*}\]
Mit \(r = \sqrt{100 - \frac{h^{2}}{4}}\) folgt (siehe Nebenbedingung):
\[\begin{align*} r &= \sqrt{100 - \frac{\left( \frac{20}{3}\sqrt{3} \right)^{2}}{4}} \\[0.8em] &= \sqrt{100 - \frac{\frac{400}{9} \cdot 3}{4}} \\[0.8em] &= \sqrt{100 - \frac{100}{3}} \\[0.8em] &= \sqrt{\frac{300}{3} - \frac{100}{3}} \\[0.8em] &= \sqrt{\frac{200}{3}} \\[0.8em] &= \sqrt{100 \cdot \frac{2}{3}} \\[0.8em] &= \sqrt{100 \cdot \frac{6}{9}} \\[0.8em] &= \frac{10}{3}\sqrt{6} \end{align*}\]
Für \(h = \frac{20}{3}\sqrt{3}\) cm und \(r = \frac{10}{3}\sqrt{6}\) cm ist das Volumen des der Kugel einbeschriebenen Zylinders für \(h \in \;]0;20[\) bzw. \(r \in \; ]0;10[\) maximal.
oder
Zielfunktion \(V(r)\) auf relative Extremstellen hin untersuchen:
\[V(r) = 2 \pi r^{2} \cdot \sqrt{100 - r^{2}} = 2\pi r^{2} \cdot \left( 100 - r^{2} \right)^{\frac{1}{2}}\]
\[\begin{align*}V'(r) &= 2 \cdot 2\pi r \cdot \sqrt{100 - r^{2}} + \cancel{2}\pi r^{2} \cdot \frac{1}{\cancel{2}} \cdot \left( 100 - r^{2} \right)^{-\frac{1}{2}} \cdot (-2r) \\[0.8em] &= 4 \pi r \sqrt{100 - r^{2}} - \frac{2 \pi r^{3}}{\sqrt{100 - r^{2}}} \\[0.8em] &= \frac{4 \pi r \sqrt{100 - r^{2}} \cdot \sqrt{100 - r^{2}} - 2 \pi r^{3}}{\sqrt{100 - r^{2}}} \\[0.8em] &= \frac{4 \pi r (100 - r^{2}) - 2 \pi r^{3}}{\sqrt{100 - r^{2}}} \\[0.8em] &= \frac{400 \pi r - 4 \pi r^{3} - 2 \pi r^{3}}{\sqrt{100 - r^{2}}} \\[0.8em] &= \frac{-6 \pi r^{3} + 400 \pi r}{\sqrt{100 - r^{2}}} \end{align*}\]
\[\begin{align*} \Longrightarrow \quad -6 \pi r^{3} + 400 \pi r &= 0 \\[0.8em] r \cdot (-6 \pi r^{2} + 400 \pi) &= 0 & &| \; r \neq 0 \end{align*}\]
\[\begin{align*} \Longrightarrow \quad -6 \pi r^{2} + 400 \pi &= 0 & &| - 400 \pi \\[0.8em] -6 \pi r^{2} &= -400 \pi & &| : (-6 \pi) \\[0.8em] r^{2} &= \frac{-400 \cancel{\pi}}{-6 \cancel{\pi}} \\[0.8em] r^{2} &= \frac{200}{3} & &| \; \sqrt{\enspace}, \; r > 0 \\[0.8em] r &= \sqrt{\frac{200}{3}} \\[0.8em] &= \sqrt{100 \cdot \frac{2}{3}} \\[0.8em] &= \sqrt{100 \cdot \frac{6}{9}} \\[0.8em] &= \frac{10}{3}\sqrt{6} \end{align*}\]
Mit \(h = 2\sqrt{100 - r^{2}}\) folgt (siehe Nebenbedingung):
\[\begin{align*} h &= 2 \sqrt{100 - \left( \frac{10}{3}\sqrt{6} \right)^{2}} \\[0.8em] &= 2 \sqrt{100 - \frac{100}{9} \cdot 6} \\[0.8em] &= 2 \sqrt{100 - \frac{100}{3} \cdot 2} \\[0.8em] &= 2 \sqrt{100 - \frac{200}{3}} \\[0.8em] &= 2 \sqrt{\frac{300}{3} - \frac{200}{3}} \\[0.8em] &= 2 \sqrt{\frac{100}{3}} \\[0.8em] &= \frac{20}{\sqrt{3}} \\[0.8em] &= \frac{20}{3}\sqrt{3} \end{align*}\]
Für \(r = \frac{10}{3}\sqrt{6}\) cm und \(h = \frac{20}{3}\sqrt{3}\) cm ist das Volumen des der Kugel einbeschriebenen Zylinders für \(r \in \; ]0;10[\) bzw. \(h \in \; ]0;20[\) maximal.
Relatives maximales Volumen \(V_{\text{max}}\) des Zylinders berechnen:
\[V = r^{2} \cdot \pi \cdot h\]
\[\begin{align*}V_{\text{max}} &= \left( \frac{10}{3}\sqrt{6} \right)^{2} \cdot \pi \cdot \frac{20}{3} \sqrt{3} \\[0.8em] &= \frac{100}{9} \cdot 6 \cdot \pi \cdot \frac{20}{3}\sqrt{3} \\[0.8em] &= \frac{200}{3}\pi \cdot \frac{20}{3}\sqrt{3} \\[0.8em] &= \frac{4000}{9}\sqrt{3} \pi \\[0.8em] &\approx 2418{,}40 \end{align*}\]
oder
\[V(h) = -\frac{\pi}{4}h^{3} + 100 \pi h\]
\[\begin{align*} V_{\text{max}} &= V\left( \frac{20}{3}\sqrt{3} \right) \\[0.8em] &= -\frac{\pi}{4} \cdot \left( \frac{20}{3}\sqrt{3} \right)^{3} + 100 \pi \cdot \frac{20}{3} \sqrt{3} \\[0.8em] &= -\frac{\pi}{4} \cdot \frac{8000}{27} \cdot 3\sqrt{3} + \frac{2000}{3}\sqrt{3} \pi \\[0.8em] &= -\frac{2000}{9}\sqrt{3} \pi + \frac{6000}{9} \sqrt{3} \pi \\[0.8em] &= \frac{4000}{9}\sqrt{3} \pi \\[0.8em] &\approx 2418{,}40 \end{align*}\]
oder
\[V(r) = 2 \pi r^{2} \cdot \sqrt{100 - r^{2}}\]
\[\begin{align*} V_{\text{max}} &= V\left( \frac{10}{3}\sqrt{6} \right) \\[0.8em] &= 2 \pi \cdot \left( \frac{10}{3}\sqrt{6} \right)^{2} \cdot \sqrt{100 - \left( \frac{10}{3}\sqrt{6} \right)^{2}} \\[0.8em] &= 2 \pi \cdot \frac{100}{9} \cdot 6 \cdot \sqrt{100 - \frac{100}{9} \cdot 6} \\[0.8em] &= \frac{400}{3}\pi \cdot \sqrt{100 - \frac{200}{3}} \\[0.8em] &= \frac{400}{3} \pi \cdot \sqrt{\frac{300}{3} - \frac{200}{3}} \\[0.8em] &= \frac{400}{3} \pi \cdot \sqrt{\frac{100}{3}} \\[0.8em] &= \frac{400}{3} \pi \cdot \frac{10}{\sqrt{3}} \\[0.8em] &= \frac{400}{3} \pi \cdot \frac{10 \sqrt{3}}{3} \\[0.8em] &= \frac{4000}{9}\sqrt{3} \pi \\[0.8em] &\approx 2418{,}40 \end{align*}\]
3. Relatives maximales Volumen mit möglichen Randmaxima vergleichen:
\(V_{\text{max}} \approx 2418{,}40\)
\[V(h) = -\frac{\pi}{4}h^{3} + 100\pi h\,; \enspace D_{V} = ]0;20[\]
\[V(r) = 2 \pi r^{2} \cdot \sqrt{100 - r^{2}}; \enspace D_{V} = ]0;10[\]
Bei der Wahl eines sinnvollen Definitionsbereichs der Zielfunktionen \(V(h)\) bzw. \(V(r)\) wurden die offenen Intervalle \(h \in \: ]0;20[\) bzw. \(r \in \: ]0;10[\) festgelegt. Das heißt, die Zielfunktionen sind für \(h = 0\) und \(h = 20\) sowie für \(r = 0\) und \(r = 10\) nicht definiert. Folglich kann es keine Randmaxima geben.
Der maximales Volumeninhalt des der Kugel einbeschriebenen Zylinders beträgt 2418,40 cm³.
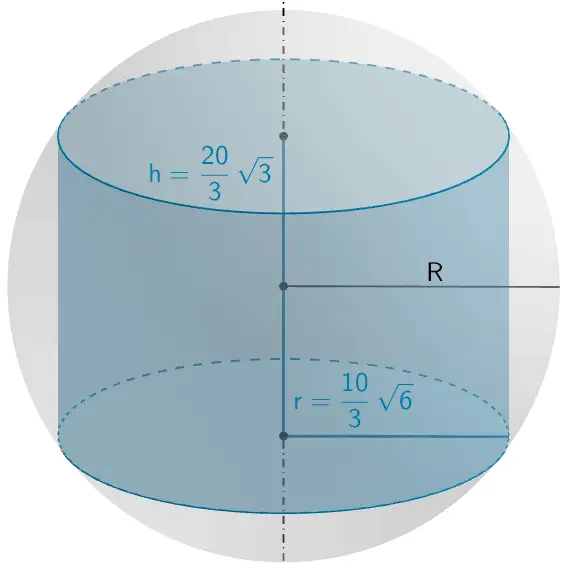
Einbeschriebener Zylinder mit maximalem Volumen

