Das bestimmte Integral \(\displaystyle \int_{a}^{b} f(x)\, dx\) errechnet die Maßzahl der Flächenbilanz des Flächeninhalts, den der Graph der Funktion \(f\) im Intervall \([a;b]\) mit der \(x\)-Achse einschließt. Dabei werden für \(a < b\) Flächeninhalte von Flächenstücken unterhalb der \(x\)-Achse negativ gezählt und Flächeninhalte von Flächenstücken oberhalb der \(x\)-Achse positiv gezählt.
Bestimmtes Integral (vgl. Merkhilfe)
\(\displaystyle \int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\), wobei \(F\) eine Stammfunktion von \(f\) ist.
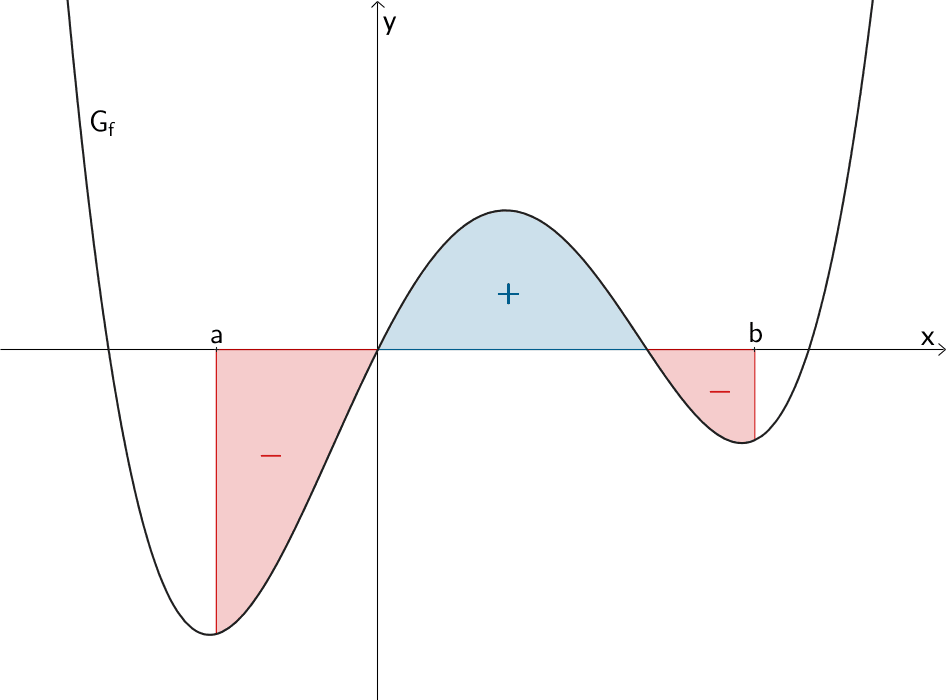
Flächenbilanz für \(a < b\): Flächeninhalte von Flächenstücken unterhalb der \(x\)-Achse zählen negativ und Flächeninhalte von Flächenstücken oberhalb der \(x\)-Achse zählen positiv.
Bestimmtes Integral im Sachzusammenhang
Beschreibt eine Funktion \(f\) die momentane Änderungsrate einer Größe in Abhängigkeit von der Zeit \(t\), so errechnet das bestimmte Integral \(\displaystyle \int_{t_{1}}^{t_{2}} f(t)\,dt\) den Wert der Gesamtänderung der Größe im Zeitintervall \([t_{1};t_{2}]\).
Beispiel:
Die Funktion \(f\) beschreibt den Wasserdurchfluss an einer bestimmten Messstelle eines Wasserroheres in Kubikmetern pro Minute. Dann errechnet das bestimmte Integral \(\displaystyle \int_{2}^{5} f(t)\,dt\) die Wassermenge in Kubikmeter, welche im Zeitintervall \(t \in [2;5]\) (\(t\) in Minuten) an der Messstelle durch das Wasserrohr fließt.
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
Beispielaufgabe
Gegeben sei die in \(\mathbb R_{0}^{+}\) definierte Funktion \(f \colon x \mapsto 2\sqrt{x} \cdot(1 - 0{,}5x)\).
Berechnen Sie den Wert des Integrals \(\displaystyle \int_{4}^{0} 2\sqrt{x} \cdot (1 - 0{,}5x) \, dx\) und deuten Sie das Ergebnis geometrisch.
Wert des Integrals \(\displaystyle \int_{4}^{0} 2\sqrt{x} \cdot (1 - 0{,}5x) \, dx\)
Stammfunktion \(F\) der Funktion \(f\):
Um eine Stammfunktion \(F\) der Funktion \(f\) bestimmen zu können, wird der Funktionsterm \(f(x)\) zunächst in eine Summe von Potenzen umgeformt.
\[\begin{align*} f(x) &=2\sqrt{x} \cdot (1 - 0{,}5x) \\[0.8em] &= 2\sqrt{x} - \sqrt{x}x & &| \; \sqrt{x} = x^{\frac{1}{2}} \\[0.8em] &= 2 \cdot x^{\frac{1}{2}} - x^{\frac{1}{2}} \cdot x & &| \; a^{m} \cdot a^{n} = a^{m + n} \\[0.8em] &= 2 \cdot x^{\frac{1}{2}} - x^{\frac{3}{2}} \end{align*}\]
Mithilfe des unbestimmten Integrals \(\displaystyle \int x^{r} dx = \frac{x^{r + 1}}{r + 1} + C\) lässt sich der Funktionsterm \(F(x)\) der Menge aller Stammfunktionen von \(f\) beschreiben (vgl. Abiturskript - 1.6.2 Unbestimmtes Integral/Wichtige unbestimmte Integrale).
\[\begin{align*} F(x) &= 2 \cdot \frac{1}{\frac{1}{2} + 1} \cdot x^{\frac{1}{2} + 1} - \frac{1}{\frac{3}{2} + 1} \cdot x^{\frac{3}{2} + 1} + C \\[0.8em] &= 2 \cdot \frac{1}{\frac{3}{2}} \cdot x^{\frac{3}{2}} - \frac{1}{\frac{5}{2}} \cdot x^{\frac{5}{2}} + C \\[0.8em] &= \frac{4}{3} \cdot x^{\frac{3}{2}} - \frac{2}{5} \cdot x^{\frac{5}{2}} + C \\[0.8em] &= 2x^{\frac{3}{2}} \cdot \left( \frac{2}{3} - \frac{1}{5}x \right) + C \\[0.8em] &= 2\sqrt{x^{3}} \cdot \left( \frac{2}{3} - \frac{1}{5}x \right) + C\end{align*}\]
\(\displaystyle \Longrightarrow \quad F_{0}(x) = 2\sqrt{x^{3}} \cdot \left( \frac{2}{3} - \frac{1}{5}x \right)\) ist einen Stammfunktion von \(f\) (für \(C = 0\)).
Wert des Integrals \(\displaystyle \int_{4}^{0} 2\sqrt{x} \cdot (1 - 0{,}5x) \, dx\) berechnen:
\[\begin{align*} \int_{4}^{0} 2\sqrt{x} \cdot (1 - 0{,}5x) \, dx &= \left[ 2\sqrt{x^{3}} \cdot \left( \frac{2}{3} - \frac{1}{5}x \right) \right]_{4}^{0} \\[0.8em] &= 2\sqrt{0^{3}} \cdot \left( \frac{2}{3} - \frac{1}{5} \cdot 0 \right) - \left[ 2\sqrt{4^{3}} \cdot \left( \frac{2}{3} - \frac{1}{5} \cdot 4 \right) \right] \\[0.8em] &= 0 - 16 \cdot \left( \frac{2}{3} - \frac{4}{5} \right) \\[0.8em] &= (-16) \cdot \left( \frac{10}{15} - \frac{12}{15} \right) \\[0.8em] &= (-16) \cdot \left( -\frac{2}{15} \right) \\[0.8em] &= \frac{32}{15} \\[0.8em] &\approx 2{,}13 \end{align*}\]
Geometrische Bedeutung des Ergebnisses
Das Ergebnis \(\displaystyle \int_{4}^{0} 2\sqrt{x} \cdot (1 - 0{,}5x) \, dx \approx 2{,}13\) drückt eine positive Flächenbilanz aus.
Da die obere Integrationsgrenze kleiner ist als die untere Integrationsgrenze, bedeutet die positive Flächenbilanz in diesem Fall, dass die Fläche, die der Graph der Funktion \(f\) im Intervall \([0;4]\) mit der \(x\)-Achse einschließt, überwiegend unterhalb der \(x\)-Achse liegen muss.
Denn mit \(\displaystyle \int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\) gilt:
\[\int_{0}^{4} 2\sqrt{x} \cdot (1 - 0{,}5x) \, dx \approx -2{,}13\]
Für eine genauere Aussage betrachtet man die Nullstelle(n) der Funktion \(f\).
\[f(x) = 2\sqrt{x} \cdot(1 - 0{,}5x); \; D_{f} = \mathbb R_{0}^{+}\]
\[2\sqrt{x} \cdot (1 - 0{,}5x) = 0\]
\[\begin{align*}x = 0 \enspace \vee \enspace 1 -0{,}5x &= 0 & &| + 0{,}5x \\[0.8em] 1 &= 0{,}5x & &| \cdot 2 \\[0.8em] 2 &= x \end{align*}\]
Die Nullstelle \(x = 0\) ist zugleich Definitions- und Integrationsgrenze und spielt bei der Betrachtung der Flächenbilanz keine Rolle.
An der einfachen Nullstelle \(x = 2\) wechselt die Funktion \(f\) das Vorzeichen von \(+\) nach \(-\). Folglich verläuft der Graph der Funktion \(f\) im Intervall \([0;2[\) oberhalb der \(x\)-Achse und im Intervall \(]2;4]\) unterhalb der \(x\).Achse.
Da mit \(\displaystyle \int_{4}^{0} 2\sqrt{x} \cdot (1 - 0{,}5x) \, dx\) „nach links" integriert wird (obere Integrationsgrenze kleiner als unter Integrationsgrenze), zählt das Integral den Flächeninhalt des im Intervall \([0;2]\) oberhalb der \(x\)-Achse liegenden Flächenstücks negativ und den Flächeninhalt des im Intervall \([2;4]\) unterhalb der \(x\)-Achse liegenden Flächenstücks positiv.
Schlussfolgerung:
\[\int_{4}^{0} f(x))\, dx = \underbrace{\int_{4}^{2} f(x)\, dx}_{>\, 0} + \underbrace{\int_{2}^{0} f(x)\, dx}_{< \, 0} \approx 2{,}13\]
Der Flächeninhalt des Flächenstücks, das \(G_{f}\) im Intervall \([2;4]\) mit der \(x\)-Achse einschließt ist größer als der Flächeninhalt des Flächenstücks, das \(G_{f}\) im Intervall \([0;2]\) mit der \(x\)-Achse einschließt.
![Flächenstücke, die der Graph der Funktion f im Intervall [0;4] mit der x-Achse einschließt Flächenstücke, die der Graph der Funktion f im Intervall [0;4] mit der x-Achse einschließt](/images/stories/abi_check/analysis/Int_Bestimmtes_Int_Bsp.png)
Flächenbilanz des Integrals \(\displaystyle \int_{4}^{0} 2\sqrt{x} \cdot(1 - 0{,}5x) = 2{,}13\), Flächenstücke, die \(G_{f}\) im Intervall \([0;4]\) mit der \(x\)- Achse einschließt.


