Eine Anwendung des bestimmten Integrals ist die Berechnung von Flächeninhalten. Zum einen lässt sich der Flächeninhalt, des Flächenstücks, das ein Funktionsgraph mit der \(x\)-Achse einschließt ermitteln, zum anderen kann der Flächeninhalt eines Flächenstücks, das zwei Funktionsgraphen einschließen, berechnet werden. Das Abschätzen solcher Flächeninhalte kann im umgekehrten Sinn dazu dienen, den Wert eines bestimmten Integrals näherungsweise zu bestimmen.
Abschätzen von Flächeninhalten - näherungsweise Integration
Um den Wert eines bestimmten Integrals \(\displaystyle \int_{a}^{b} f(x)\,dx\) näherungsweise zu bestimmen, kann der Flächeninhalt des Flächenstücks, das der Graph der Funktion \(f\) im Intervall \([a;b]\) mit der \(x\)-Achse einschließt abgeschätzt werden. Hierfür betrachtet man entweder geeignete Teilflächen oder bedient sich der Methode „Kästchen zählen".
Beispiel:
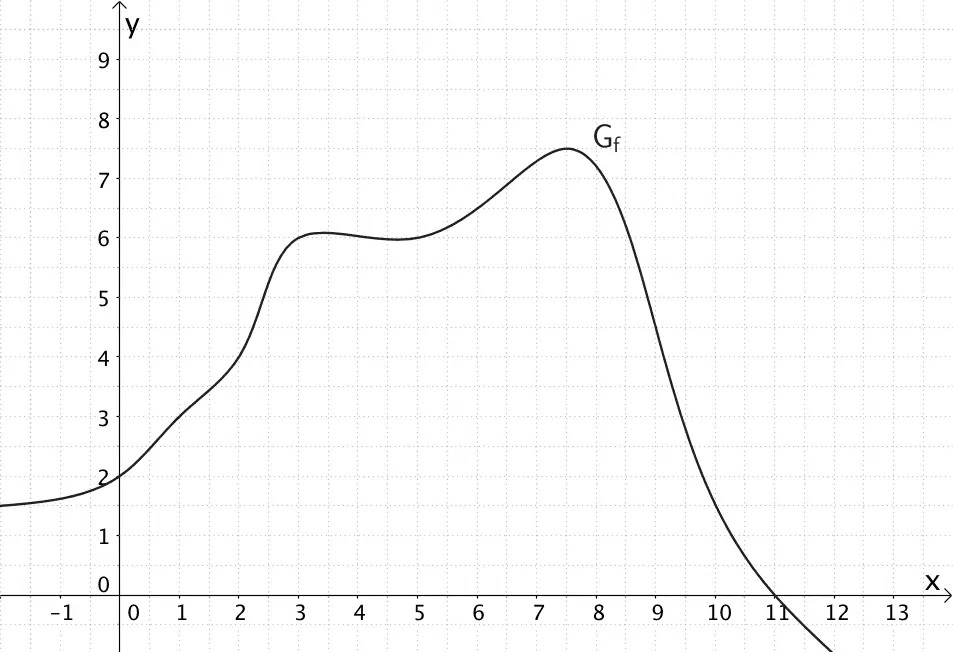
Die Abbildung zeigt den Graphen einer Funktion \(f\). Mithilfe der Abbildung soll näherungsweise der Wert des Integrals \(\displaystyle \int_{0}^{11} f(x)\, dx\) berechnet werden.
1. Möglichkeit: Zerlegung in geeignete Teilflächen
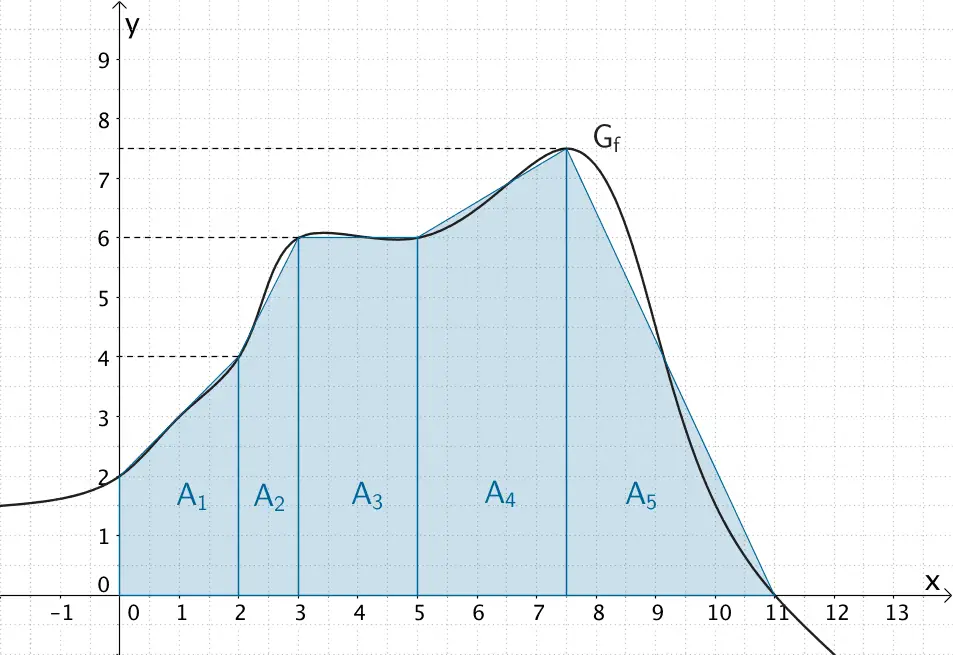
Das Flächenstück, welches \(G_{f}\) mit den Koordinatenachsen einschließt, lässt sich durch eine Zerlegung in Teilflächen (Trapez, Rechteck, Dreieck) annähern.
\[\begin{align*}\int_{0}^{11}f(x)\,dx &\approx A_{1} + A_{2} + A_{3} + A_{4} + A_{5} \\[0.8em] &= \frac{2 + 4}{2} \cdot 2 + \frac{4 + 6}{2} \cdot 1 + 2 \cdot 6 + \frac{6 + 7{,}5}{2} \cdot 2{,}5 + \frac{1}{2} \cdot 3{,}5 \cdot 7{,}5 \\[0.8em] &= 6 + 5 + 12 + \frac{135}{8} + \frac{105}{8} \\[0.8em] &= 53 \end{align*}\]
2. Möglichkeit: „Kästchen zählen"
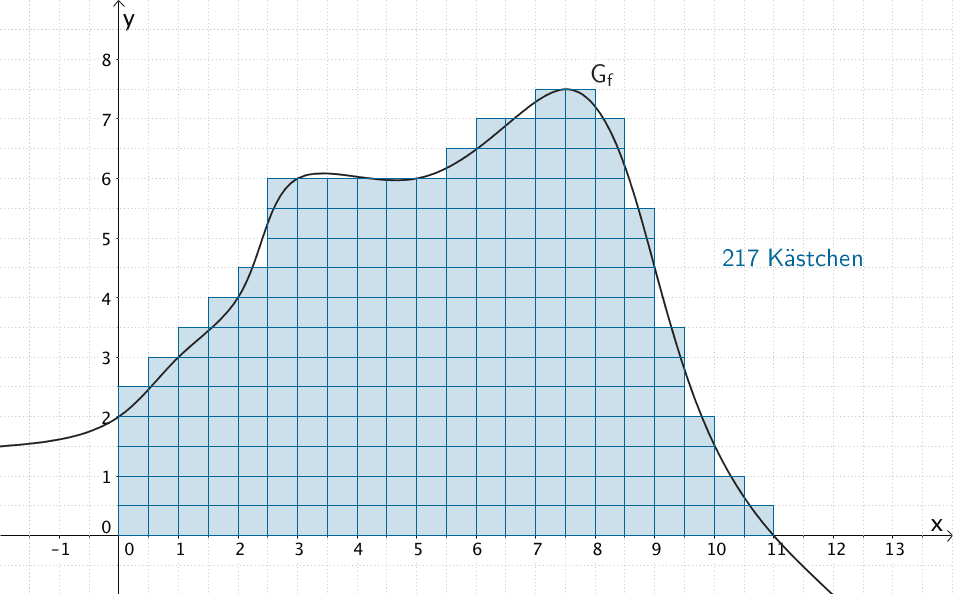
Annäherung des Flächenstücks, welches \(G_{f}\) mit den Koordinatenachsen einschließt durch 217 flächeninhaltsgleiche „Kästchen".
Flächeninhalt eines Kästchens: 0,25 FE (Flächeneinheiten)
\[\int_{0}^{11}f(x)\,dx \approx 217 \cdot 0{,}25 = 54{,}25\]
Flächeninhalt zwischen Funktionsgraph und \(x\)-Achse
Das bestimmte Integral \(\displaystyle \int_{a}^{b} f(x)\,dx\) berechnet die Maßzahl des Flächeninhalts \(A\) der Fläche, die der Graph einer Funktion \(f\) mit der \(x\)-Achse sowie den Geraden \(x = a\) und \(x = b\) einschließt. Voraussetzung hierfür ist, dass \(G_{f}\) im Intervall \([a;b]\) oberhalb der \(x\)-Achse verläuft (\(f(x) \geq 0\)) und dass „nach rechts" integriert wird (\(a < b\), obere Integrationsgrenze größer als untere Integrationsgrenze).
Liegt die Fläche, welche der Graph einer Funktion \(f\) im Intervall \([a;b]\) mit der \(x\)-Achse einschließt, teils oberhalb und teils unterhalb der \(x\)-Achse, müssen die Teilflächen getrennt betrachtet werden. Für die Berechnung der Flächeninhalte der Teilflächen werden die Nullstellen \(x_{1}, x_{2}, ... ,x_{n}\) der Funktion \(f\) im Intervall \([a;b]\) benötigt. Sie liefern die Integrationsgrenzen für die bestimmten Integrale der zu berechnenden Flächeninhalte der Teilflächen.
Liegt eine Teilfläche unterhalb der \(x\)-Achse, wählt man für das entsprechende bestimmte Integral entweder den Betrag oder ein negatives Vorzeichen, um einen positiven Wert zu berechnen.
Eine Untersuchung, welche der Teilflächen oberhalb bzw. unterhalb der \(x\)-Achse liegen, kann entfallen, wenn man für alle zu berechnende Teilflächen den Betrag des bestimmten Integrals wählt..
Der Flächeninhalt \(A\) der Fläche, die der Graph einer Funktion \(f\) im Intervall \([a;b]\) mit der \(x\)-Achse einschließt ist gleich der Summe der Flächeninhalte der Teilflächen \(A_{1}, A_{2}, ... ,A_{n}\).
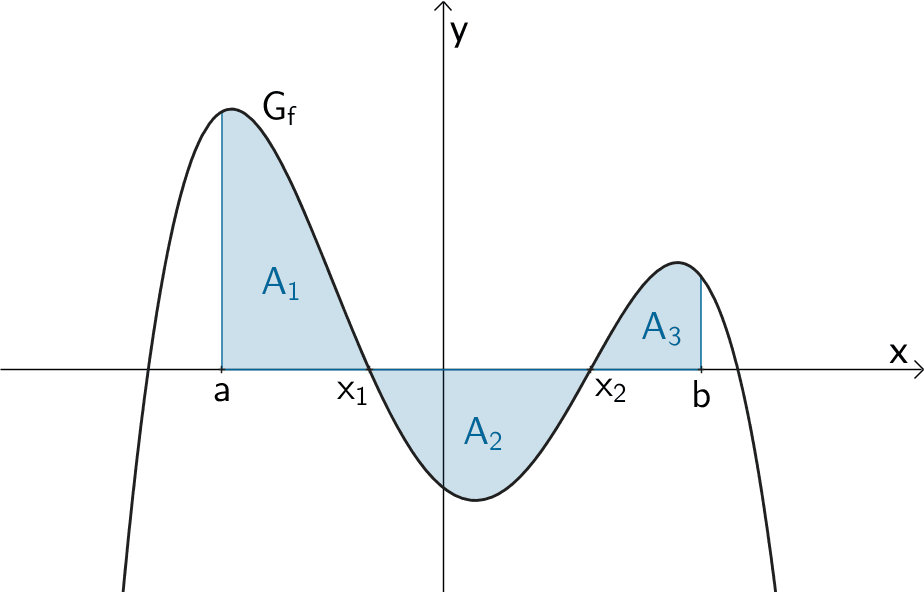
Beispiel: Flächeninhalte \(A_{1}\), \(A_{2}\) und \(A_{3}\), die \(G_{f}\) im Intervall \([a;b]\) mit der \(x\)-Achse einschließt.
\[\begin{align*} A &= A_{1} + A_{2} + ... + A_{n} \\[0.8em] &= \left| \int_{a}^{x_{1}} f(x) \,dx \, \right| + \left| \int_{x_{1}}^{x_{2}} f(x)\,dx\, \right| + ... + \left| \int_{x_{n}}^{b} f(x)\,dx\, \right| \end{align*}\]
Beispiel:
Berechnen Sie den Flächeninhalt \(A\) der Fläche, die der Graph der in \(\mathbb R\) definierten Funktion \(f \colon x \mapsto \frac{1}{4}x^{3} + \frac{1}{2}x^{2} - 2x\) für \(x \in [-3;3]\) mit der \(x\)-Achse einschließt.
\[f(x) = \frac{1}{4}x^{3} + \frac{1}{2}x^{2} - 2x\,; \enspace D_{f} = \mathbb R\]
Nullstellen der Funktion \(f\) im Intervall \([-3;3]\) ermitteln:
\[\begin{align*}\frac{1}{4}x^{3} + \frac{1}{2}x^{2} - 2x &= 0 \\[0.8em] \frac{1}{4}x (x^{2} + 2x - 8) &= 0 \end{align*}\]
\[x_{1} = 0 \enspace \vee \enspace x^{2} + 2x - 8 = 0\]
Lösungsformel für quadratische Gleichungen anwenden (vgl. Abiturskript - 1.1.2 Quadratische Funktion):
\[x^{2} + 2x - 8 = 0\]
\[\begin{align*}x_{1,2} &= \frac{-2 \pm \sqrt{2^{2} - 4 \cdot 1 \cdot (-8)}}{2 \cdot 1} \\[0.8em] &= \frac{-2 \pm \sqrt{36}}{2} \\[0.8em] &= \frac{-2 \pm 6}{2} \end{align*}\]
\[x_{2} = 2\,; \enspace x_{3} = -4\]
Im Intervall \([-3;3]\) besitzt die Funktion \(f\) die beiden einfachen Nullstellen \(x_{1} = 0\) und \(x_{2} = 2\).
Ohne zu untersuchen, in welchen Teilintervallen der Graph der Funktion \(f\) oberhalb bzw. unterhalb der \(x\)-Achse verläuft, wird für alle bestimmten Integrale der zu berechnenden Teilflächen der Betrag gewählt.
\[A= \left| \int_{-3}^{0} f(x)\,dx\, \right| + \left| \int_{0}^{2} f(x)\,dx\, \right| + \left| \int_{2}^{3} f(x)\,dx\, \right|\]
Stammfunktion \(F\) der Funktion \(f\) bilden:
\[f(x) = \frac{1}{4}x^{3} + \frac{1}{2}x^{2} - 2x\]
Der Funktionsterm \(F(x)\) der Menge aller Stammfunktionen von \(f\) kann mithilfe des unbestimmten Integrals \(\displaystyle \int x^{r} dx = \frac{x^{r + 1}}{r + 1} + C\) formuliert werden (vgl. Abiturskript - 1.6.2 Unbestimmtes Integral, Wichtige unbestimmte Integrale).
\[\begin{align*} F(x) &= \frac{1}{4} \cdot \frac{1}{3 + 1} \cdot x^{3 + 1} + \frac{1}{2} \cdot \frac{1}{2 + 1} \cdot x^{2 + 1} - 2 \cdot \frac{1}{1 + 1} \cdot x^{1 + 1} + C \\[0.8em] &= \frac{1}{4} \cdot \frac{1}{4}x^{4} + \frac{1}{2} \cdot \frac{1}{3}x^{3} - 2 \cdot \frac{1}{2}x^{2} + C \\[0.8em] &= \frac{1}{16}x^{4} + \frac{1}{6}x^{3} - x^{2} + C \end{align*}\]
\(\displaystyle \Longrightarrow \quad F_{0}(x) = \frac{1}{16}x^{4} + \frac{1}{6}x^{3} - x^{2}\) ist eine Stammfunktion der Funktion \(f\) (für \(C = 0\)).
Flächeninhalt \(A\) berechnen:
\[\begin{align*} A \enspace = \qquad &\left| \int_{-3}^{0} f(x)\,dx\, \right| + \left| \int_{0}^{2} f(x)\,dx\, \right| + \left| \int_{2}^{3} f(x)\,dx\, \right| \\[0.8em] \enspace = \qquad &\left| \left[ \frac{1}{16}x^{4} + \frac{1}{6}x^{3} - x^{2} \right]_{-3}^{0} \right| \\[0.8em]+ \enspace &\left| \left[ \frac{1}{16}x^{4} + \frac{1}{6}x^{3} - x^{2} \right]_{0}^{2} \right| \\[0.8em] + \enspace &\left| \left[ \frac{1}{16}x^{4} + \frac{1}{6}x^{3} - x^{2} \right]_{2}^{3} \right| \\[0.8em] \enspace = \qquad &\left| \frac{1}{16} \cdot 0^{4} + \frac{1}{6} \cdot 0^{3} - 0^{2} - \left( \frac{1}{16} \cdot (-3)^{4} + \frac{1}{6} \cdot (-3)^{3} - (-3)^{2} \right) \right| \\[0.8em] + \enspace &\left| \frac{1}{16} \cdot 2^{4} + \frac{1}{6} \cdot 2^{3} - 2^{2} - \left( \frac{1}{16} \cdot 0^{4} + \frac{1}{6} \cdot 0^{3} - 0^{2} \right) \right| \\[0.8em] + \enspace &\left| \frac{1}{16} \cdot 3^{4} + \frac{1}{6} \cdot 3^{3} - 3^{2} - \left( \frac{1}{16} \cdot 2^{4} + \frac{1}{6} \cdot 2^{3} - 2^{2} \right) \right| \\[0.8em] \enspace = \qquad & \left| 0 - \left( \frac{81}{16} - \frac{9}{2} - 9 \right) \right| \\[0.8em] + \enspace &\left| 1 + \frac{4}{3} - 4 - 0 \right| \\[0.8em] + \enspace &\left| \frac{81}{16} + \frac{9}{2} - 9 - \left( 1 + \frac{4}{3} - 4 \right) \right| \\[0.8em] \enspace = \qquad &\left| \frac{135}{16} \right| + \left| -\frac{5}{3} \right| + \left| \frac{107}{48} \right| \\[0.8em] \enspace = \qquad &\frac{37}{3} \approx 12{,}3 \end{align*}\]
![Fläche, die der Graph der Funktion f im Intervall [-3;3] mit der x-Achse einschließt Fläche, die der Graph der Funktion f im Intervall [-3;3] mit der x-Achse einschließt](/images/stories/abi_check/analysis/Int_Flaechenberechnung4.png)
Fläche, die der Graph der Funktion \(f \colon x \mapsto \frac{1}{4}x^{3} + \frac{1}{2}x^{2} - 2x\) für \(x \in [-3;3]\) mit der \(x\)-Achse einschließt.
Flächeninhalt zwischen zwei Funktionsgraphen
Für die Berechnung des Flächeninhalts der Fläche zwischen den Graphen zweier Funktionen \(f\) und \(g\) im Intervall \([a;b]\) wird über die Differenzfunktion \(f(x) - g(x)\) bzw. \(g(x) - f(x)\) integriert. Dabei ist es unerheblich, ob die von den Graphen eingeschlossene Fläche ganz oder teilweise ober- bzw. unterhalb der \(x\)-Achse liegt.
Schneiden sich die Graphen mehrmals im Intervall \([a;b]\), müssen die Teilflächen getrennt betrachtet werden. Hierfür bestimmt man die Schnittstellen \(x_{1}, x_{2}, ..., x_{n}\) der Funktionsgraphen. Sie liefern die Integrationsgrenzen für die bestimmten Integrale der zu berechnenden Teilflächen.
Um jeweils einen positiven Wert für den Flächeninhalt der Teilflächen zu berechnen, wählt man für alle bestimmten Integrale der zu berechnenden Teilflächen den Betrag. Eine Untersuchung, ob der Graph \(G_{f}\) oberhalb des Graphen \(G_{g}\) verläuft oder umgekehrt, kann damit entfallen.
Der Flächeninhalt \(A\) der Fläche zwischen den Graphen zweier Funktionen \(f\) und \(g\) im Intervall \([a;b]\) ist gleich der Summe der Flächeninhalte der Teilflächen \(A_{1}, A_{2}, ... ,A_{n}\).
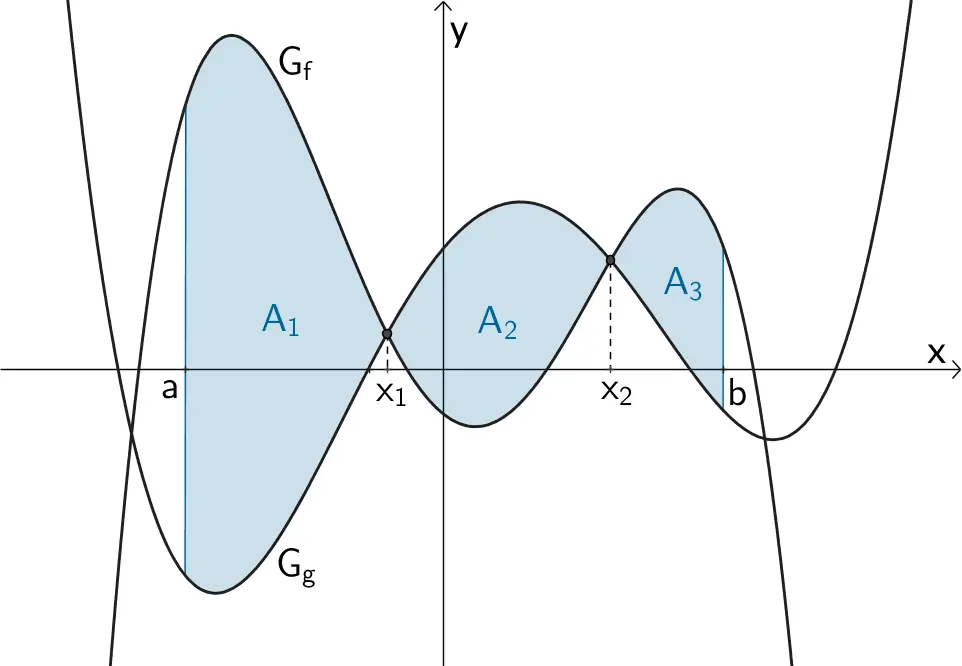
Beispiel: Flächeninhalte \(A_{1}\), \(A_{2}\) und \(A_{3}\), die \(G_{f}\) und \(G_{g}\) im Intervall \([a;b]\) einschließen.
\[\begin{align*} A \enspace = \qquad &A_{1} + A_{2} + ... + A_{n} \\[0.8em] \enspace = \qquad &\left| \int_{a}^{x_{1}} (f(x) - g(x)) \,dx \, \right| \\[0.8em] + \enspace &\left| \int_{x_{1}}^{x_{2}} (f(x) - g(x)) \,dx\, \right| +\; ... \\[0.8em] + \enspace &\left| \int_{x_{n}}^{b} (f(x) - g(x)) \,dx\, \right| \end{align*}\]
Beispiel:
Berechnen Sie den Flächeninhalt \(A\) der Fläche, welche die Graphen der in Funktionen \(f(x) = -x^{2}+4x\) und \(g(x) = x^{3} - 6x^{2} + 8x\) einschließen.
\[f(x) = .x^{2} + 4x\,; \enspace D_{f} = \mathbb R\]
\[g(x) = x^{3} - 6x^{2} + 8x\,; \enspace D_{g} = \mathbb R\]
Schnittstellen der Graphen \(G_{f}\) und \(G_{g}\) berechnen:
\[\begin{align*} f(x) &= g(x) \\[0.8em] -x^{2} + 4x &= x^{3} - 6x^{2} + 8x & &| + x^{2} - 4x \\[0.8em] 0 &= x^{3} - 5x^{2} + 4x \\[0.8em] 0 &= x(x^{2} - 5x + 4) \end{align*}\]
\[x_{1} = 0 \enspace \vee \enspace x^{2} - 5x + 4 = 0\]
Lösungsformel für quadratische Gleichungen anwenden (vgl. Abiturskript - 1.1.2 Quadratische Funktion):
\[x^{2} - 5x + 4 = 0\]
\[\begin{align*} x_{2,3} &= \frac{5 \pm \sqrt{(-5)^{2} - 4 \cdot 1 \cdot 4}}{2 \cdot 1} \\[0.8em] &= \frac{5 \pm 3}{2} \end{align*}\]
\[x_{2} = 1\,; \enspace x_{3} = 4\]
Die Graphen der Funktionen \(f\) und \(g\) schneiden sich an den Stellen \(x_{1} = 0\), \(x_{2} = 1\) und \(x_{3} = 4\).
Damit ergibt sich der Flächeninhalt \(A\) der Fläche, welche die Graphen der in Funktionen \(f\) und \(g\) einschließen zu:
\[A = \left| \int_{0}^{1} (f(x) - g(x))\,dx \right| + \left| \int_{1}^{4} (f(x) - g(x))\,dx \right|\]
Integrandenfunktion (Differenzfunktion) \(f(x) - g(x)\) formulieren:
\[\begin{align*} f(x) - g(x) &= -x^{2} + 4x - (x^{3} - 6x^{2} + 8x) \\[0.8em] \\[0.8em] &= -x^{2} + 4x - x^{3} + 6x^{2} - 8x \\[0.8em] &= -x^{3} + 5x^{2} - 4x \end{align*}\]
Der Funktionsterm \(F(x) - G(x)\) der Menge aller Stammfunktionen von \(f - g\) kann mithilfe des unbestimmten Integrals \(\displaystyle \int x^{r} dx = \frac{x^{r + 1}}{r + 1} + C\) formuliert werden (vgl. Abiturskript - 1.6.2 Unbestimmtes Integral, Wichtige unbestimmte Integrale und Abiturskript - 1.6.1 Stammfunktion, Eigenschaften von Stammfunktionen).
\[\begin{align*} F(x) - G(x) &= -\frac{1}{3 + 1}x^{3 + 1} + 5 \cdot \frac{1}{2 + 1} x^{2 + 1} - 4 \cdot \frac{1}{1 + 1}x^{1 + 1} + C \\[0.8em] &= -\frac{1}{4}x^{4} + \frac{5}{3}x^{3} - 2x^{2} + C \end{align*}\]
\(\displaystyle \Longrightarrow \quad F_{0}(x) - G_{0}(X) = -\frac{1}{4}x^{4} + \frac{5}{3}x^{3} - 2x^{2}\) ist eine Stammfunktion von \(f(x) - g(x)\) (für \(C = 0\)).
Flächeninhalt \(A\) berechnen:
\[\begin{align*} A \enspace = \qquad &\left| \int_{0}^{1} [f(x) - g(x)]\,dx \right| + \left| \int_{1}^{4} [f(x) - g(x)]\,dx \right| \\[0.8em] \enspace = \qquad &\left| \left[ -\frac{1}{4}x^{4} + \frac{5}{3}x^{3} - 2x^{2} \right]_{0}^{1} \right| + \left| \left[ -\frac{1}{4}x^{4} + \frac{5}{3}x^{3} - 2x^{2} \right]_{1}^{4} \right| \\[0.8em] \enspace = \qquad &\left| - \frac{1}{4} \cdot 1^{4} + \frac{5}{3} \cdot 1^{3} - 2 \cdot 1^{2} - \left( -\frac{1}{4} \cdot 0^{4} + \frac{5}{3} \cdot 0^{3} - 2 \cdot 0^{2} \right) \right| \\[0.8em] + \enspace &\left| -\frac{1}{4} \cdot 4^{4} + \frac{5}{3} \cdot 4^{3} - 2 \cdot 4^{2} - \left( -\frac{1}{4} \cdot 1^{4} + \frac{5}{3} \cdot 1^{3} - 2 \cdot 1^{2} \right) \right| \\[0.8em] \enspace = \qquad &\left| -\frac{1}{4} + \frac{5}{3} - 2 - 0 \right| \\[0.8em] + \enspace &\left| -\frac{256}{4} + \frac{320}{3} - 32 - \left( -\frac{1}{4} + \frac{5}{3} - 2 \right) \right| \\[0.8em] \enspace = \qquad &\left| -\frac{7}{12} \right| + \left| \frac{45}{4} \right| \\[0.8em] \enspace = \qquad &\frac{71}{6} \approx 11{,}83 \end{align*}\]
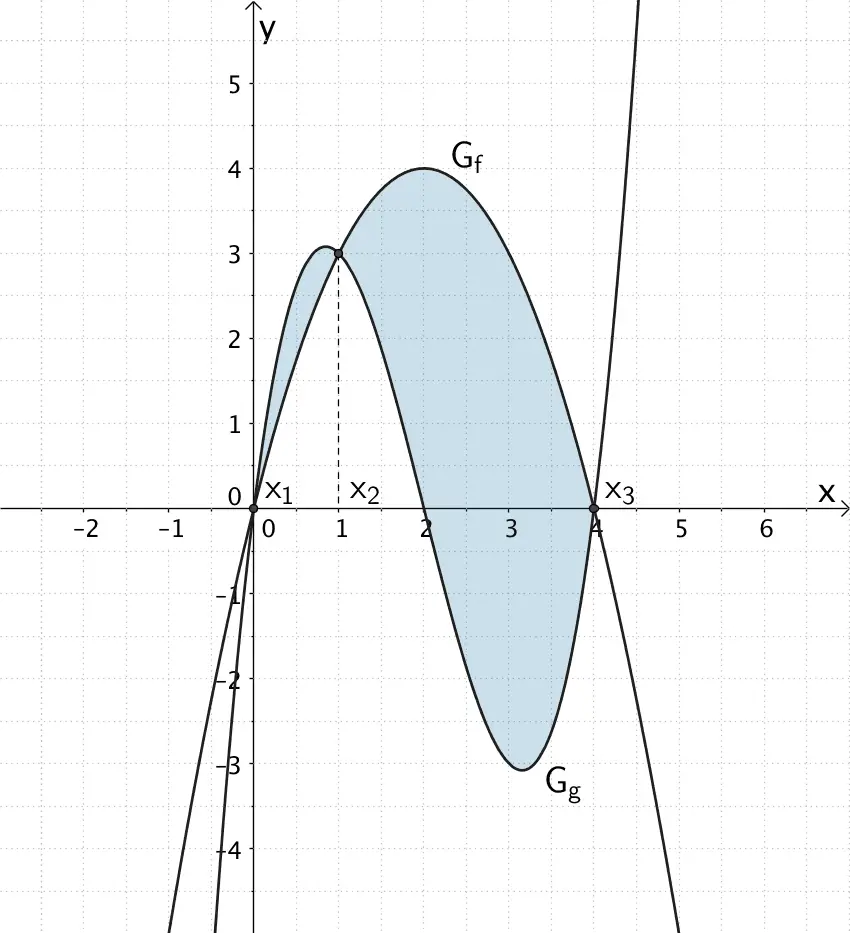
Fläche, welche die Graphen der Funktionen \(f\) und \(g\) einschließen.
Beispielaufgabe
Der Graph der Funktion \(f \colon x \mapsto e^{x}\), die Gerade \(g\) mit der Gleichung \(y = e\) und die Tangente \(T\) an den Graphen der Funktion \(f\) an der Stelle \(x = 0\) schließen ein Flächenstück mit dem Flächeninhalt \(A\) ein.
Zeichnen Sie den Graphen der Funktion \(f\), die Gerade \(g\) und die Tangente \(T\) in ein Koordinatensystem ein und kennzeichnen Sie das Flächenstück mit dem Flächeninhalt \(A\). Berechnen Sie den Flächeninhalt \(A\).
\[f(x) = e^{x}\,; \enspace D_{f} = \mathbb R\]
\[g \colon y = e\]
Einzeichnen von \(G_{f}\), Gerade \(g\) und Tangente \(T\) in ein Koordinatensystem
Die Natürliche Exponentialfunktion \(f \colon x \mapsto e^{x}\) besitzt für \(x \to -\infty\) die \(x\)-Achse (\(y = 0\)) als waagrechte Asymptote und verläuft durch die Punkte \((0|1)\) und \((1|e)\) (vgl. Abiturskript - 1.3.1 Natürliche Exponential- und Logarithmusfunktion, Eigenschaften und Rechenregeln). Die Gerade \(g\) ist eine Parallele zur \(x\)-Achse im Abstand \(e\). Die Tangente \(T\) berührt \(G_{f}\) im Punkt \((0|1)\).
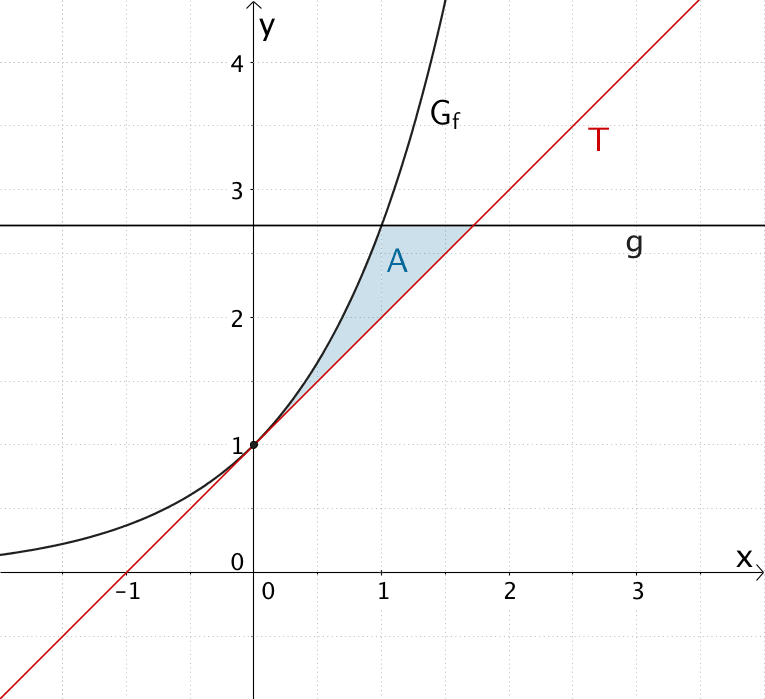
Flächenstück, das \(G_{f}\), die Gerade \(g\) und die Tangente \(T\) einschließen.
Berechnung des Flächeninhalts \(A\)
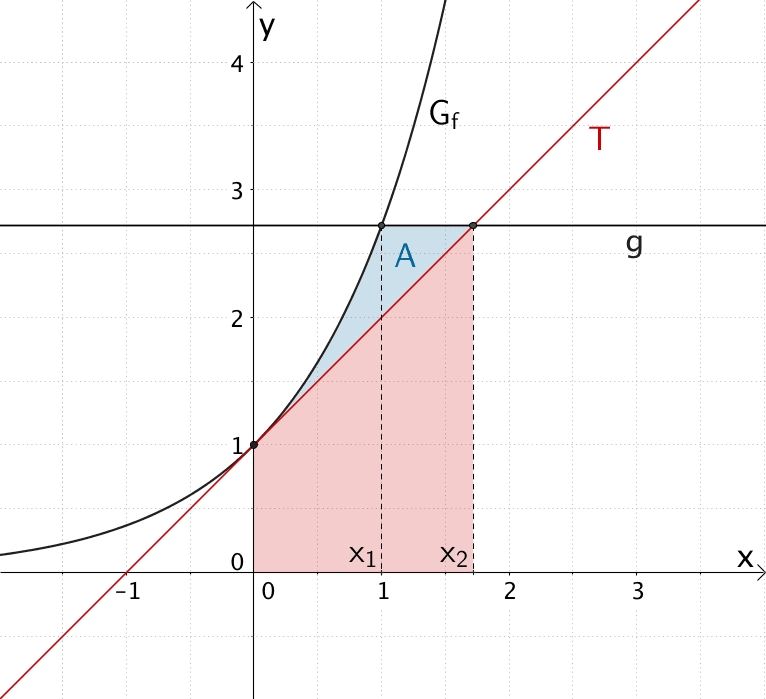
Zunächst wird die Schnittstelle \(x_{1}\) von \(G_{f}\) und der Geraden \(g\) sowie die Schnittstelle \(x_{2}\) der Tangente \(T\) und der Geraden \(g\) ermittelt.
Anschießend berechnet man den Flächeninhalt der Fläche, welche \(G_{f}\) im Intervall \([0;x_{1}]\) mit der \(x\)-Achse einschließt. Hierzu addiert man den Flächeninhalt des Rechtecks, das die Gerade \(g\) im Intervall \([x_{1};x_{2}]\) mit der \(x\)-Achse bildet.
Von diesem Ergebnis subtrahiert man den Flächeninhalt des Trapezes, das die Tangente \(T\) im Intervall \([0;x_{2}]\) mit der \(x\)-Achse bildet und erhält somit den Flächeninhalt \(A\).
\[\begin{align*}A &= \int_{0}^{x_{1}} f(x)\, dx + A_{\text{Rechteck}} - A_{\text{Trapez}} \\[0.8em] &= \int_{0}^{x_{1}}e^{x} dx + e \cdot (x_{2} - x_{1}) - \frac{1 + e}{2} \cdot x_{2}\end{align*}\]
Schnittstelle \(x_{1}\) von \(G_{f}\) und der Geraden \(g\) berechnen:
\[\begin{align*} f(x) &= e \\[0.8em] e^{x} &= e & &| \; \ln \\[0.8em] \ln \left( e^{x} \right) &= \ln e & &| \; \log_{a}\left( a^{x} \right) = x; \; \log_{a} a = 1 \\[0.8em] x &= 1 \end{align*}\]
Der Graph der Funktion \(f\) ud die Gerade \(g\) schneiden sich an der Stelle \(x_{1} = 1\).
Schnittstelle \(x_{2}\) berechnen:
Hierfür wird die Gleichung der Tangente \(T\) benötigt.
\[T \colon y = mx + t\]
\(m = f'(0)\) (vgl. Abiturskript - 1.5.1 Die Ableitung, Tangentensteigung)
Erste Ableitung \(f'\) bilden:
\[f(x) ) = e^{x}\]
\(f'(x) = e^{x}\) (vgl. Abiturskript - 1.5.2 Ableitungsregeln)
\[f'(0) = e^{0} = 1\]
\[\Longrightarrow \quad T \colon y = x + t\]
\[\begin{align*}(0|1) \in T\colon 1 &= 0 + t \\[0.8em] 1 &= t \end{align*}\]
\[\Longrightarrow \quad T \colon y = x + 1\]
\[\begin{align*} T \cap g \colon x + 1 &= e & &| - 1 \\[0.8em] x &= e - 1 \end{align*}\]
Die Tangente \(T\) und die Gerade \(g\) schneiden sich an der Stelle \(x_{2} = e - 1\).
Stammfunktion \(F\) der Funktion \(f\) bilden:
\[f(x) = e^{x}\]
Der Funktionsterm \(F(x)\) der Menge aller Stammfunktionen von \(f\) kann mithilfe des unbestimmten Integrals \(\displaystyle \int e^{x} dx = e^{x} + C\) formuliert werden (vgl. Abiturskript - 1.6.2 Unbestimmtes Integral, Wichtige unbestimmte Integrale).
\[F(x) = e^{x} + C\]
\(\Longrightarrow \quad F_{0}(x) = e^{x}\) ist eine Stammfunktion der Funktion \(f\) (für \(C = 0\)).
Flächeninhalt \(A\) berechnen:
\[x_{1} = 1\,; \enspace x_{2} = e - 1\]
\[\begin{align*}A &= \int_{0}^{x_{1}} f(x)\, dx + A_{\text{Rechteck}} - A_{\text{Trapez}} \\[0.8em] &= \int_{0}^{x_{1}}e^{x} dx + e \cdot (x_{2} - x_{1}) - \frac{1 + e}{2} \cdot x_{2} \\[0.8em] &= \left[ e^{x} \right]_{0}^{1} + e \cdot (e - 1 - 1) - \frac{1 + e}{2} \cdot (e - 1) \\[0.8em] &= e^{1} - e^{0} + e \cdot (e - 2) - \left(\frac{1}{2} + \frac{e}{2}\right) \cdot (e - 1) \\[0.8em] &= e - 1 + e^{2} - 2e - \left( \frac{e}{2} - \frac{1}{2} + \frac{e^{2}}{2} - \frac{e}{2} \right) \\[0.8em] &= e - 1 + e^{2} - 2e + \frac{1}{2} - \frac{e^{2}}{2} \\[0.8em] &= \frac{e^{2}}{2} - e - \frac{1}{2} \\[0.8em] &\approx 0{,}48 \end{align*}\]

