Funktionenschar
Eine Funktionenschar \(f_{k}\) ist einen Menge von Funktionen, deren Funktionsterm \(f_{k}(x)\) neben der Variable \(x\) noch einen veränderlichen Parameter \(k\) enthält. Die Graphen einer Funktionenschar bilden eine Kurvenschar. Zu jedem möglichen Wert des Parameters \(k\) gehört eine Funktion der Schar, auch Scharfunktion genannt. Der Wert des Parameters \(k\) beeinflusst das Verhalten des Graphen einer Scharfunktion, beispielsweise indem er die Lage von Extrempunkten verändert.
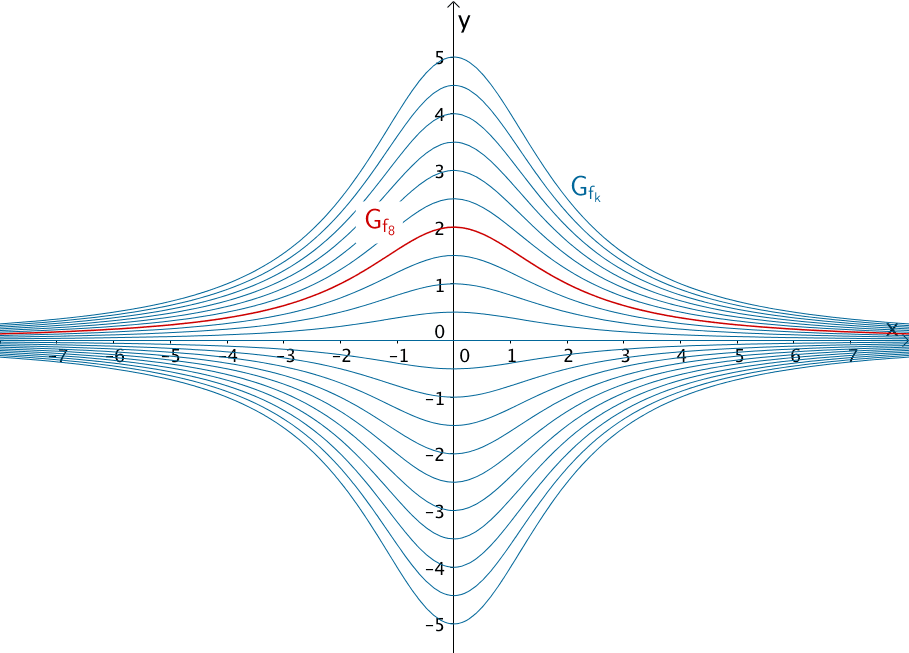
Die Abbildung zeigt die Kurvenschar \(G_{f_{k}}\) der in \(\mathbb R\) definierten Funktionenschar \(f_{k} \colon x \mapsto \dfrac{k}{x^{2} + 4}\) mit \(k \in \mathbb R\). Dargestellt sind die Graphen der Scharfunktionen für \(-20 \leq k \leq 20, \, k \in \mathbb Z\) in Schritten von \(\Delta k = 2 \). Die rote Kurve zeigt z.B. den Graphen \(G_{f_{8}}\) der Scharfunktion \(f_{8} \colon x \mapsto \dfrac{8}{x^{2} +4}\).
Es wird deutlich, dass der Parameter \(k\) eine Streckung um den Faktor \(k\) in \(y\)-Richtung bewirkt. Für \(k < 0\) entstehen die Graphen der zugehörigen Scharfunktionen zusätzlich durch Spiegelung an der \(x\)-Achse (vgl. Abiturskript - 1.1.7 Entwicklung von Funktionen). Die Lage und Art der auf der \(y\)-Achse liegenden Extrempunkte der Kurvenschar verändert sich dadurch.
Einführende Beispiele
Nachfolgende Beispiele verweisen auf typische Aufgabenstellungen zu Funktionenscharen, welche in den Kapiteln 1.7.2 bis 1.7.7 ausführlich behandelt werden.
1. Beispiel
\[f_{k}(x) = \sin{kx}; \; D_{f_{k}} = \mathbb R, \; k \in \mathbb R\]
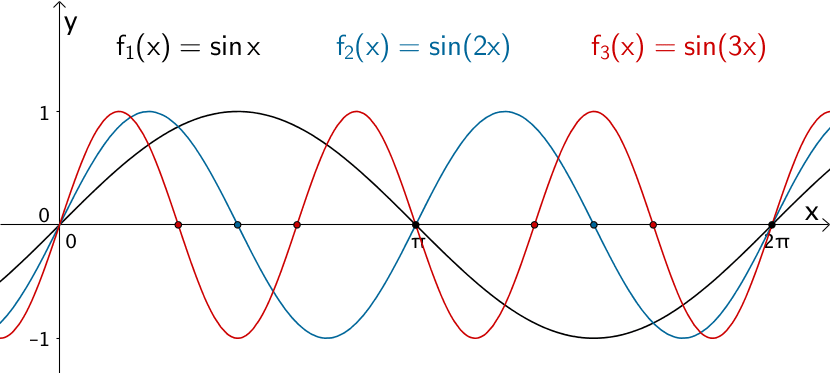
Der Parameter \(k\) der in \(\mathbb R\) definierten Funktionenschar \(f_{k} \colon x \mapsto \sin {(kx)}\) mit \(k \in \mathbb R\) bewirkt eine Streckung/Stauchung des Graphen der Sinusfunktion \(x \mapsto \sin{x}\) in \(x\)-Richtung (vgl. Abiturskript - 1.1.7 Entwicklung von Funktionen). Dadurch ändert sich die Anzahl der Nullstellen der Funktionenschar \(f_{k}\) in einem betrachteten Intervall.
Denkbare Aufgabenstellung:
Für welchen Wert des Parameters \(k\) besitzt der zugehörige Graph der Funktionenschar \(f_{k} \colon x \mapsto \sin{(kx)}\) im Intervall \([0;2\pi]\) genau \(n\) Nullstellen? (vgl. Abiturskript - 1.7.2 Nullstellen einer Funktionenschar)
2. Beispiel
\[f_{k}(x) = 0.25(2k - x)^{2} + k; \; D_{f_{k}} = \mathbb R, \; k \in \mathbb R\]
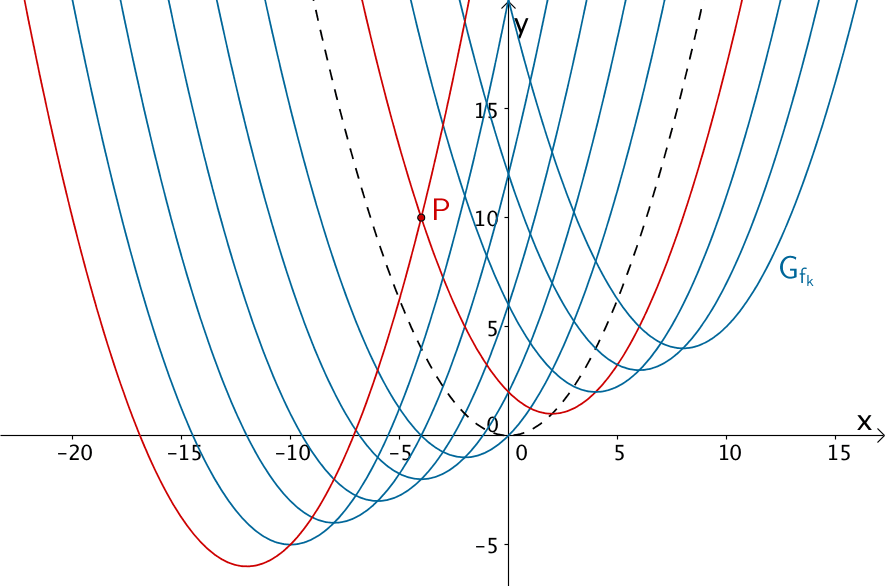
Parabelschar \(g_{f_{k}}\) der in \(\mathbb R\) definierten Funktionenschar \(f_{k} \colon x \mapsto 0{,}25(2k - x)^{2} + k\) mit \(k \in \mathbb R\)
Ausgehend vom Graphen der Funktion \(x \mapsto 0{,}25x^{2}\) (gestrichelte Linie), bewirkt der Parameter \(k\) der Funktionenschar \(f_{k}\) eine Verschiebung in \(x\)-Richtung um \(2k\) und eine Verschiebung in \(y\)-Richtung um \(k\) (vgl. Abiturskript - 1.1.7 Entwicklung von Funktionen).
Denkbare Aufgabenstellung:
Bestimmen Sie diejenigen Werte des Parameters \(k\), sodass die zugehörigen Graphen der Funktionenenschar \(f_{k}\) durch den Punkt \(P(x_{p}|y_{P})\) verlaufen (vgl. Abiturskript - 1.7.3 Graph einer Schaffunktion durch einen Punkt).
3. Beispiel
\[f_{k}(x) = (k + 1) \cdot \sqrt{x - k} + k; \; D_{f_{k}} = [k;+\infty[, \; k > 0\]
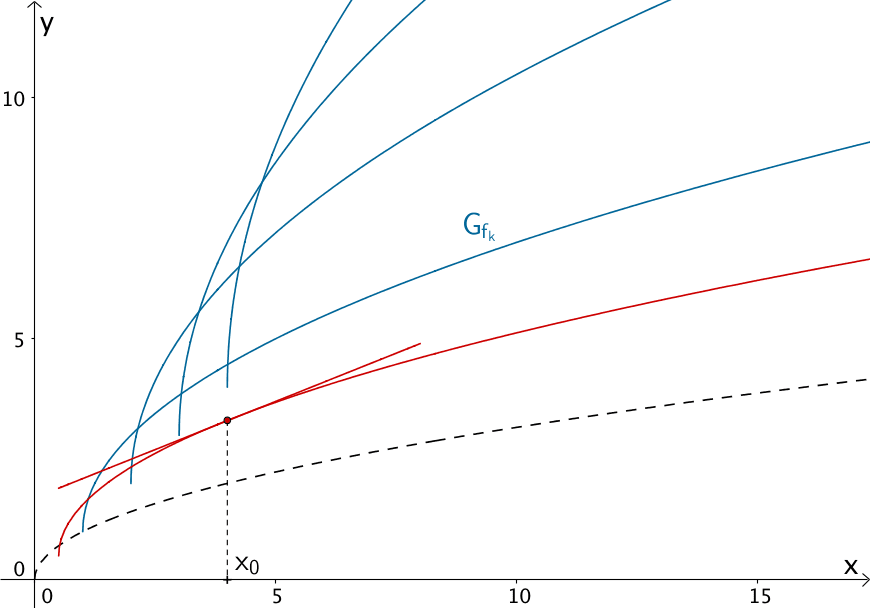
Kurvenschar \(G_{f_{k}}\) der Funktionenschar \(f_{k} \colon x \mapsto (k + 1) \cdot \sqrt{x - k} + k\) mit dem maximalen Definitionsbereich \(D_{f_{k}} = [k;+\infty[\) und \(k \geq 0\)
Ausgehend vom Graphen der Funktion \(x \mapsto \sqrt{x}\) (gestrichelte Linie), bewirkt der Parameter \(k\) der Funktionenschar \(f_{k}\) eine Streckung in \(y\)-Richtung um den Faktor \((k + 1)\) sowie eine Verschiebung in \(x\)-Richtung um \(k\) und eine Verschiebung in \(y\)-Richtung um \(k\) (vgl. Abiturskript - 1.1.7 Entwicklung von Funktionen).
Denkbare Aufgabenstellung:
Ermitteln Sie denjenigen Wert des Parameters \(k\), sodass der zugehörige Graph der Funktionenschar \(f_{k}\) an der Stelle \(x_{0}\) die Steigung \(m\) besitzt (vgl. Abiturskript - 1.7.4 Graph einer Scharfunktion mit vorgegebener Steigung).
4. Beispiel
\[f_{k}(x) = 0{,}5kx^{4} - 4kx^{2}; \; D_{f_{k}} = \mathbb R, \; k > 0\]
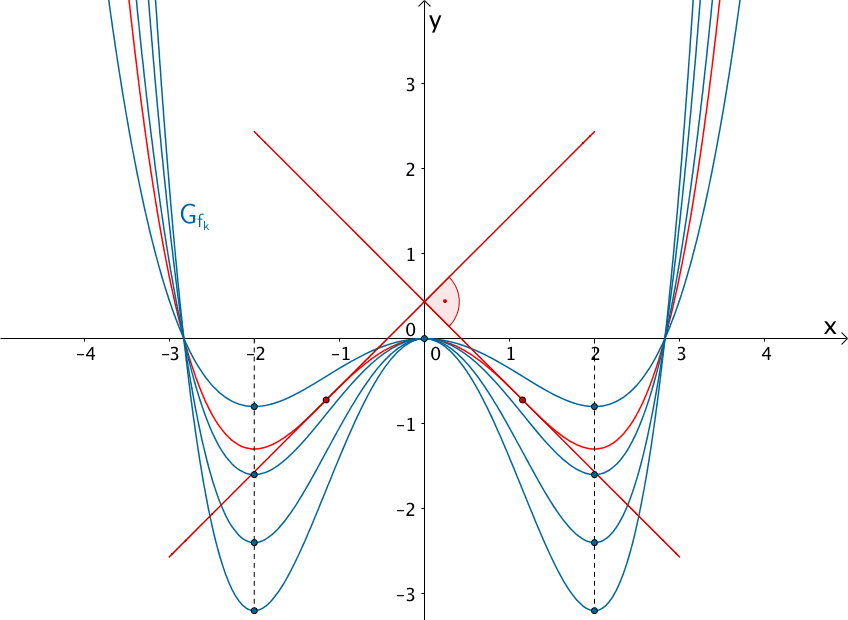
Extremstellen bzw. Extrempunkte sowie orthogonale Wendetangenten der Kurvenschar \(G_{f_{k}}\) der in in \(\mathbb R\) definierten Funktionenschar \(f_{k} \colon x \mapsto 0{,}5kx^{4} - 4kx^{2}\) mit \(k > 0\)
Denkbare Aufgabenstellungen:
a) Zeigen Sie ohne abzuleiten am Funktionsterm \(f_{k}(x)\), dass alle Graphen der Funktionenschar \(f_{k}\) einen Extrempunkt besitzt, dessen Lage unabhängig vom Wert des Parameters \(k\) ist.
b) Weisen Sie nach, dass der Wert des Parameters \(k\) keinen Einfluss auf die Extremstellen der Funktionenschar \(f_{k}\) hat.
c) Für welchen Wert des Parameters \(k\) hat der zugehörige Graph der Funktionenschar \(f_{k}\) zwei zueinander orthogonale Wendetangenten?
(vgl. Abiturskript - 1.7.5 Extrem- / Wendepunkte einer Kurvenschar)
5. Beispiel
\[f_{k}(x) =0{,}5x^{2} + 4kx + 4; \; D_{f_{k}} = \mathbb R, \; k \in \mathbb R\]
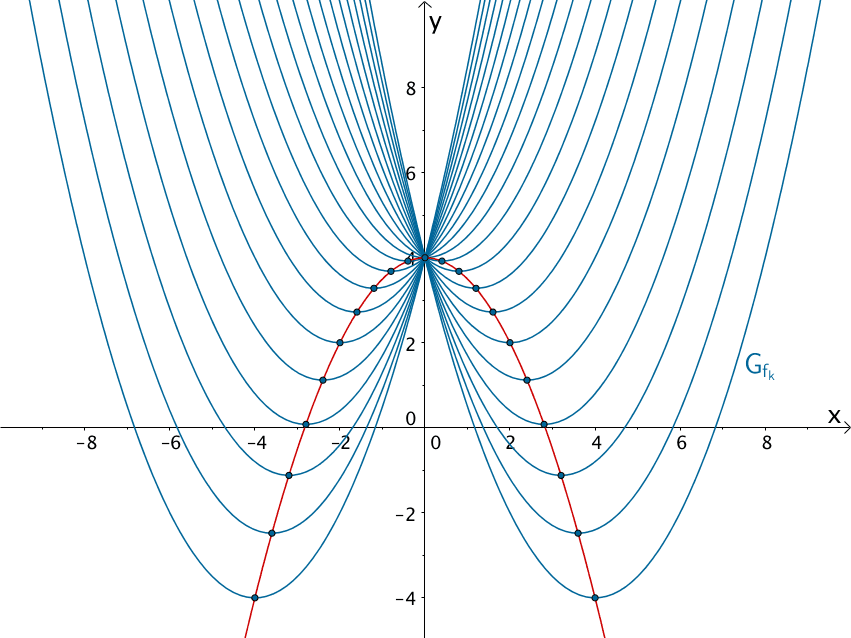
Parabelschar \(G_{f_{k}}\) der in \(\mathbb R\) definierten Funktionenschar \(f_{k} \colon x \mapsto 0{,}5x^{2} +4kx + 4\) mit \(k \in \mathbb R\)
Die Extrempunkte (Scheitelpunkte) der Parabelschar \(G_{f_{k}}\) beschreiben eine nach unten geöffnete Parabel. Sie ist die Ortslinie bzw. der Trägergraph der Extrempunkte der Parabelschar.
Denkbare Aufgabenstellung:
a) Ermitteln Sie die Funktionsgleichung des Graphen, auf dem alle Extrempunkte der Parabelschar der Funktionenschar \(f_{k}\) liegen.
b) Bestimmen Sie denjenigen Wert des Parameters \(k\), für den das Minimum der Parabelschar der Funktionenschar \(f_{k}\) am größten ist.
(vgl. Abiturskript - 1.7.6 Ortslinie / Trägergraph einer Funktionenschar)
6. Beispiel
\[f_{k}(x) = \frac{1}{20}x^{3} + \frac{1}{10}x^{2}\left( 1 - 4k \right) -\frac{2}{5}x\left( 3 + 2k \right) + 192k + 2; \; D_{f_{k}} = \mathbb R, \; k \in \mathbb R\]
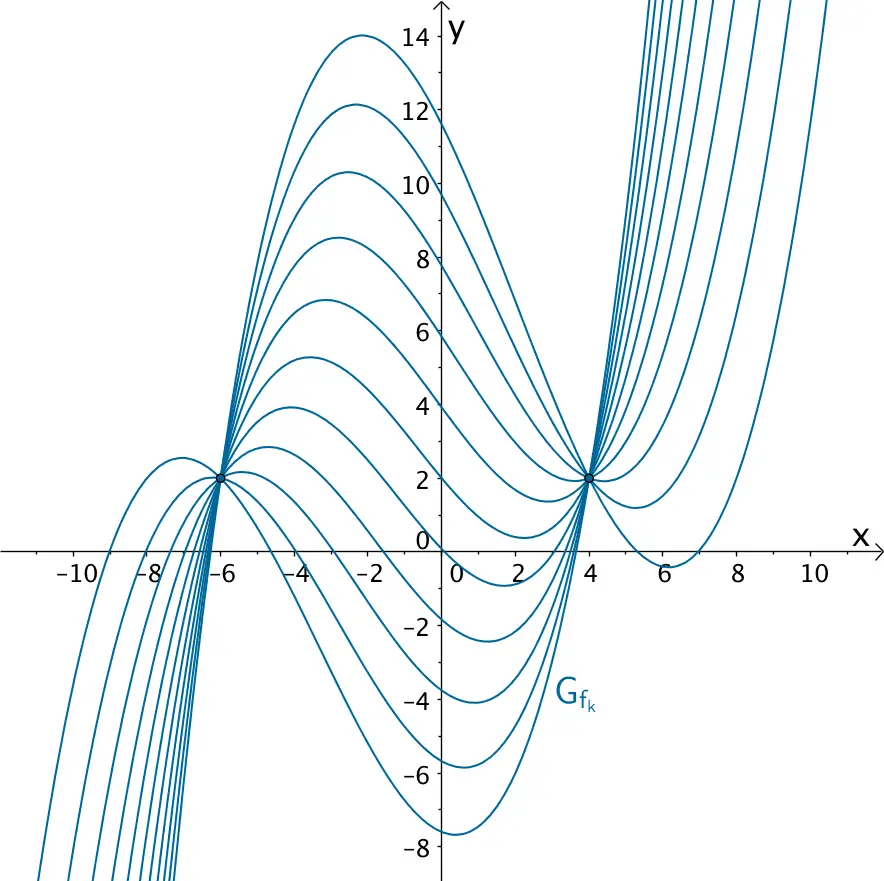
Die Kurvenschar \(G_{f_{k}}\) der in \(\mathbb R\) definierten Funktionenschar \(f_{k} \colon x \mapsto \dfrac{1}{20}x^{3} + \dfrac{1}{10}x^{2}\left( 1 - 4k \right) -\dfrac{2}{5}x\left( 3 + 2k \right) + 192k + 2\) mit \(k \in \mathbb R\) besitzt die gemeinsamen Punkte \((-6|2)\) und \((4|2)\).
Denkbare Aufgabenstellung:
Bestimmen Sie die Koordinaten der gemeinsamen Punkte der Kurvenschar der Funktionenschar \(f_{k}\) (vgl. Abiturskript - 1.7.7 Gemeinsame Punkte einer Kurvenschar).

