Graph einer Scharfunktion durch einen Punkt
Dieser Aufgabentyp betrachtet die Kurvenschar \(G_{f_{k}}\) einer vorliegenden Funktionenschar \(f_{k}\) und fragt nach dem Wert des Parameters \(k\), sodass der Graph der zugehörigen Scharfunktion durch einen gegebenen Punkt \(P(x_{P}|y_{P})\) verläuft.
Die Koordinaten des Punktes \(P\) müssen die Funktionsgleichung \(y = f_{k}(x)\) erfüllen. Es ergibt ich folgender Ansatz:
\[y_{P} = f_{k}(x_{P})\]
Beispiel:
Gegeben sei die in \(\mathbb R^{+}\) definierte Funktionenschar \(f_{k} \colon x \mapsto x \cdot \ln{(kx)}\) mit \(k \in \mathbb R^{+}\).
Bestimmen Sie den Wert des Parameters \(k\) so, dass der Graph der zugehörigen Scharfunktion durch den Punkt \(P(e|e)\) verläuft.
\[f_{k}(x) = x \cdot \ln{(kx)}; \; D_{f_{k}} = \mathbb R^{+}, \; k \in \mathbb R^{+}\]
\[P(e|e)\]
Ansatz formulieren:
\[\begin{align*} y_{P} &= f_{k}(x_{P}) \\[0.8em] e &= e \cdot \ln{(ke)} \end{align*}\]
Die Logarithmusgleichung lässt sich mithilfe der Rechenregeln für Logarithmen lösen (vgl. Abiturskript - 1.3.1 Eigenschaften und Rechenregeln, Natürliche Exponential- und Logarithmusfunktion sowie Abiturskript - 1.3.3 Exponential- und Logarithmusgleichungen).
\[\begin{align*} e &= e \cdot \ln{(ke)} & &| : e \\[0.8em] 1 &= \ln{(ke)} & &| \; \log_{a}{(bc)} = \log_{a}{b} + \log_{a}{c} \\[0.8em] 1 &= \ln{k} + \ln{e} & &| \; \ln{e} = 1 \enspace \left( \text{allg.:} \; \log_{a}{a} = 1 \right) \\[0.8em] 1 &= \ln{k} + 1 & &| - 1 \\[0.8em] 0 &= \ln{k} & &| \; \ln{1} = 0 \enspace \left( \text{allg.:} \; \log_{a}{1} = 0 \right) \\[0.8em] 1 &= k \end{align*}\]
oder:
\[\begin{align*} 0 &= \ln{k} & &| \; e^{(\dots)} \enspace \text{zur Basis} \; e \; \text{potenzieren} \\[0.8em] e^{0} &= e^{\ln{k}} & &| \; a^{0} = 1; \; e^{\ln{x}} = x \enspace \left( \text{allg.:}\; a^{\log_{a}{x}} = x \right) \\[0.8em] 1 &= k \end{align*}\]
Für \(k = 1\) verläuft der Graph der Scharfunktion \(f_{1}\) durch den Punkt \(P(e|e)\).
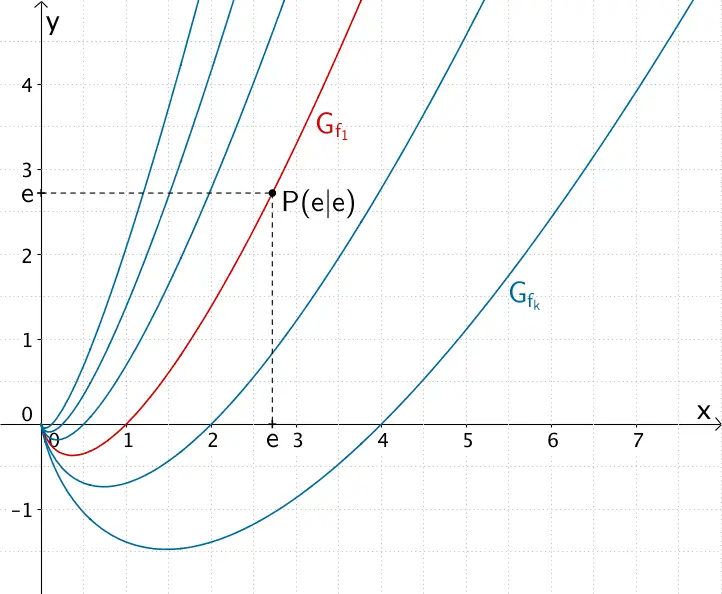
Kurvenschar \(G_{f_{k}}\) der in \( \mathbb R^{+}\) definierten Funktionenschar \(f_{k} \colon x \mapsto x \cdot \ln{(kx)}\) mit \(k \in \mathbb R^{+}\) und Graph \(G_{f_{1}}\) der Scharfunktion \(f_{1}\) durch den Punkt \(P(e|e)\).
Beispielaufgabe
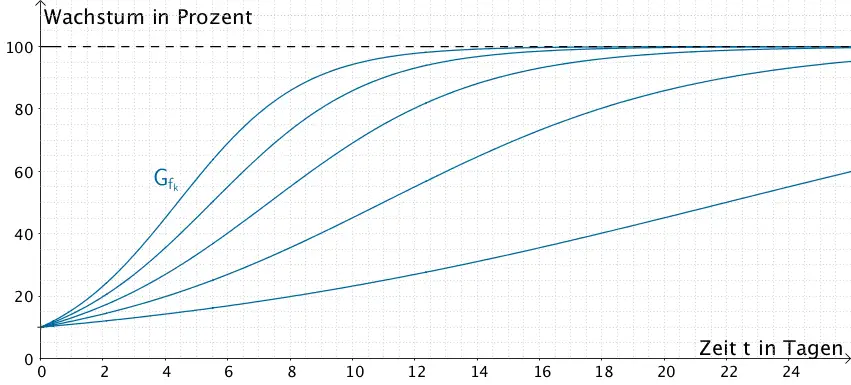
Ein Wachstumsprozess soll näherungsweise mithilfe der Funktionenschar \(f_{k}(t) = 100 \cdot \dfrac{e^{kt}}{e^{kt} + 9}\) mit dem Definitionsbereich \(D_{f_{k}} = \mathbb R^{+}_{0}\) und \(k > 0\) modelliert werden (vgl. Abbildung).
Dabei bedeutet \(t\) die seit Beobachtungsbeginn des Wachstums vergangene Zeit in Tagen und \(f_{k}(t)\) das erreichte Wachstum in Prozent. Der Parameter \(k\) beschreibt eine Wachstumskonstante, welche alle vorhersehbaren Einflussfaktoren, die neben der Zeit \(t\) das Wachstum bestimmen, in sich vereint.
Ermitteln Sie den Wert der Wachstumskonstante \(k\) so, dass der Wachstumsprozess nach 20 Tagen das Achtfache des zu Beginn der Beobachtung vorhandenen Wachstums erreicht.
\[f_{k}(t) = 100 \cdot \frac{e^{kt}}{e^{kt} + 9}; \; D_{f_{k}} = \mathbb R^{+}_{0}, \; k > 0\]
Wachstum zu Beginn der Beobachtung, also zum Zeitpunkt \(t = 0\):
\[\begin{align*}f_{k}(0) &= 100 \cdot \frac{e^{k \cdot 0}}{e^{k \cdot 0} +9} \\[0.8em] &= 100 \cdot \frac{e^{0}}{e^{0} + 9} & &| \; a^{0} = 1 \\[0.8em] &= 100 \cdot \frac{1}{1 + 9} \\[0.8em] &= 10 \end{align*}\]
Zu Beobachtungsbegin \((t = 0)\) beträgt das Wachstum des beobachteten Wachstumsprozesses bereits 10 %.
Nach 20 Tagen soll das Achtfache des zu Beobachtungsbeginn vorhandenen Wachstums erreicht werden, also 80 %. Unter dieser Bedingung ist die Wachstumskonstante \(k\) zu ermitteln.
Mit anderen Worten: Gesucht ist derjenige Wert des Parameters \(k\) der Funktionenschar \(f_{k}\), deren zugehöriger Graph durch den Punkt \((20|80)\) verläuft.
\[\begin{align*} 80 &= f_{k}(20) \\[0.8em] 80 &= 100 \cdot \frac{e^{k \cdot 20}}{e^{k \cdot 20} + 9} & &| : 100 \\[0.8em] 0{,}8 &= \frac{e^{20k}}{e^{20k} + 9} \end{align*}\]
Die Exponentialgleichung lässt sich mithilfe elementare Umformungen und einer sich anschließenden Logarithmieren lösen (vgl. Abiturskript - 1.3.3 Exponential- und Logarithmusgleichungen).
\[\begin{align*} 0{,}8 &= \frac{e^{20k}}{e^{20k} + 9} & &| \cdot (e^{20k} + 9) \\[0.8em] 0{,}8 \cdot (e^{20k} + 9) &= e^{20k} \\[0.8em] 0{,}8 \cdot e^{20k} + 7{,}2 &= e^{20k} & &| - 0{,}8 \cdot e^{20k} \\[0.8em] 7{,}2 &= 0{,}2 \cdot e^{20k} & &| \cdot 5 \\[0.8em] 36 &= e^{20k} & &| \; \ln{(\dots)} \; \text{Logarithmieren} \\[0.8em] \ln{36} &= \ln{\left( e^{20k} \right)} & &| \; \ln{(e^{x})} = x \enspace \left( \text{allg.:} \; \log_{a}(a^{x}) = x \right) \\[0.8em] \ln{36} &= 20k & &| : 20 \\[0.8em] \frac{\ln{36}}{20} &= k \\[0.8em] \frac{\ln{6^{2}}}{20} &= k & &| \; \log_{a}{n^{n}} = n \cdot \log_{a}{b} \\[0.8em] \frac{2\ln{6}}{20} &= k \\[0.8em] \frac{\ln{6}}{10} &= k \\[0.8em] k &\approx 0{,}18 \end{align*}\]
Für \(k = \dfrac{\ln{6}}{10}\) ist der beobachtete Wachstumsprozesses nach 20 Tagen zu 80 % abgeschlossen.
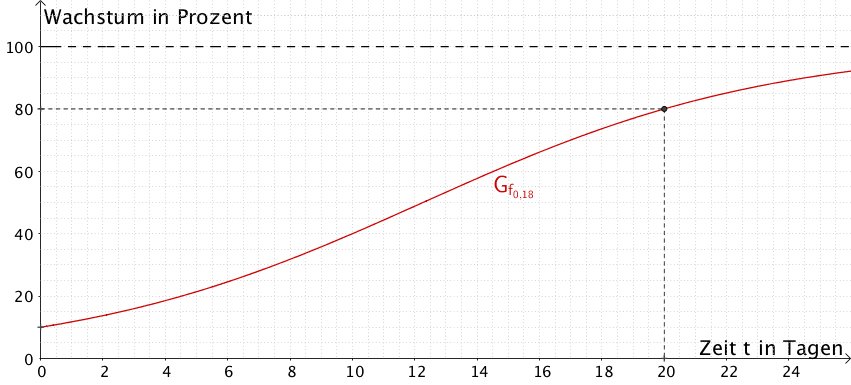
Graph \(G_{f_{0{,}18}}\) der Scharfunktion \(f_{0{,}18} \colon x \mapsto 100 \cdot \dfrac{e^{0{,}18}}{e^{0{,}18t} + 9}\) durch den Punkt \((20|80)\)

