Graph einer Scharfunktion mit vorgegebener Steigung
Es sei eine Gerade \(g\) mit der Steigung \(m\) sowie eine nicht lineare Funktionenschar \(f_{k}\) gegeben. Für welchen Wert des Parameters \(k\) besitzt der zugehörige Graph der Funktionenschar \(f_{k}\) an einer bestimmten Stelle \(x_{0}\) die gleiche Steigung wie die Gerade \(g\)?
Die Steigungen der Kurvenschar an der Stelle \(x_{0}\) entsprechen den Steigungen der Tangenten an die Kurvenschar an der Stelle \(x_{0}\). Die erste Ableitung \(f'_{k}(x_{0})\) beschreibt die Tangentensteigungen der Kurvenschar an der Stelle \(x_{0}\) (vgl. Abiturskript - 1.5.1 Die Ableitung, Tangentensteigung).
Folglich muss an der Stelle \(x_{0}\) gelten:
\[f'_{k}(x_{0}) = m\]
Beispiel:
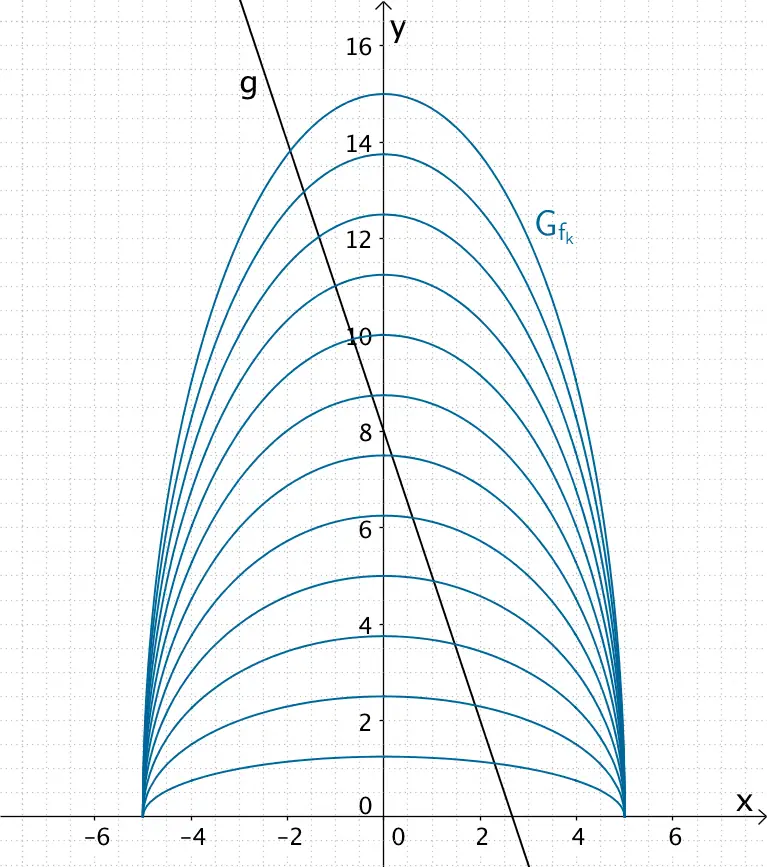
Geben sei die Funktionenschar \(f_{k} \colon x \mapsto k \cdot \sqrt{25 - x^{2}}\) mit dem Definitionsbereich \(D_{f_{k}} = [-5;5]\) und \(k > 0\) sowie die Gerade \(g \colon x \mapsto -3x + 8\) (vgl. Abbildung).
Bestimmen Sie denjenigen Wert des Parameters \(k\), sodass der zugehörige Graph der Funktionenschar \(f_{k}\) an der Stelle \(x_{0} = 4\) die Steigung der Geraden \(g\) besitzt.
\[f_{k}(x) = k \cdot \sqrt{25 - x^{2}}; \; D_{f_{k}} = [-5;5], \; k > 0\]
\[g(x) = -3x + 8\]
\[x_{0} = 4\]
Dem Funktionsterm \(g(x)\) der Geraden \(g\) kann die Steigung zu \(m = -3\) entnommen werden.
Ansatz formulieren:
\[\begin{align*}f'_{k}(x_{0}) &= m \\[0.8em] f'_{k}(4) &= -3 \end{align*}\]
Erste Ableitung \(f'_{k}\) bilden:
Der Funktionsterm \(f_{k}(x)\) lässt sich mithilfe der Faktorregel, der Kettenregel, der Ableitung einer Wurzelfunktion und der Ableitung einer Potenzfunktion ableiten. Als Alternative formuliert man den Funltionsterm \(f_{k}(x)\) vorab in der Potenzschreibweise. Der Parameter \(k\) wird beim Ableiten wie eine Konstante behandelt (vgl. Abiturskript - 1.5.2 Ableitungsregeln).
\[f_{k}(x) = k \cdot \sqrt{25 - x^{2}}\]
\[\begin{align*} f'_{k}(x) &= k \cdot \frac{1}{2\sqrt{25 - x^{2}}} \cdot (-2x) \\[0.8em] &= -\frac{kx}{\sqrt{25 - x^{2}}} \end{align*}\]
oder:
\[\begin{align*}f_{k}(x) &= k \cdot \sqrt{25 - x^{2}} & &| \; \sqrt{a} = a^{\frac{1}{2}} \\[0.8em] &= k \cdot (25 - x^{2})^{\frac{1}{2}} \end{align*}\]
\[\begin{align*}f'_{k}(x) &= k \cdot \frac{1}{2} \cdot (25 - x^{2})^{-\frac{1}{2}} \cdot (-2x) & &| \; a^{\frac{1}{2}} = \sqrt{a}; \; a^{-n} = \frac{1}{a^{n}} \\[0.8em] &= -\frac{kx}{\sqrt{25 - x^{2}}} \end{align*}\]
Wert des Parameters \(k\) berechnen:
\[x_{0} = 4; \enspace m = -3\]
\[\begin{align*}f'_{k}(x_{0}) &= m \\[0.8em] f'_{k}(4) &= -3 \\[0.8em] -\frac{k \cdot 4}{\sqrt{25 - 4^{2}}} &= -3 \\[0.8em] -\frac{4k}{3} &= -3 & &| \cdot (-3) \\[0.8em] 4k &= 9 & &| : 4 \\[0.8em] k &= \frac{9}{4} \\[0.8em] k &= 2{,}25 \end{align*}\]
Für \(k = 2{,}25\) besitzt der Graph der zugehörigen Scharfunktion \(f_{2{,}25}\) an der Stelle \(x_{0} = 4\) die Steigung der Geraden \(g\).
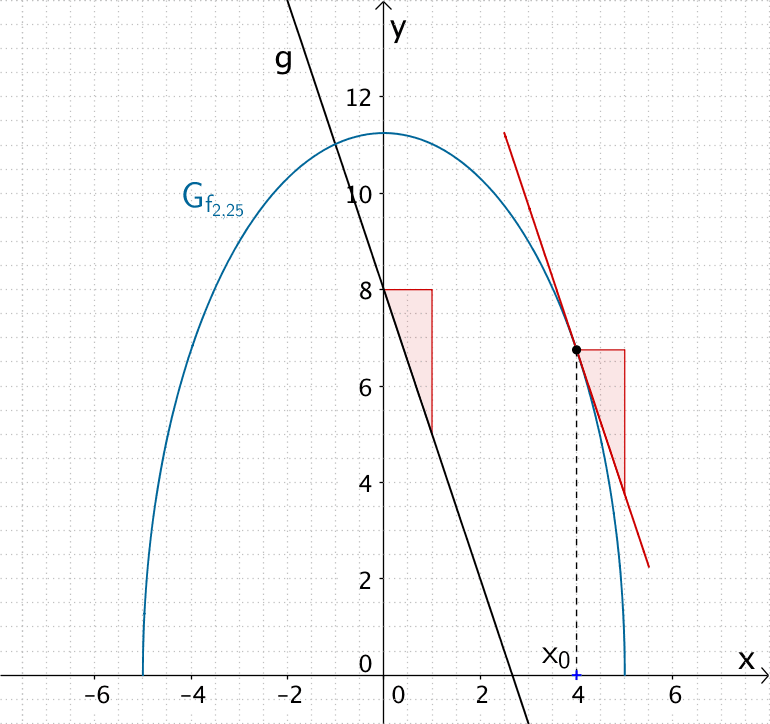
Graph \(G_{f_{2{,}25}}\) der Scharfunktion \(f_{2{,}25} \colon x \mapsto 2{,}25 \cdot \sqrt{25 - x^{2}}\), dessen Steigung an der Stelle \(x_{0} = 4\) gleich der Steigung der Geraden \(g\) ist.
Beispielaufgabe
Gegeben sei die in \(\mathbb R^{+}\) definierte Funktionenschar \(f_{k} \colon x \mapsto kx \cdot \ln{x} + k\) mit \(k > 0\).
Bestimmen Sie den Wert des Parameters \(k\) so, dass die Tangente an den zugehörigen Graphen der Funktionenschar \(f_{k}\) an der Stelle \(x_{0} = 4\) parallel zur Winkelhalbierenden des I. und III Quadranten verläuft.
\[f_{k}(x) = kx \cdot \ln{x} + k; \; D_{f_{k}} = \mathbb R^{+}, \; k > 0\]
Die Tangente an einen Graphen der Funktionenschar \(f_{k}\) verläuft parallel zur Winkelhalbierenden des I. und III. Quadranten, wenn die Steigung \(m_{T}\) der Tangente gleich der Steigung \(m_{W}\) der Winkelhalbierenden ist (vgl. Abiturskript - 1.1.1 Lineare Funktion, parallele Geraden). Es gilt: \(m_{W} = 1\).
Die erste Ableitung \(f'_{k}(x_{0})\) beschreibt die Steigung einer Tangente \(T\) an einen Graphen der Funktionenschar \(f_{k}\) an einer betrachteten Stelle \(x_{0}\) in Abhängigkeit des Parameters \(k\) (vgl. Abiturskript - 1.5.1 Die Ableitung, Tangentensteigung).
Mit \(x_{0} = 4\) folgt:
\[\begin{align*}m_{T} &= m_{W} \\[0.8em] f'_{k}(x_{0}) &= m_{W} \\[0.8em] f'_{k}(4) &= 1 \end{align*}\]
Erste Ableitung \(f'_{k}\) bilden:
Der Funktionsterm \(f_{k}(x)\) kann mithilfe der Produktregel, der Ableitung der Natürlichen Logarithmusfunktion und der Summenregel abgeleitet werden. Der Parameter \(k\) wird beim Ableiten wie eine Konstante behandelt (vgl. Abiturskript - 1.5.2 Ableitungsregeln).
\[\begin{align*}f_{k}(x) &= kx \cdot \ln{x} + k \\[0.8em] &= k \cdot (x \ln{x} + 1 ) \end{align*}\]
\[\begin{align*}f'_{k}(x) &= k \cdot \left( 1 \cdot \ln{x} + x \cdot \frac{1}{x} + 0 \right) \\[0.8em] &= k \cdot (\ln{x} + 1) \end{align*}\]
Wert des Parameters \(k\) berechnen:
\[x_{0} = 4; \enspace m_{W} = 1\]
\[\begin{align*} f'_{k}(x_{0}) &= m_{W} \\[0.8em] k \cdot (\ln{4} + 1) &= 1 & &| : (\ln{4} + 1) \\[0.8em] k &= \frac{1}{\ln{4} + 1} \\[0.8em] k &= \frac{1}{\ln{2^{2}}+ 1} & &| \log_{a}{b^{n}} = n \cdot \log_{a}{b} \\[0.8em] k &= \frac{1}{2\ln{2} + 1} \\[0.8em] k &\approx 0{,}42\end{align*}\]
Für \(k = \dfrac{1}{2\ln2 + 1}\) verläuft die Tangente an den zugehörigen Graphen der Funktionenschar \(f_{k}\) an der Stelle \(x_{0} = 4\) parallel zur Winkelhalbierenden des I. und III. Quadranten.
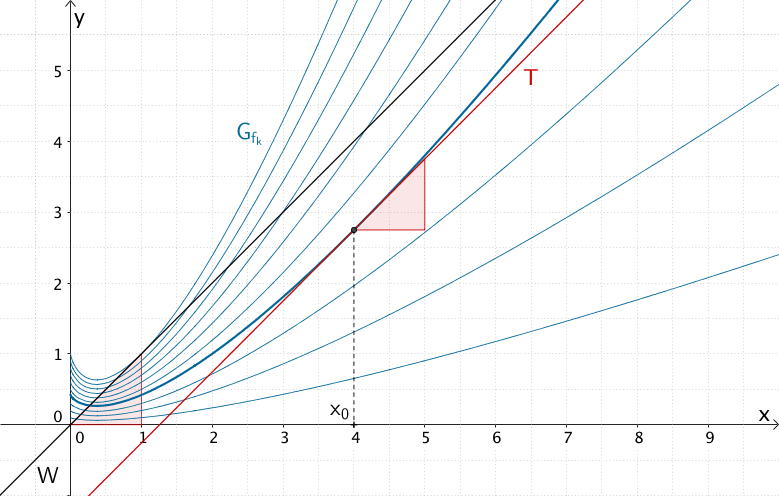
Tangente \(T\) an den für \(k = \dfrac{1}{2\ln2 + 1}\) zugehörigen Graphen der Funktionenschar \(f_{k}\) an der Stelle \(x_{0} = 4\), welche parallel zur Winkelhalbierenden des I. und III, Quadranten ist.

