Die Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) heißen linear abhängig, wenn sich mindestens einer der Vektoren als Linearkombination der anderen Vektoren darstellen lässt. Andernfalls heißen die Vektoren linear unabhängig.
Unter einer Linearkombination der Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) versteht man einen Term der Form \(r \cdot \overrightarrow{a} + s \cdot \overrightarrow{b} + t \cdot \overrightarrow{c}\).
In der Ebene \(\mathbb R^{2}\) sind höchstens zwei Vektoren linear unabhängig.
Im Raum \(\mathbb R^{3}\) sind höchstens drei Vektoren linear unabhängig.
Jeder weitere Vektor lässt sich eindeutig als Linearkombination der linear unabhängigen Vektoren darstellen.
Lineare (Un-)Abhängigkeit von zwei Vektoren
Zwei Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) sind
linear abhängig, wenn
\(\overrightarrow{a} \parallel \overrightarrow{b}\quad\) bzw. \(\quad\overrightarrow{a} = k \cdot \overrightarrow{b}\,; \enspace k \in \mathbb R \quad\) gilt.
linear unabhängig, wenn
\(\overrightarrow{a} \nparallel \overrightarrow{b}\quad\) bzw. \(\quad\overrightarrow{a} \neq k \cdot \overrightarrow{b}\,; \enspace k \in \mathbb R \quad\) gilt.
Lineare (Un-)Abhängigkeit von drei Vektoren
Drei Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) sind
linear abhängig, wenn
sie in einer Ebene liegen bzw. wenn
die lineare Vektorgleichung \(\overrightarrow{c} = r \cdot \overrightarrow{a} + s \cdot \overrightarrow{b}\) eine eindeutige Lösung hat.
linear unabhängig, wenn
sie den Raum \(\mathbb R^{3}\) aufspannen bzw. wenn
die lineare Vektorgleichung \(\overrightarrow{c} = r \cdot \overrightarrow{a} + s \cdot \overrightarrow{b}\) keine Lösung hat.
Bei der Untersuchung der linearen (Un)Abhängigkeit dreier Vektoren spielt es keine Rolle, welche der drei Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) oder \(\overrightarrow{c}\) man als Linearkombination der beiden anderen Vektoren darzustellen versucht.
Beispiel:
Gegeben seien die Vektoren \(\overrightarrow{a} = \begin{pmatrix} 3 \\ 4 \\ 7 \end{pmatrix}\), \(\overrightarrow{b} = \begin{pmatrix} 2 \\ -2 \\ 5 \end{pmatrix}\), \(\overrightarrow{c} = \begin{pmatrix} 1 \\ -8 \\ 3 \end{pmatrix}\) und \(\overrightarrow{d} = \begin{pmatrix} 5 \\ -2 \\ -4 \end{pmatrix}\).
Zeigen Sie rechnerisch, dass
a) die Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) linear abhängig sind.
b) die Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{d}\) linear unabhängig sind.
a) Nachweis, dass die Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) linear abhängig sind
\(\overrightarrow{a} = \begin{pmatrix} 3 \\ 4 \\ 7 \end{pmatrix}\), \(\overrightarrow{b} = \begin{pmatrix} 2 \\ -2 \\ 5 \end{pmatrix}\), \(\overrightarrow{c} = \begin{pmatrix} 1 \\ -8 \\ 3 \end{pmatrix}\)
Je zwei der drei Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) sind linear unabhängig, denn kein Vektor lässt sich durch ein (skalares) Vielfaches von einem anderen Vektor darstellen.
Die Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) sind linear abhängig, wenn beispielsweise die lineare Vektorgleichung \(\overrightarrow{c} = r \cdot \overrightarrow{a} + s \cdot \overrightarrow{b}\) eine eindeutige Lösung hat, wenn sich also der Vektor \(\overrightarrow{c}\) als Linearkombination \(r \cdot \overrightarrow{a} + s \cdot \overrightarrow{b}\) der Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) darstellen lässt.
\[\begin{pmatrix} 1 \\ -8 \\ 3 \end{pmatrix} = r \cdot \begin{pmatrix} 3 \\ 4 \\ 7 \end{pmatrix} + s \begin{pmatrix} 2 \\ -2 \\ 5 \end{pmatrix}\]
Lineares Gleichungssystem formulieren:
\[\begin{align*} \text{I} & & & \quad \: 1 = 3r + 2s \\[0.8em] \text{II} & & \wedge \enspace & -8 = 4r - 2s \\[0.8em] \text{III} & &\wedge \enspace & \quad \: 3 = 7r + 5s \end{align*}\]
Gleichungssystem lösen, z.B. mit dem Additionsverfahren:
\[\begin{align*} \text{I} + \text{II} \colon \; -7 &= 7r & &| : 7 \\[0.8em] -1 &= r \end{align*}\]
\[\begin{align*} r = -1 \; \text{in I} \colon \; 1 &= 3 \cdot (-1) + 2s \\[0.8em] 1 &= -3 + 2s & &| + 3 \\[0.8em] 4 &= 2s & &| : 2 \\[0.8em] 2 &= s \end{align*}\]
\[\begin{align*} r = -1, s = 2 \; \text{in III}\colon \; 3 &= 7 \cdot (-1) + 5 \cdot 2 \\[0.8em] 3 &= -7 + 10 \\[0.8em] 3 &= 3 \quad (\text{w}) \end{align*}\]
\[\Longrightarrow \quad \overrightarrow{c} = (-1) \cdot \overrightarrow{a} + 2 \cdot \overrightarrow{b}\]
\(\Longrightarrow \quad\)Die Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) sind linear abhängig.
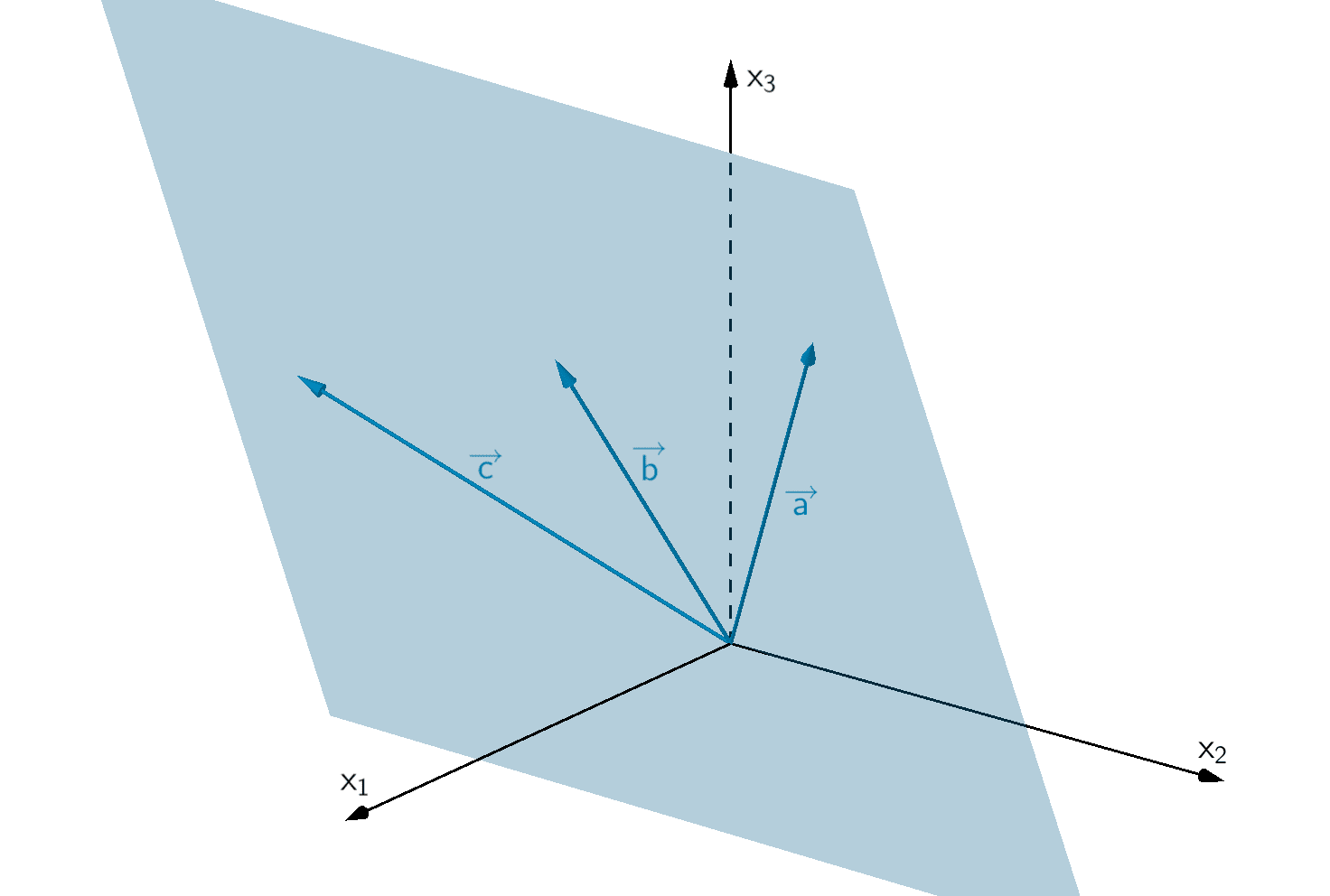
Die drei linear abhängigen Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) liegen in einer Ebene.
b) Nachweis, dass die Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{d}\) linear unabhängig sind
\(\overrightarrow{a} = \begin{pmatrix} 3 \\ 4 \\ 7 \end{pmatrix}\), \(\overrightarrow{b} = \begin{pmatrix} 2 \\ -2 \\ 5 \end{pmatrix}\), \(\overrightarrow{d} = \begin{pmatrix} 5 \\ -2 \\ -4 \end{pmatrix}\)
Je zwei der drei Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{d}\) sind linear unabhängig, denn kein Vektor lässt sich durch ein (skalares) Vielfaches von einem anderen Vektor darstellen.
Die Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{d}\) sind linear unabhängig, wenn beispielsweise die lineare Vektorgleichung \(\overrightarrow{d} = r \cdot \overrightarrow{a} + s \cdot \overrightarrow{b}\) keine Lösung hat, wenn sich also der Vektor \(\overrightarrow{d}\) nicht als Linearkombination \(r \cdot \overrightarrow{a} + s \cdot \overrightarrow{b}\) der Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) darstellen lässt.
\[\begin{pmatrix} 5 \\ -2 \\ -4 \end{pmatrix} = r \cdot \begin{pmatrix} 3 \\ 4 \\ 7 \end{pmatrix} + s \begin{pmatrix} 2 \\ -2 \\ 5 \end{pmatrix}\]
Lineares Gleichungssystem formulieren:
\[\begin{align*} \text{I} & & & \quad \: 5 = 3r + 2s \\[0.8em] \text{II} & & \wedge \enspace & -2 = 4r - 2s \\[0.8em] \text{III} & &\wedge \enspace & -4 = 7r + 5s \end{align*}\]
Gleichungssystem lösen, z.B. mit dem Additionsverfahren:
\[\begin{align*} \text{I} + \text{II} \colon \; 3 &= 7r & &| : 7 \\[0.8em] \frac{3}{7} &= r \end{align*}\]
\[\begin{align*} r = \frac{3}{7} \; \text{in I} \colon \; 5 &= 3 \cdot \frac{3}{7} + 2s \\[0.8em] 5 &= \frac{9}{7} + 2s & &| - \frac{9}{7} \\[0.8em] \frac{26}{7} &= 2s & &| : 2 \\[0.8em] \frac{13}{7} &= s \end{align*}\]
\[\begin{align*} r = \frac{3}{7}, s = \frac{13}{7} \; \text{in III}\colon \; -4 &= 7 \cdot \frac{3}{7} + 5 \cdot \frac{13}{7} \quad (\text{f}) \end{align*}\]
\(\Longrightarrow \quad\)Es existiert keine Lösung.
\(\Longrightarrow \quad\)Die Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{d}\) sind linear unabhängig.
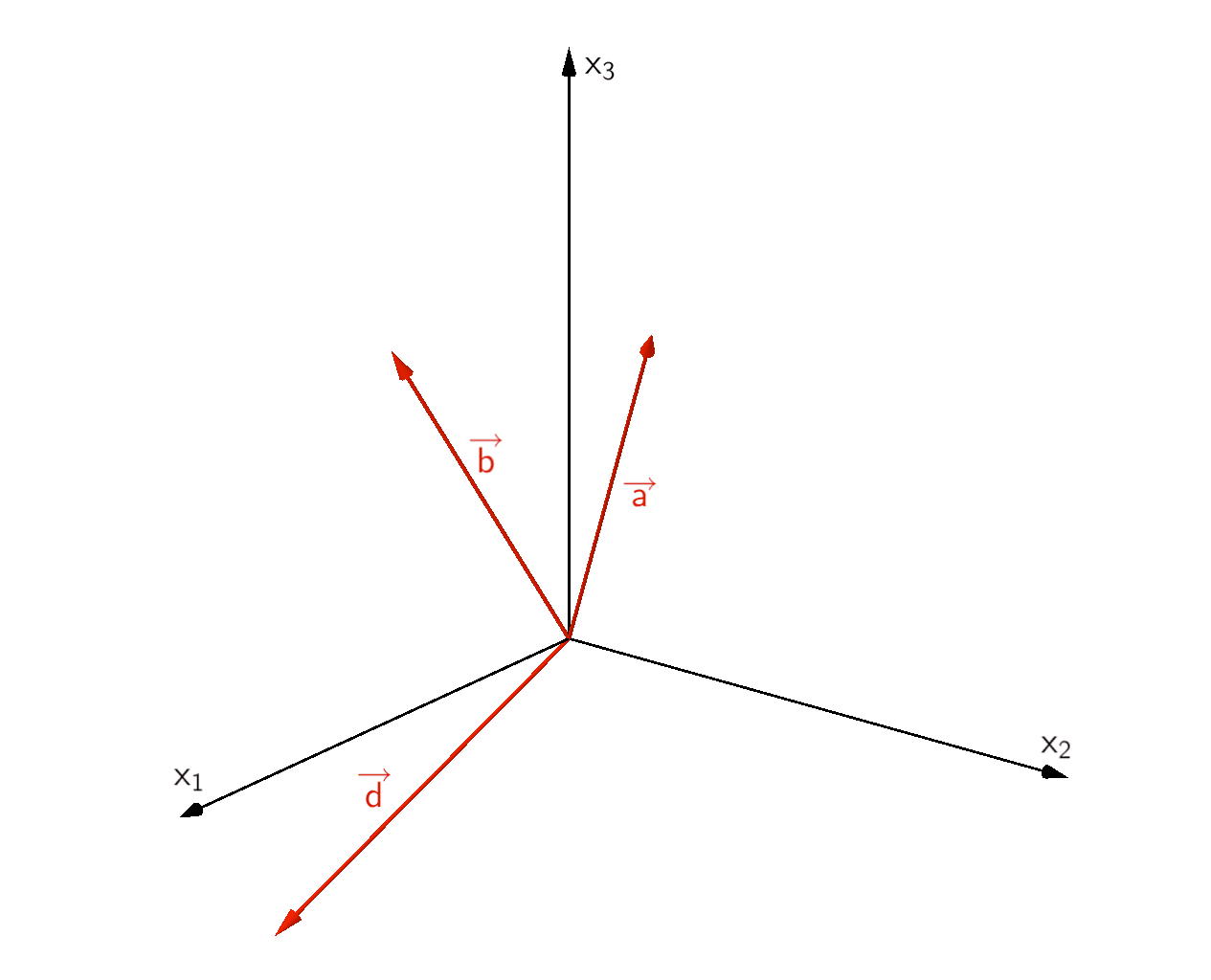
Die drei linear unabhängigen Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{d}\) spannen den Raum \(\mathbb R^{3}\) auf.
Beispielaufgabe
Gegeben seien die Vektoren \(\overrightarrow{a} = \begin{pmatrix} t \\ 2 \\ 3 \end{pmatrix}\) mit \(t \in \mathbb R\), \(\overrightarrow{b} = \begin{pmatrix} -4 \\ 3 \\ 1 \end{pmatrix}\) und \(\overrightarrow{c} = \begin{pmatrix} 6 \\ -5 \\ 3 \end{pmatrix}\).
Bestimmen Sie den Wert des Parameters \(t\) so, dass die drei Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) in einer Ebene liegen, also linear abhängig sind.
Die Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) sind linear abhängig, wenn beispielsweise die lineare Vektorgleichung \(\overrightarrow{a} = r \cdot \overrightarrow{b} + s \cdot \overrightarrow{c}\) eine eindeutige Lösung hat, wenn sich also der Vektor \(\overrightarrow{a}\) als Linearkombination \(r \cdot \overrightarrow{b} + s \cdot \overrightarrow{c}\) der Vektoren \(\overrightarrow{b}\) und \(\overrightarrow{c}\) darstellen lässt.
\[\begin{pmatrix} t \\ 2 \\ 3 \end{pmatrix} = r \cdot \begin{pmatrix} -4 \\ 3 \\ 1 \end{pmatrix} + s \begin{pmatrix} 6 \\ -5 \\ 3 \end{pmatrix}\]
Lineares Gleichungssystem formulieren:
\[\begin{align*} \text{I} & & & \, t = -4r + 6s \\[0.8em] \text{II} & & \wedge \enspace & 2 = \enspace \; 3r - 5s \\[0.8em] \text{III} & &\wedge \enspace & 3 = \quad \; r + 3s \end{align*}\]
Gleichungssystem lösen, z.B. mit dem Additionsverfahren:
In diesem Fall führt beispielsweise der Rechenschritt \(3 \cdot \text{III} - \text{II}\) auf eine Gleichung, die nur noch die Unbekannte \(s\) enthält.
\[\begin{align*}3 \cdot \text{III} - \text{II} \colon \; 3 \cdot 3 - 2 &= 3r - 3r + 3 \cdot 3s - (-5s) \\[0.8em] 7 &= 14s & & | : 14 \\[0.8em] \frac{1}{2} &= s \end{align*}\]
\[\begin{align*} s = \frac{1}{2} \; \text{in III} \colon \; 3 &= r + 3 \cdot \frac{1}{2} \\[0.8em] 3 &= r + \frac{3}{2} & &| - \frac{3}{2} \\[0.8em] \frac{3}{2} &= r \end{align*}\]
\[\begin{align*} r = \frac{3}{2}, s = \frac{1}{2} \; \text{in I}\colon \; t &= -4 \cdot \frac{3}{2} + 6 \cdot \frac{1}{2} \\[0.8em] t &= -6 + 3 \\[0.8em] t &= -3 \end{align*}\]
\(\Longrightarrow \quad\)für \(t = -3\) gilt: \(\overrightarrow{a} = \dfrac{3}{2} \cdot \overrightarrow{b} + \dfrac{1}{2} \cdot \overrightarrow{s}\)
Für \(t = -3\) lässt sich der Vektor \(\overrightarrow{a}\) als Linearkombination der Vektoren \(\overrightarrow{b}\) und \(\overrightarrow{c}\) darstellen. Die drei Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) sind somit für \(t = -3\) linear abhängig und liegen in einer Ebene.

