Spezielle Vierecke
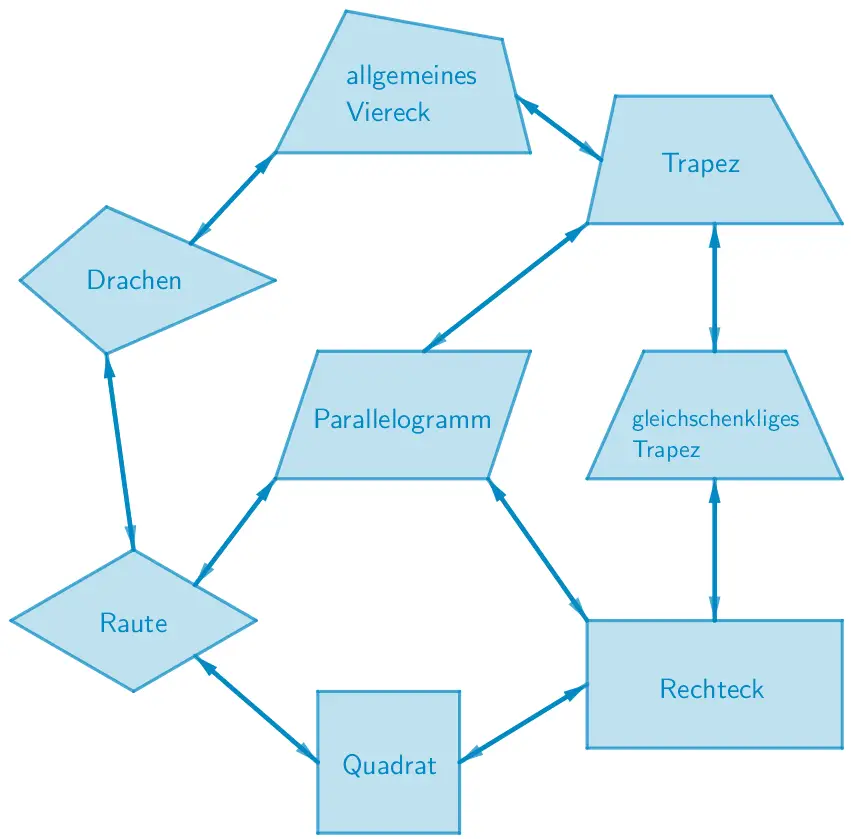
Die Abbildung zeigt ausgehend vom allgemeinen Viereck die zunehmende Spezialisierung der Vierecke.
So ist beispielsweise eine Raute ein spezielles Parallelogramm mit vier gleich langen Seiten und ein Quadrat ist eine spezielle Raute mit vier rechten Innenwinkeln.
Von unten nach oben betrachtet, bedeutet die Abbildung beispielsweise: Ein Quadrat ist auch ein Rechteck, ist auch ein Parallelogramm usw.
Nachweis spezieller Vierecke mit Vektoren
Die nachfolgenden Nachweise setzen voraus, dass vier bekannte Punkte ein Viereck festlegen, die Punkte also in einer Ebene liegen.
(Vorkenntnisse: Abiturskript - 2.1.1 Rechnen mit Vektoren, Abiturskript - 2.1.2 Lineare (Un-)Abhängigkeit von Vektoren und Abiturskript - 2.1.3 Skalarprodukt von Vektoren)
Trapez
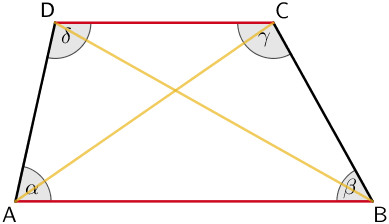
Eigenschaften
- Seiten: ein Paar parallele Seiten
- Winkel: vier unterschiedlich große Winkel
- Diagonalen: zwei Diagonalen
Nachweis
Zeigen, dass zwei der Verbindungsvektoren \(\overrightarrow{AB}\), \(\overrightarrow{DC}\), \(\overrightarrow{AD}\) und \(\overrightarrow{BC}\) zueinander parallel sind. Das ist dann der Fall, wenn die Vektoren ein Vielfaches voneinander sind.
Beispielsweise:
\[\textcolor{#cc071e}{\overrightarrow{AB}} = k \cdot \textcolor{#cc071e}{\overrightarrow{DC}}; \; k \in \mathbb R \; \Rightarrow \; \textcolor{#cc071e}{\overrightarrow{AB} \parallel \overrightarrow{DC}}\]
Drachen
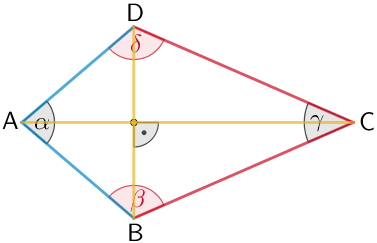
Eigenschaften
- Seiten: je zwei gleich lange anliegende Seiten
- Winkel: zwei gleich große gegenüberliegende Winkel
- Diagonalen: zueinander senkrechte Diagonalen
Nachweis
Entweder zeigen, dass je zwei anliegende Seiten gleich lang sind:
\(\textcolor{#0087c1}{\vert\overrightarrow{AB}\vert = \vert\overrightarrow{AD}\vert}\) und \(\textcolor{#cc071e}{\vert\overrightarrow{CB}\vert = \vert\overrightarrow{CD}\vert}\)
Oder zeigen, dass die Diagonalen zueinander senkrecht sind:
\[\textcolor{#e9b509}{\overrightarrow{AC} \circ \overrightarrow{BD} = 0 \; \Leftrightarrow \; \overrightarrow{AC} \perp \overrightarrow{BD}}\]
Parallelogramm
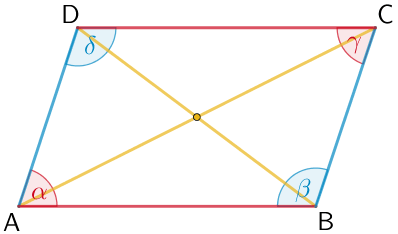
Eigenschaften
- Seiten: je zwei gleich lange parallele Seiten
- Winkel: gleich große gegenüberliegende Winkel
- Diagonalen: Diagonalen halbieren sich
Nachweis
Entweder zeigen, dass zwei gegenüberliegende Seiten parallel und gleich lang sind:
\(\textcolor{#cc071e}{\overrightarrow{AB} = \overrightarrow{DC}}\) oder \(\textcolor{#0087c1}{\overrightarrow{AD} = \overrightarrow{BC}}\)
Oder zeigen, dass die Mittelpunkte der Diagonalen identisch sind:
\[\begin{align*} \textcolor{#e9b509}{\overrightarrow{M}_{[AC]}}\; &\textcolor{#e9b509}{= \overrightarrow{M}_{[BD]}} \\[0.8em] \frac{1}{2}\cdot (\overrightarrow{A} + \overrightarrow{C}) &= \frac{1}{2} \cdot (\overrightarrow{B} + \overrightarrow{D}) &&| \cdot 2 \\[0.8em] \overrightarrow{A} + \overrightarrow{C} &= \overrightarrow{B} + \overrightarrow{D}\end{align*}\]
Raute
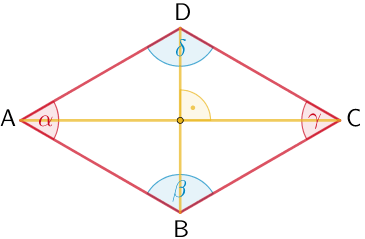
Eigenschaften
- Seiten: vier gleich lange Seiten
- Winkel: gleich große gegenüberliegende Winkel
- Diagonalen: zueinander senkrechte Diagonalen halbieren sich
Nachweis
Entweder zeigen, dass alle vier Seiten gleich lang sind:
\[\textcolor{#cc071e}{\vert\overrightarrow{AB}\vert = \vert\overrightarrow{BC}\vert = \vert\overrightarrow{CD}\vert = \vert\overrightarrow{DA}\vert}\]
Oder zeigen, dass die Mittelpunkte der Diagonalen identisch sind und die Diagonalen zueinander senkrecht sind:
\(\textcolor{#e9b509}{\overrightarrow{M}_{[AC]} = \overrightarrow{M}_{[BD]}}\) (vgl. Parallelogramm)
und
\[\textcolor{#e9b509}{\overrightarrow{AC} \circ \overrightarrow{BD} = 0 \; \Leftrightarrow \; \overrightarrow{AC} \perp \overrightarrow{BD}}\]
Rechteck
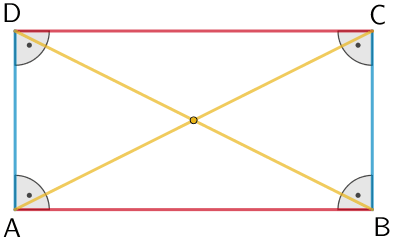
Eigenschaften
- Seiten: gleich lange gegenüberliegende Seiten
- Winkel: vier rechte Innenwinkel
- Diagonalen: gleich lange Diagonalen halbieren sich
Nachweis
Entweder zeigen, dass je zwei gegenüberliegende Seiten gleich lang sind und zwei anliegende Seiten einen rechten Winkel einschließen:
\(\textcolor{#cc071e}{\vert\overrightarrow{AB}\vert = \vert\overrightarrow{CD}\vert}\) und \(\textcolor{#0087c1}{\vert \overrightarrow{BC} \vert = \vert \overrightarrow{DA} \vert}\)
und (beispielsweise)
\[\textcolor{#cc071e}{\overrightarrow{AB}} \circ \textcolor{#0087c1}{\overrightarrow{AD}} = 0 \; \Leftrightarrow \; \textcolor{#cc071e}{\overrightarrow{AB}} \perp \textcolor{#0087c1}{\overrightarrow{AD}}\]
Oder zeigen, dass die Mittelpunkte der Diagonalen identisch sind und die Diagonalen gleich lang sind:
\(\textcolor{#e9b509}{\overrightarrow{M}_{[AC]} = \overrightarrow{M}_{[BD]}}\) (vgl. Parallelogramm)
und
\[\textcolor{#e9b509}{\vert \overrightarrow{AC} \vert = \vert \overrightarrow{BD}\vert}\]
Quadrat
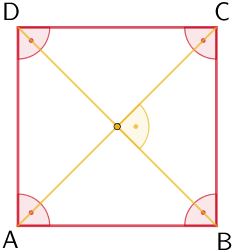
Eigenschaften
- Seiten: vier gleich lange Seiten
- Winkel: vier rechte Innenwinkel
- Diagonalen: zueinander senkrechte, gleich lange Diagonalen halbieren sich
Nachweis
Entweder zeigen, dass alle vier Seiten gleich lang sind und zwei anliegende Seiten einen rechten Winkel einschließen:
\[\textcolor{#cc071e}{\vert\overrightarrow{AB}\vert = \vert\overrightarrow{BC}\vert = \vert\overrightarrow{CD}\vert = \vert\overrightarrow{DA}\vert}\]
und (beispielsweise)
\[\textcolor{#cc071e}{\overrightarrow{AB} \circ \overrightarrow{AD} = 0 \; \Leftrightarrow \; \overrightarrow{AB} \perp \overrightarrow{AD}}\]
Oder zeigen, dass die Mittelpunkte der Diagonalen identisch sind und die Diagonalen zueinander senkrecht sind und die Diagonalen gleich lang sind:
\(\textcolor{#e9b509}{\overrightarrow{M}_{[AC]} = \overrightarrow{M}_{[BD]}}\) (vgl. Parallelogramm)
und
\[\textcolor{#e9b509}{\overrightarrow{AC} \circ \overrightarrow{BD} = 0 \; \Leftrightarrow \; \overrightarrow{AC} \perp \overrightarrow{BD}}\]
und
\[\textcolor{#e9b509}{\vert \overrightarrow{AC} \vert = \vert \overrightarrow{BD}\vert}\]
Beispielaufgabe
Die Punkte \(P(-3|1|1)\), \(Q(12|-11|-15)\), \(R(27|1|1)\) und \(S(12|13|17)\) sind Eckpunkte des Vierecks \(PQRS\).
Zeigen Sie , dass das Viereck \(PQRS\) eine Raute ist, aber kein Quadrat.
Bei ebenen geometrischen Figuren - wie einem Viereck - werden die Eckpunkte gegen den Uhrzeigersinn bezeichnet.
Eine mögliche Planskizze der Raute \(PQRS\) könnte wie folgt aussehen:
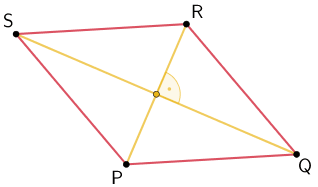
Planskizze der Raute \(PQRS\)
Nachweis der Raute \(PQRS\)
1. Möglichkeit: Zeigen, dass alle vier Seiten gleich lang sind
(vgl. Abiturskript - 2.1.1 Rechnen mit Vektoren, Betrag eines Vektors, Länge einer Strecke)
\(P(-3|1|1)\), \(Q(12|-11|-15)\), \(R(27|1|1)\), \(S(12|13|17)\)
\[\begin{align*} \textcolor{#cc071e}{\overline{PQ}} &= \vert \overrightarrow{PQ} \vert = \vert \overrightarrow{Q} - \overrightarrow{P} \vert \\[0.8em] &= \left| \begin{pmatrix} 12 \\ -11 \\ -15 \end{pmatrix} - \begin{pmatrix} -3 \\ 1 \\ 1 \end{pmatrix} \right| = \left| \begin{pmatrix} 15 \\ -12 \\ -16 \end{pmatrix} \right| \\[0.8em] &= \sqrt{15^{2} + (-12)^{2} + (-16)^{2}} = \sqrt{625} = \textcolor{#cc071e}{25} \end{align*}\]
\[\begin{align*} \textcolor{#cc071e}{\overline{QR}} &= \vert \overrightarrow{QR} \vert = \vert \overrightarrow{R} - \overrightarrow{Q} \vert \\[0.8em] &= \left| \begin{pmatrix} 27 \\ 1 \\ 1 \end{pmatrix} - \begin{pmatrix} 12 \\ -11 \\ -15 \end{pmatrix} \right| = \left| \begin{pmatrix} 15 \\ 12 \\ 16 \end{pmatrix} \right| \\[0.8em] &= \sqrt{15^{2} + 12^{2} + 16^{2}} = \sqrt{625} = \textcolor{#cc071e}{25} \end{align*}\]
\[\begin{align*} \textcolor{#cc071e}{\overline{RS}} &= \vert \overrightarrow{RS} \vert = \vert \overrightarrow{S} - \overrightarrow{R} \vert \\[0.8em] &= \left| \begin{pmatrix} 12 \\ 13 \\ 17 \end{pmatrix} - \begin{pmatrix} 27 \\ 1 \\ 1 \end{pmatrix} \right| = \left| \begin{pmatrix} -15 \\ 12 \\ 16 \end{pmatrix} \right| \\[0.8em] &= \sqrt{(-15)^{2} + 12^{2} + 16^{2}} = \sqrt{625} = \textcolor{#cc071e}{25} \end{align*}\]
\[\begin{align*} \textcolor{#cc071e}{\overline{SP}} &= \vert \overrightarrow{SP} \vert = \vert \overrightarrow{P} - \overrightarrow{S} \vert \\[0.8em] &= \left| \begin{pmatrix} -3 \\ 1 \\ 1 \end{pmatrix} - \begin{pmatrix} 12 \\ 13 \\ 17 \end{pmatrix} \right| = \left| \begin{pmatrix} -15 \\ -12 \\ -16 \end{pmatrix} \right| \\[0.8em] &= \sqrt{(-15)^{2} + (-12)^{2} + (-16)^{2}} = \sqrt{625} = \textcolor{#cc071e}{25} \end{align*}\]
\[\Rightarrow \enspace \textcolor{#cc071e}{\overline{PQ} = \overline{QR} = \overline{RS} = \overline{SP}}\]
Also ist das Viereck \(PQRS\) eine Raute.
2. Möglichkeit: Zeigen, dass die Diagonalen sich halbieren und zueinander senkrecht sind
(vgl. Abiturskript - 2.1.1 Rechnen mit Vektoren, Mittelpunkt einer Strecke, Abiturskript - 2.1.3 Skalarprodukt von Vektoren, Orthogonale Vektoren)

\(P(-3|1|1)\), \(Q(12|-11|-15)\), \(R(27|1|1)\), \(S(12|13|17)\)
\[\begin{align*} \textcolor{#e9b509}{M_{[SQ]}} &\textcolor{#e9b509}{=} \textcolor{#e9b509}{M_{[PR]}} \\[0.8em] \frac{1}{2} \cdot (\overrightarrow{S} + \overrightarrow{Q}) &= \frac{1}{2} \cdot (\overrightarrow{P} + \overrightarrow{R}) &&| \cdot 2 \\[0.8em] \overrightarrow{S} + \overrightarrow{Q} &= \overrightarrow{P} + \overrightarrow{R} \\[0.8em] \begin{pmatrix} 12 \\ 13 \\ 17 \end{pmatrix} + \begin{pmatrix} 12 \\ -11 \\ -15 \end{pmatrix} &= \begin{pmatrix} -3 \\ 1 \\ 1 \end{pmatrix} + \begin{pmatrix} 27 \\ 1 \\ 1 \end{pmatrix} \\[0.8em] \textcolor{#e9b509}{\begin{pmatrix} 24 \\ 2 \\ 2 \end{pmatrix}} &\textcolor{#e9b509}{\;= \begin{pmatrix} 24 \\ 2 \\ 2 \end{pmatrix}} \quad (\textcolor{#89ba17}{\text{w}})\end{align*}\]
Die Diagonalen \(\textcolor{#e9b509}{[SQ]}\) und \(\textcolor{#e9b509}{[PR]}\) halbieren sich.
\[\textcolor{#e9b509}{\overrightarrow{SQ}} = \overrightarrow{Q} - \overrightarrow{S} = \begin{pmatrix} 12 \\ -11 \\ -15 \end{pmatrix} - \begin{pmatrix} 12 \\ 13 \\ 17 \end{pmatrix} = \begin{pmatrix} 0 \\ -24 \\ -32 \end{pmatrix}\]
\[\textcolor{#e9b509}{\overrightarrow{PR}} = \overrightarrow{R} - \overrightarrow{P} = \begin{pmatrix} 27 \\ 1 \\ 1 \end{pmatrix} - \begin{pmatrix} -3 \\ 1 \\ 1 \end{pmatrix} = \begin{pmatrix} 30 \\ 0 \\ 0 \end{pmatrix}\]
\[\begin{align*} \textcolor{#e9b509}{\overrightarrow{SQ} \circ \overrightarrow{PR}} &= \begin{pmatrix} 0 \\ -24 \\ -32 \end{pmatrix} \circ \begin{pmatrix} 30 \\ 0 \\ 0 \end{pmatrix} \\[0.8em] &= 0 \cdot 30 + (-24) \cdot 0 + (-32) \cdot 0 \\[0.8em] &\textcolor{#e9b509}{\;= 0}\end{align*}\]
\[\Rightarrow \enspace \textcolor{#e9b509}{\overrightarrow{SQ} \perp \overrightarrow{PR}}\]
Somit ist das Viereck \(PQRS\) eine Raute.
Nachweis, dass die Raute \(PQRS\) kein Quadrat ist
Es ist zu zeigen, dass einer der Innenwinkel ungleich 90° ist, beispielsweise der Innenwinkel bei Punkt \(Q\).
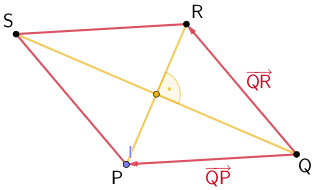
\(P(-3|1|1)\), \(Q(12|-11|-15)\), \(R(27|1|1)\)
\[\textcolor{#cc071e}{\overrightarrow{QP}} = \overrightarrow{P} - \overrightarrow{Q} = \begin{pmatrix} -3 \\ 1 \\ 1 \end{pmatrix} - \begin{pmatrix} 12 \\ -11 \\ -15 \end{pmatrix} = \begin{pmatrix} -15 \\ 12 \\ 16 \end{pmatrix}\]
\[\textcolor{#cc071e}{\overrightarrow{QR}} = \overrightarrow{R} - \overrightarrow{Q} = \begin{pmatrix} 27 \\ 1 \\ 1 \end{pmatrix} - \begin{pmatrix} 12 \\ -11 \\ -15 \end{pmatrix} = \begin{pmatrix} 15 \\ 12 \\ 16 \end{pmatrix}\]
\[\begin{align*} \textcolor{#cc071e}{\overrightarrow{QP} \circ \overrightarrow{QR}} &= \begin{pmatrix} -15 \\ 12 \\ 16 \end{pmatrix} \circ \begin{pmatrix} 15 \\ 12 \\ 16 \end{pmatrix} \\[0.8em] &= (-15) \cdot 15 + 12 \cdot 12 + 16 \cdot 16 \\[0.8em] &= 175 \\[0.8em] &\textcolor{#cc071e}{\;\neq 0}\end{align*}\]
\[\Rightarrow \enspace \textcolor{#cc071e}{\overrightarrow{QP} \cancel{\perp} \overrightarrow{QR}}\]
Also ist die Raute \(PQRS\) kein Quadrat.

