Gleichung einer Ebene in Parameterform (vgl. Merkhilfe)
Jede Ebene \(E\) kann durch eine Gleichung in der sogenannten Parameterform
\(E \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u} + \mu \cdot \overrightarrow{v} \enspace\) mit den Parametern \(\lambda, \mu \in \mathbb R\) beschrieben werden.
Dabei ist \(\overrightarrow{A}\) der Ortsvektor eines Aufpunkts (Stützvektor) der Ebene. \(\overrightarrow{u}\) und \(\overrightarrow{v}\) sind zwei linear unabhängige Richtungsvektoren (Spannvektoren).
Eine Ebene wird durch folgende Angaben eindeutig festgelegt:
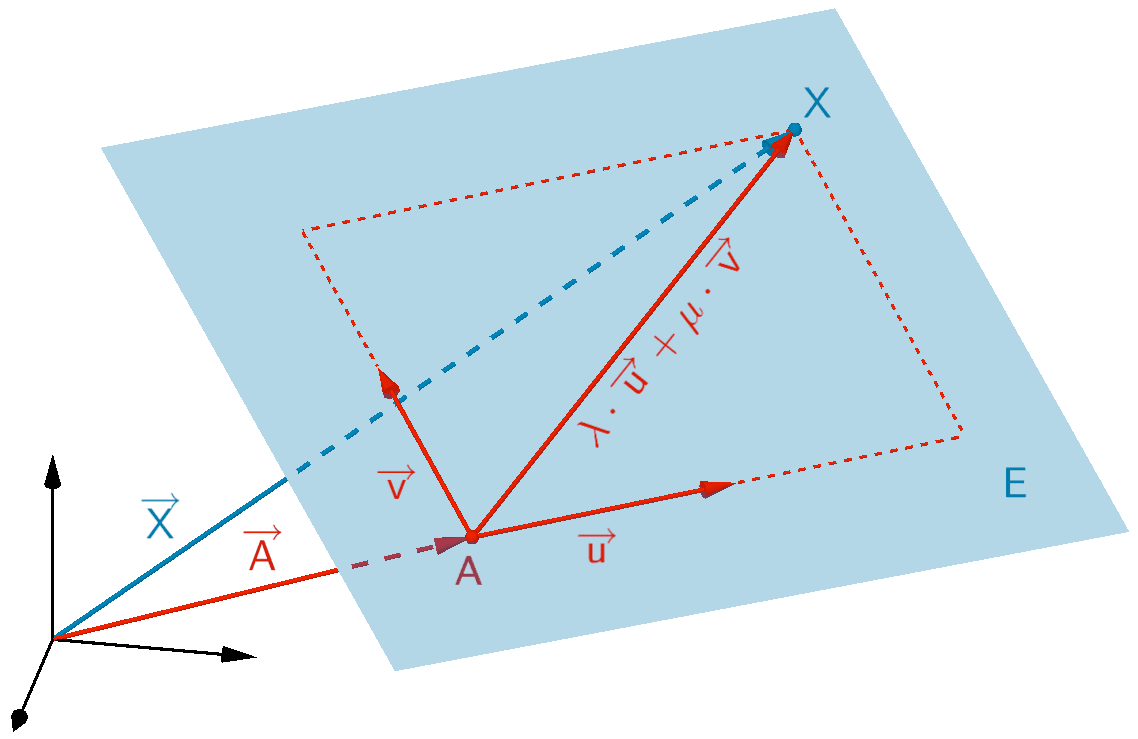
Ein Punkt \(A\) und zwei linear unabhängige Vektoren \(\overrightarrow{u}\) und \(\overrightarrow{v}\)
\[E \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u} + \mu \cdot \overrightarrow{v}; \; \lambda, \mu \in \mathbb R\]
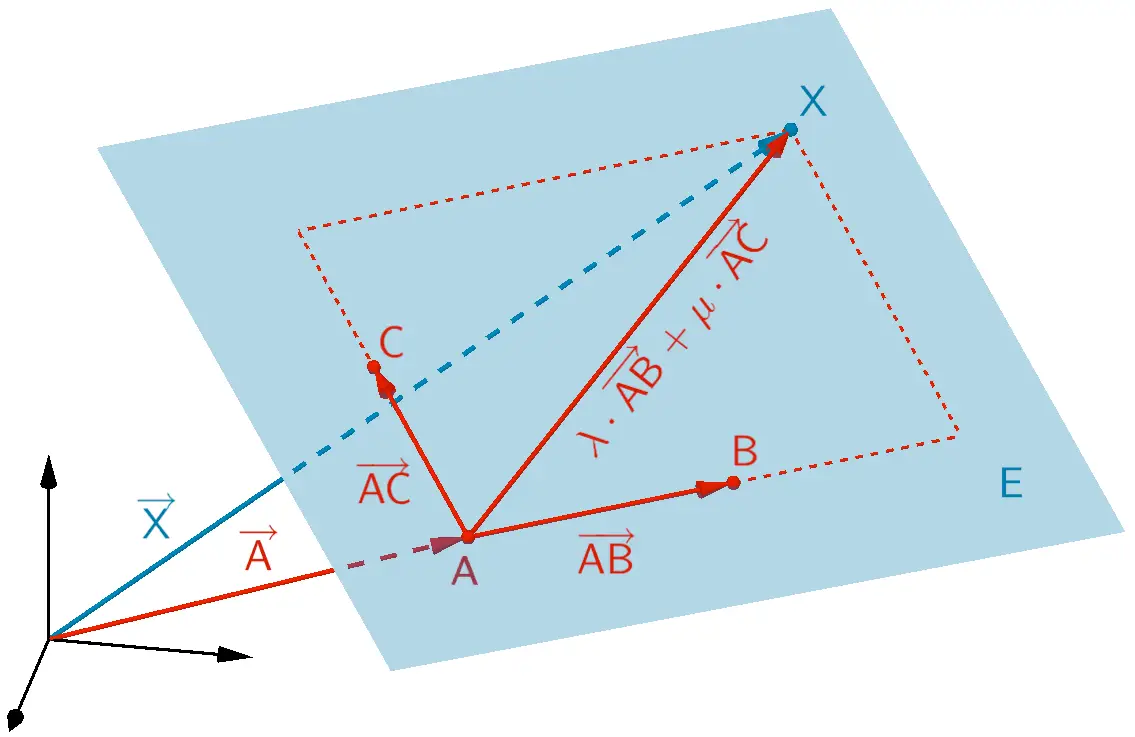
Drei Punkte \(A\), \(B\) und \(C\), die nicht auf einer Geraden liegen
\[E \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{AB} + \mu \cdot \overrightarrow{AC}; \; \lambda, \mu \in \mathbb R\]
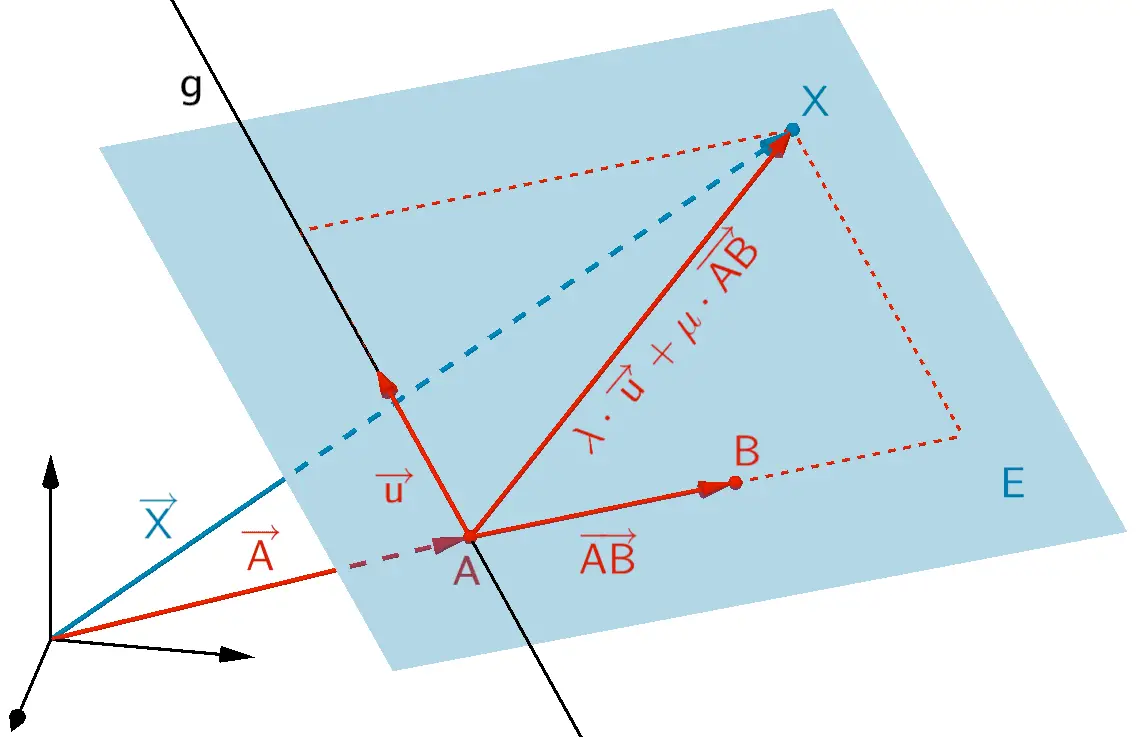
Eine Gerade \(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}\) und einen Punkt \(B \notin g\)
\[E \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u} + \mu \cdot \overrightarrow{AB}; \; \lambda, \mu \in \mathbb R\]
Zwei sich schneidende Geraden \(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}\) und \(h \colon \overrightarrow{X} = \overrightarrow{B} + \mu \cdot \overrightarrow{v}\)
\[E \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u} + \mu \cdot \overrightarrow{v}; \; \lambda, \mu \in \mathbb R\]
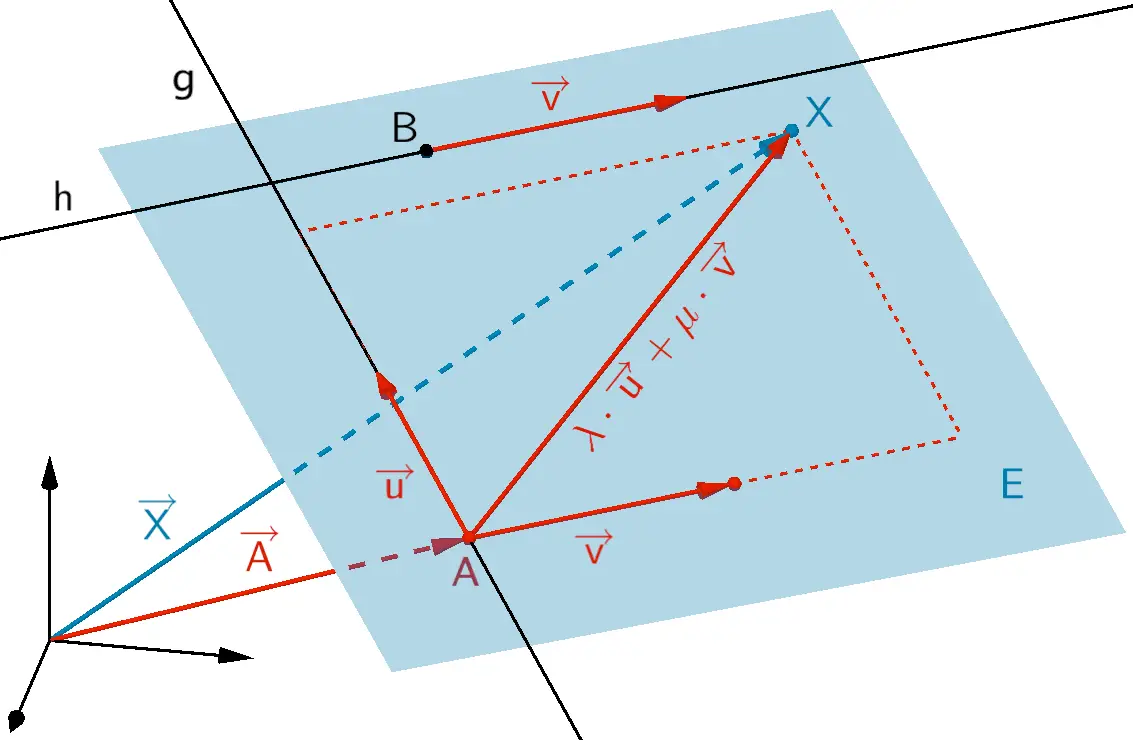
Zwei parallele Geraden \(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}\) und \(h \colon \overrightarrow{X} = \overrightarrow{B} + \mu \cdot \overrightarrow{v}\)
\[E \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u} + \mu \cdot \overrightarrow{AB}; \; \lambda, \mu \in \mathbb R\]
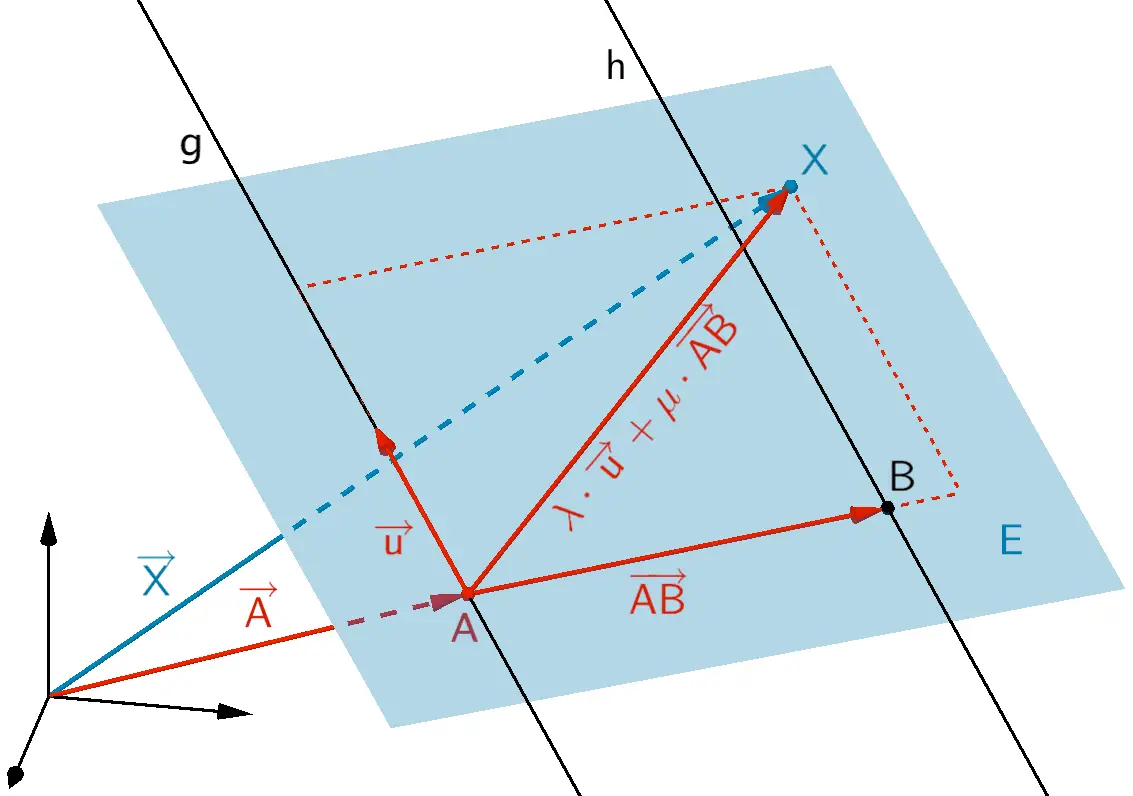
Zu jedem Wert der Parameter \(\lambda\) und \(\mu\) gehört genau ein Punkt \(X\) in der Ebene \(E\). Als Aufpunkt \(A\) kann jeder Punkt der Ebene \(E\) gewählt werden. Als Richtungsvektoren der Ebene \(E\) kommt jedes beliebige Vielfache der Vektoren \(\overrightarrow{u}\), \(\overrightarrow{v}\) bzw. \(\overrightarrow{AB}\) in Frage. Die Gleichung einer Ebene in Parameterform ist also nicht eindeutig bestimmt.
Spurgeraden einer Ebene (Ebenengleichung in Parameterform)
Spurgeraden sind die Schnittgeraden einer Ebene mit den Koordinatenebenen. Anhand der Spurgeraden lässt sich die Lage einer Ebene im Koordinatensystem veranschaulichen.
Anmerkung: An dieser Stelle sei darauf verwiesen, dass die Bestimmung der Spurgeraden einer Ebene einfacher ist, wenn die Gleichung der Ebene in der Normalenorm in Koordinatendarstellung vorliegt (vgl. Abiturskript - 2.2.3 Ebenengleichung in Normalenform).
Bestimmung der Spurgeraden einer Ebene
Man bestimmt zunächst die Schnittpunkte einer Ebene mit den Koordinatenachsen (Spurpunkte). Anschließend formuliert man mithilfe dieser Schnittpunkte die Gleichungen der Spurgeraden. Zwei Koordinaten eines Schnittpunkts einer Ebene mit einer Koordinatenachse sind gleich Null. Sonderfall: Eine Ebene verläuft durch den Ursprung.
Schnittpunkt einer Ebene mit der \(x_{1}\)-Achse: \(S_{x_{1}}(s_{1}|0|0)\)
Schnittpunkt einer Ebene mit der \(x_{2}\)-Achse: \(S_{x_{2}}(0|s_{2}|0)\)
Schnittpunkt einer Ebene mit der \(x_{3}\)-Achse: \(S_{x_{3}}(0|0|s_{3})\)
Liegt eine Ebene \(E\) in der Parameterform \(E \colon \overrightarrow{X} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} + \lambda \cdot \begin{pmatrix} u_{1} \\ u_{2} \\ u_{3} \end{pmatrix} + \mu \cdot \begin{pmatrix} v_{1} \\ v_{2} \\ v_{3} \end{pmatrix}; \; \lambda, \mu \in \mathbb R\) vor, ergibt sich für die Berechnung eines Schnittpunkts der Ebene \(E\) mit einer der Koordinatenachsen jeweils ein Gleichungssystem zur Bestimmung der Parameter \(\lambda\) und \(\mu\).
Gleichungssystem zur Berechnung des Schnittpunkts der Ebene \(E\) mit der \(x_{1}\)-Achse:
\[\begin{align*} \text{I} & & & a_{2} + \lambda \cdot u_{2} + \mu \cdot v_{2} = 0 \\[0.8em] \text{II} & & \wedge \enspace & a_{3} + \lambda \cdot u_{3} + \mu \cdot v_{3} = 0 \end{align*}\]
Gleichungssystem zur Berechnung des Schnittpunkts der Ebene \(E\) mit der \(x_{2}\)-Achse:
\[\begin{align*} \text{I} & & & a_{1} + \lambda \cdot u_{1} + \mu \cdot v_{1} = 0 \\[0.8em] \text{II} & & \wedge \enspace & a_{3} + \lambda \cdot u_{3} + \mu \cdot v_{3} = 0 \end{align*}\]
Gleichungssystem zur Berechnung des Schnittpunkts der Ebene \(E\) mit der \(x_{3}\)-Achse:
\[\begin{align*} \text{I} & & & a_{1} + \lambda \cdot u_{1} + \mu \cdot v_{1} = 0 \\[0.8em] \text{II} & & \wedge \enspace & a_{2} + \lambda \cdot u_{2} + \mu \cdot v_{2} = 0 \end{align*}\]
Existiert ein Schnittpunkt mit einer Koordinatenachse, liefert das jeweilige Gleichungssystem je einen Wert für die Parameter \(\lambda\) und \(\mu\). Diese setzt man in die Gleichung der Ebene \(E\) in Parameterform ein und erhält den Ortsvektor des jeweiligen Schnittpunkts der Ebene \(E\) mit der Koordinatenachse (Spurpunkt).
Beispiel:
Gegeben sei die Ebene \(E \colon \overrightarrow{X} = \begin{pmatrix} -5 \\ 6 \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -5 \\ 3 \\ 1 \end{pmatrix} + \mu \cdot \begin{pmatrix} 5 \\ -6 \\ 2 \end{pmatrix}; \; \lambda, \mu \in \mathbb R\).
Ermitteln Sie die Gleichungen der Spurgeraden der Ebene \(E\).
Um die Gleichung der Spurgeraden aufstellen zu können, werden zunächst die Schnittpunkte \(S_{x_{1}}\), \(S_{x_{2}}\) und \(S_{x_{3}}\) der Ebene \(E\) mit den Koordinatenachsen (Spurpunkte) bestimmt.
Schnittpunkt \(S_{x_{1}}\) der Ebene \(E\) mit der \(x_{1}\)-Achse
\[E \colon \overrightarrow{X} = \begin{pmatrix} -5 \\ 6 \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -5 \\ 3 \\ 1 \end{pmatrix} + \mu \cdot \begin{pmatrix} 5 \\ -6 \\ 2 \end{pmatrix}\]
\[S_{x_{1}}(s_{1}|0|0)\]
Es ergibt sich folgendes Gleichungssystem:
\[\begin{align*} \text{I} & & & 6 + 3\lambda - 6\mu = 0 \\[0.8em] \text{II}& & \wedge \enspace &2 + \enspace \lambda + 2 \mu = 0 \end{align*}\]
Das Gleichungssystem lässt sich beispielsweise mit dem Additionsverfahren lösen.
\[\begin{align*}3 \cdot \text{II} - \text{I}\colon \; 3 \cdot 2 - 6 + 3 \cdot \lambda - 3\lambda + 3 \cdot 2\mu - (-6\mu) &= 0 \\[0.8em] 12\mu &= 0 \\[0.8em] \mu &= 0 \end{align*}\]
\[\begin{align*} \mu = 0 \; \text{in II}\colon \; 2 + \lambda + 2 \cdot 0 &= 0 \\[0.8em] 2 + \lambda &= 0 & &| - 2 \\[0.8em] \lambda &= -2 \end{align*}\]
Parameterwerte \(\lambda = -2\) und \(\mu = 0\) in die Gleichung der Ebene \(E\) einsetzen:
\[\overrightarrow{S}_{x_{1}} = \begin{pmatrix} -5 \\ 6 \\ 2 \end{pmatrix} - 2 \cdot \begin{pmatrix} -5 \\ 3 \\ 1 \end{pmatrix} + 0 \cdot \begin{pmatrix} 5 \\ -6 \\ 2 \end{pmatrix} = \begin{pmatrix} 5 \\ 0 \\ 0 \end{pmatrix}\]
\[\Longrightarrow \quad S_{x_{1}}(5|0|0)\]
Schnittpunkt \(S_{x_{2}}\) der Ebene \(E\) mit der \(x_{2}\)-Achse
\[E \colon \overrightarrow{X} = \begin{pmatrix} -5 \\ 6 \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -5 \\ 3 \\ 1 \end{pmatrix} + \mu \cdot \begin{pmatrix} 5 \\ -6 \\ 2 \end{pmatrix}\]
\[S_{x_{2}}(0|s_{2}|0)\]
Es ergibt sich folgendes Gleichungssystem:
\[\begin{align*} \text{I} & & & -5 - 5\lambda + 5\mu = 0 \\[0.8em] \text{II}& & \wedge & \quad \; 2 + \enspace \lambda + 2 \mu = 0 \end{align*}\]
Das Gleichungssystem lässt sich beispielsweise mit dem Additionsverfahren lösen.
\[\begin{align*}5 \cdot \text{II} + \text{I}\colon \; 5 \cdot 2 - 5 + 5 \cdot \lambda - 5\lambda + 5 \cdot 2\mu + 5\mu &= 0 \\[0.8em] 5 + 15\mu &= 0 & &| - 5 \\[0.8em] 15\mu &= -5 & &| : 15 \\[0.8em] \mu &= -\frac{1}{3} \end{align*}\]
\[\begin{align*} \mu = -\frac{1}{3} \; \text{in II}\colon \; 2 + \lambda + 2 \cdot -\frac{1}{3} &= 0 \\[0.8em] \frac{4}{3} + \lambda &= 0 & &| - \frac{4}{3} \\[0.8em] \lambda &= -\frac{4}{3} \end{align*}\]
Parameterwerte \(\lambda = -\dfrac{4}{3}\) und \(\mu = -\dfrac{1}{3}\) in die Gleichung der Ebene \(E\) einsetzen:
\[\begin{align*} \overrightarrow{S}_{x_{2}} &= \begin{pmatrix} -5 \\ 6 \\ 2 \end{pmatrix} - \frac{4}{3} \cdot \begin{pmatrix} -5 \\ 3 \\ 1 \end{pmatrix} - \frac{1}{3} \cdot \begin{pmatrix} 5 \\ -6 \\ 2 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} -5 \\ 6 \\ 2 \end{pmatrix} + \begin{pmatrix} \frac{20}{3} \\ -4 \\ -\frac{4}{3} \end{pmatrix} + \begin{pmatrix} -\frac{5}{3} \\ 2 \\ -\frac{2}{3} \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 0 \\ 4 \\ 0 \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad S_{x_{2}}(0|4|0)\]
Schnittpunkt \(S_{x_{3}}\) der Ebene \(E\) mit der \(x_{3}\)-Achse
\[E \colon \overrightarrow{X} = \begin{pmatrix} -5 \\ 6 \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -5 \\ 3 \\ 1 \end{pmatrix} + \mu \cdot \begin{pmatrix} 5 \\ -6 \\ 2 \end{pmatrix}\]
\[S_{x_{3}}(0|0|s_{3})\]
Es ergibt sich folgendes Gleichungssystem:
\[\begin{align*} \text{I} & & & -5 - 5\lambda + 5\mu = 0 \\[0.8em] \text{II}& & \wedge & \quad \;6 + 3\lambda - 6 \mu = 0 \end{align*}\]
Das Gleichungssystem lässt sich beispielsweise mit dem Additionsverfahren lösen.
\[\begin{align*}3 \cdot \text{I} + 5 \cdot \text{II}\colon \; 3 \cdot (-5) + 5 \cdot 6 + 3 \cdot (-5\lambda) + 5 \cdot 3\lambda + 3 \cdot 5\mu + 5 \cdot (-6\mu) &= 0 \\[0.8em] -15 + 30 - 15\lambda + 15\lambda + 15\mu - 30\mu &= 0 \\[0.8em] 15 - 15\mu &= 0 & &| + 15\mu \\[0.8em] 15 &= 15\mu & &| : 15 \\[0.8em] 1 &= \mu \end{align*}\]
\[\begin{align*} \mu = 1 \; \text{in II}\colon \; 6 + 3\lambda - 6 \cdot 1 &= 0 \\[0.8em] 3\lambda &= 0 \\[0.8em] \lambda &= 0 \end{align*}\]
Parameterwerte \(\lambda = 0\) und \(\mu = 1\) in die Gleichung der Ebene \(E\) einsetzen:
\[\overrightarrow{S}_{x_{3}} = \begin{pmatrix} -5 \\ 6 \\ 2 \end{pmatrix} + 0 \cdot \begin{pmatrix} -5 \\ 3 \\ 1 \end{pmatrix} + 1 \cdot \begin{pmatrix} 5 \\ -6 \\ 2 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 4 \end{pmatrix}\]
\[\Longrightarrow \quad S_{x_{3}}(0|0|4)\]
Gleichungen der Spurgeraden
Jeweils zwei Schnittpunkte der Ebene \(E\) mit einer Koordinatenachse (Spukpunkte) legen eine Spurgerade fest. Als Aufpunkt für die Geradengleichung einer Spurgeraden lkann einer der Schnittpunkte gewählt werden. Als Richtungsvektor eignet sich der Verbindungsvektor zweier Schnittpunkte (vgl. Abiturskript - 2.2.1 Geradengleichung in Parameterform).
Spurgerade der Ebene \(E\) in der \(x_{1}x_{2}\)-Ebene
\(S_{x_{1}}(5|0|0)\), \(S_{x_{2}}(0|4|0)\)
\[S_{x_{1}}S_{x_{2}} \colon \overrightarrow{X} = \overrightarrow{S}_{x_{1}} + \lambda \cdot \overrightarrow{S_{x_{1}}S_{x_{2}}}; \; \lambda \in \mathbb R\]
\[\overrightarrow{S_{x_{1}}S_{x_{2}}} = \overrightarrow{S}_{x_{2}} - \overrightarrow{S}_{x_{1}} = \begin{pmatrix} 0 \\ 4 \\ 0 \end{pmatrix} - \begin{pmatrix} 5 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} -5 \\ 4 \\ 0 \end{pmatrix}\]
\[\Longrightarrow \quad S_{x_{1}}S_{x_{2}} \colon \overrightarrow{X} = \begin{pmatrix} 5 \\ 0 \\ 0 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -5 \\ 4 \\ 0 \end{pmatrix}; \; \lambda \in \mathbb R\]
Spurgerade der Ebene \(E\) in der \(x_{1}x_{3}\)-Ebene
\(S_{x_{1}}(5|0|0)\), \(S_{x_{3}}(0|0|4)\)
\[S_{x_{1}}S_{x_{3}} \colon \overrightarrow{X} = \overrightarrow{S}_{x_{1}} + \mu \cdot \overrightarrow{S_{x_{1}}S_{x_{3}}}\,; \enspace \mu \in \mathbb R\]
\[\overrightarrow{S_{x_{1}}S_{x_{3}}} = \overrightarrow{S}_{x_{3}} - \overrightarrow{S}_{x_{1}} = \begin{pmatrix} 0 \\ 0 \\ 4 \end{pmatrix} - \begin{pmatrix} 5 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} -5 \\ 0 \\ 4 \end{pmatrix}\]
\[\Longrightarrow \quad S_{x_{1}}S_{x_{3}} \colon \overrightarrow{X} = \begin{pmatrix} 5 \\ 0 \\ 0 \end{pmatrix} + \mu \cdot \begin{pmatrix} -5 \\ 0 \\ 4 \end{pmatrix}; \; \mu \in \mathbb R\]
Spurgerade der Ebene \(E\) in der \(x_{2}x_{3}\)-Ebene
\[S_{x_{2}}(0|4|0)\,, \enspace S_{x_{3}}(0|0|4)\]
\[S_{x_{2}}S_{x_{3}} \colon \overrightarrow{X} = \overrightarrow{S}_{x_{2}} + \tau \cdot \overrightarrow{S_{x_{2}}S_{x_{3}}}\,; \enspace \tau \in \mathbb R\]
\[\overrightarrow{S_{x_{2}}S_{x_{3}}} = \overrightarrow{S}_{x_{3}} - \overrightarrow{S}_{x_{2}} = \begin{pmatrix} 0 \\ 0 \\ 4 \end{pmatrix} - \begin{pmatrix} 0 \\ 4 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ -4 \\ 4 \end{pmatrix} = 4 \cdot \begin{pmatrix} 0 \\ -1 \\ 1 \end{pmatrix}\]
\[\Longrightarrow \quad S_{x_{2}}S_{x_{3}} \colon \overrightarrow{X} = \begin{pmatrix} 0 \\ 4 \\ 0 \end{pmatrix} + \tau \cdot \begin{pmatrix} 0 \\ -1 \\ 1 \end{pmatrix}; \; \tau \in \mathbb R\]
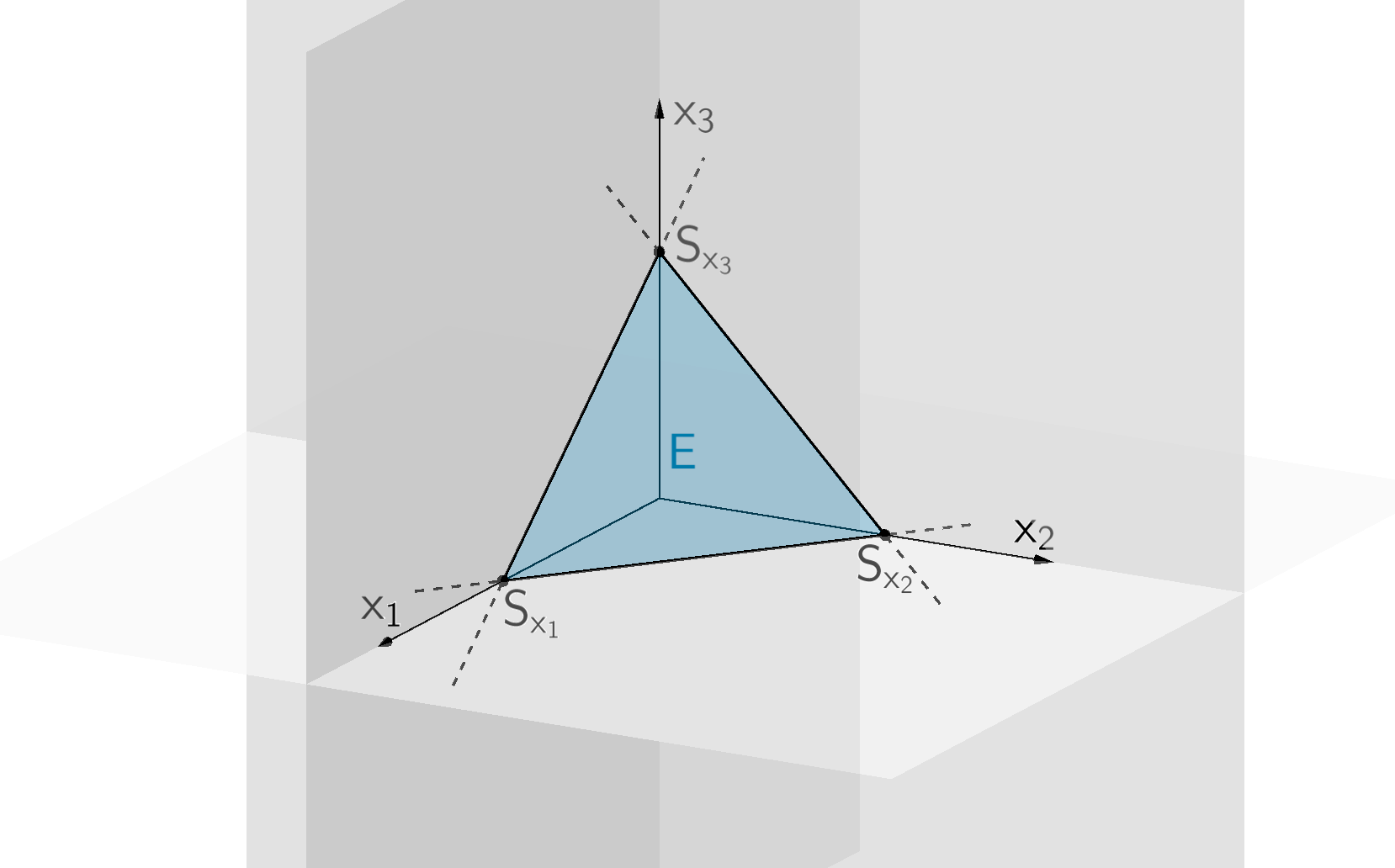
Schnittpunkte \(S_{x_{1}}\), \(S_{x_{2}}\) und \(S_{x_{3}}\) der Ebene \(E\) mit den Koordinatenachsen sowie Spurgeraden \(S_{x_{1}}S_{x_{2}}\), \(S_{x_{1}}S_{x_{3}}\) und \(S_{x_{2}}S_{x_{3}}\) der Ebene \(E\) mit den Koordinatenebenen. Das Dreieck \(S_{x_{1}}S_{x_{2}}S_{x_{3}}\) repräsentiert die Ebene \(E\).
Beispielaufgabe
Gegeben seien die Punkte \(A(6|2|1)\), \(B(-3|4|5)\), \(C(5|5|-2)\) und \(D(-4|7|2)\). Die parallelen Geraden \(AB\) und \(CD\) legen die Ebene \(E\) fest.
Weisen Sie die Parallelität der Geraden \(AB\) und \(CD\) nach und bestimmen Sie eine Gleichung der Ebene \(E\) in Parameterform.
Nachweis der Parallelität der Geraden \(AB\) und \(CD\)
Die Geraden \(AB\) und \(CD\) sind zueinander parallel, wenn deren Richtungsvektoren linear abhängig sind (vgl. Abiturskript - 2.1.2 Lineare (Un-)Abhängigkeit von Vektoren). Richtungsvektoren der Geraden \(AB\) und \(CD\) sind beispielweise die Verbindungsvektoren \(\overrightarrow{AB}\) und \(\overrightarrow{CD}\).
\(A(6|2|1)\), \(B(-3|4|5)\), \(C(5|5|-2)\), \(D(-4|7|2)\)
\[\overrightarrow{AB} = \overrightarrow{B} - \overrightarrow{A} = \begin{pmatrix} -3 \\ 4 \\ 5 \end{pmatrix} - \begin{pmatrix} 6 \\ 2 \\ 1 \end{pmatrix} = \begin{pmatrix} -9 \\ 2 \\ 4 \end{pmatrix}\]
\[\overrightarrow{CD} = \overrightarrow{D} - \overrightarrow{C} = \begin{pmatrix} -4 \\ 7 \\ 2 \end{pmatrix} - \begin{pmatrix} 5 \\ 5 \\ -2 \end{pmatrix} = \begin{pmatrix} -9 \\ 2 \\ 4 \end{pmatrix}\]
\[\Longrightarrow \quad \overrightarrow{AB} = \overrightarrow{CD} \quad \Longrightarrow \quad AB \parallel CD\]
Gleichung der Ebene \(E\) in Parameterform
Um die Gleichung der Ebene \(E\) in Parameterfom aufstellen zu können, benötigt man eine Aufpunkt und zwei linear unabhängige Richtungsvektoren.
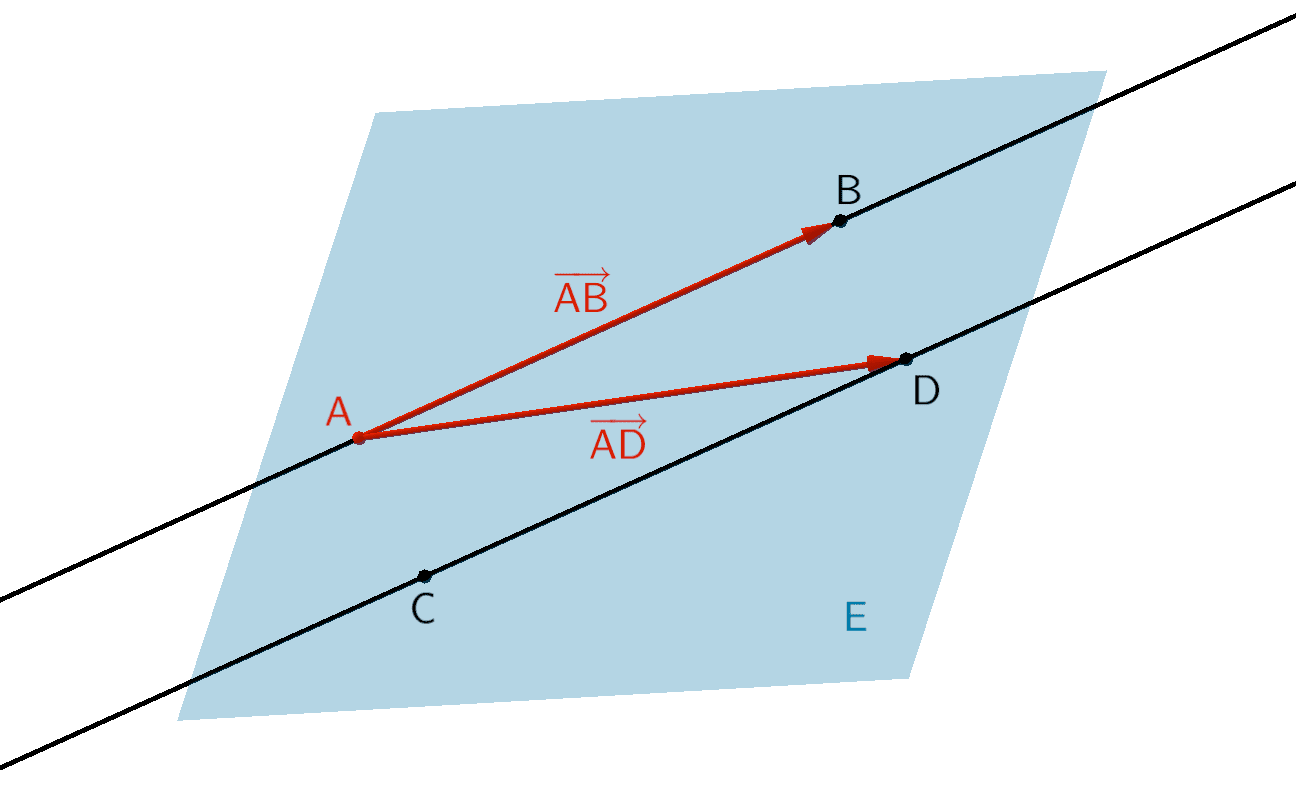
Beispielweise wählt man als Aufpunkt den Punkt \(A\) und als linear unabhängige Richtungsvektoren die Verbindungsvektoren \(\overrightarrow{AB}\) und \(\overrightarrow{AD}\) (ggf. ein Vielfaches der Verbindungsvektoren).
\[E \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{AB} + \mu \cdot \overrightarrow{AD}; \; \lambda, \mu \in \mathbb R\]
Verbindungsvektor \(\overrightarrow{AD}\) berechnen:
\(A(6|2|1)\), \(D(-4|7|2)\)
\[\overrightarrow{AD} = \overrightarrow{D} - \overrightarrow{A} = \begin{pmatrix} -4 \\ 7 \\ 2 \end{pmatrix} - \begin{pmatrix} 6 \\ 2 \\ 1 \end{pmatrix} = \begin{pmatrix} -10 \\ 5 \\ 1 \end{pmatrix}\]
Gleichung der Ebene \(E\) in Parameterform aufstellen:
\(A(6|2|1)\), \(\overrightarrow{AB} = \begin{pmatrix} -9 \\ 2 \\ 4 \end{pmatrix}\), \(\overrightarrow{AD} = \begin{pmatrix} -10 \\ 5 \\ 1 \end{pmatrix}\)
\[E \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{AB} + \mu \cdot \overrightarrow{AD}\,; \; \lambda, \mu \in \mathbb R\]
\[E \colon \overrightarrow{X} = \begin{pmatrix} 6 \\ 2 \\ 1 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -9 \\ 2 \\ 4 \end{pmatrix} + \mu \cdot \begin{pmatrix} -10 \\ 5 \\ 1 \end{pmatrix}; \; \lambda, \mu \in \mathbb R\]

