Lagebeziehung zwischen Gerade und Ebene
Bei der gegenseitigen Lage zwischen einer Gerade \(g\) und einer Ebene \(E\) lassen sich drei Fälle unterscheiden:
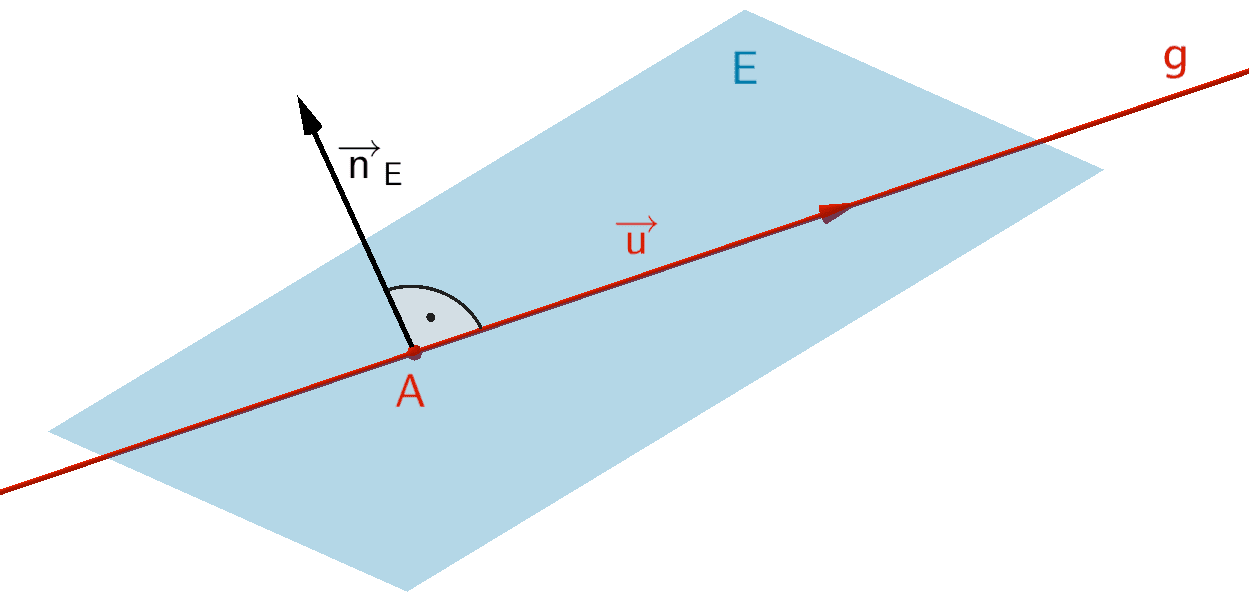
Die Gerade \(g\) liegt in der Ebene \(E\).
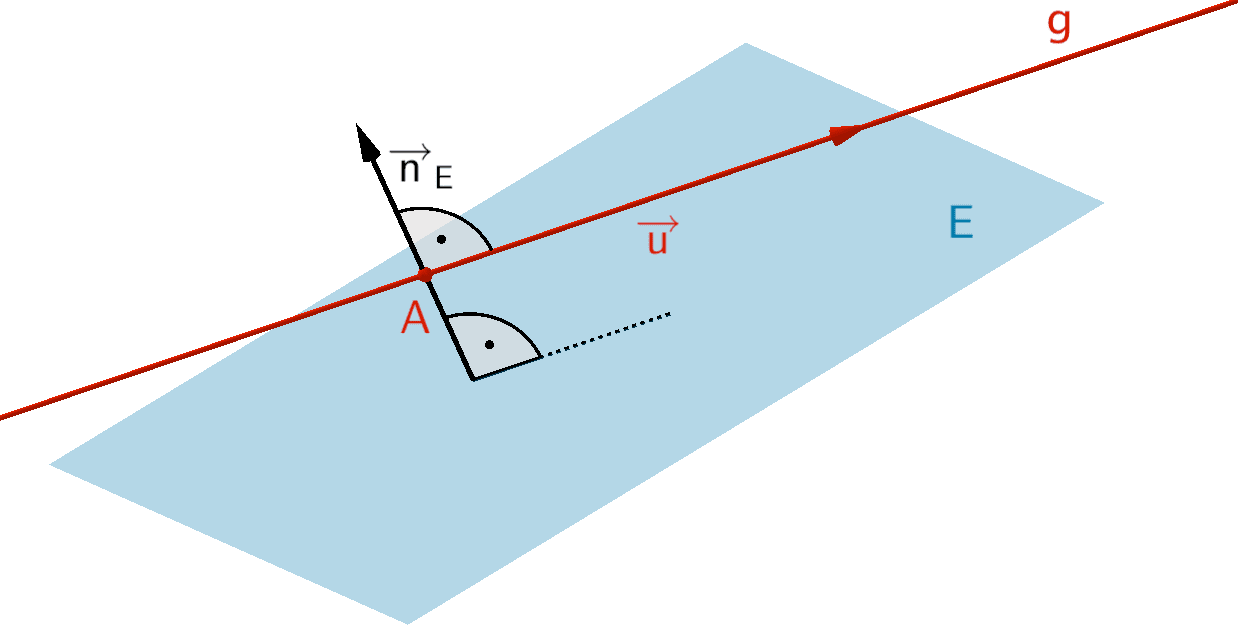
Die Gerade \(g\) verläuft (echt) parallel zur Ebene \(E\).
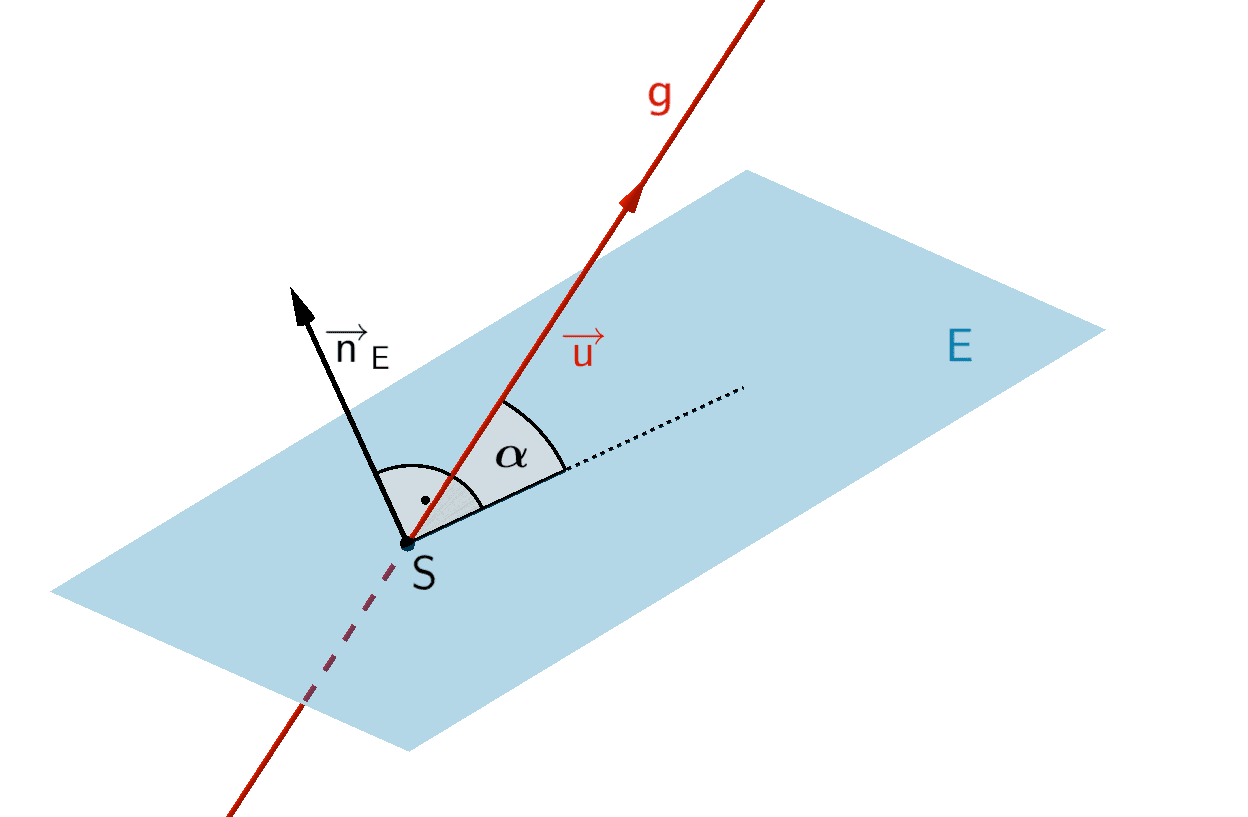
Die Gerade \(g\) schneidet die Ebene \(E\) im Schnittpunkt \(S\) unter dem Schnittwinkel \(\alpha\).
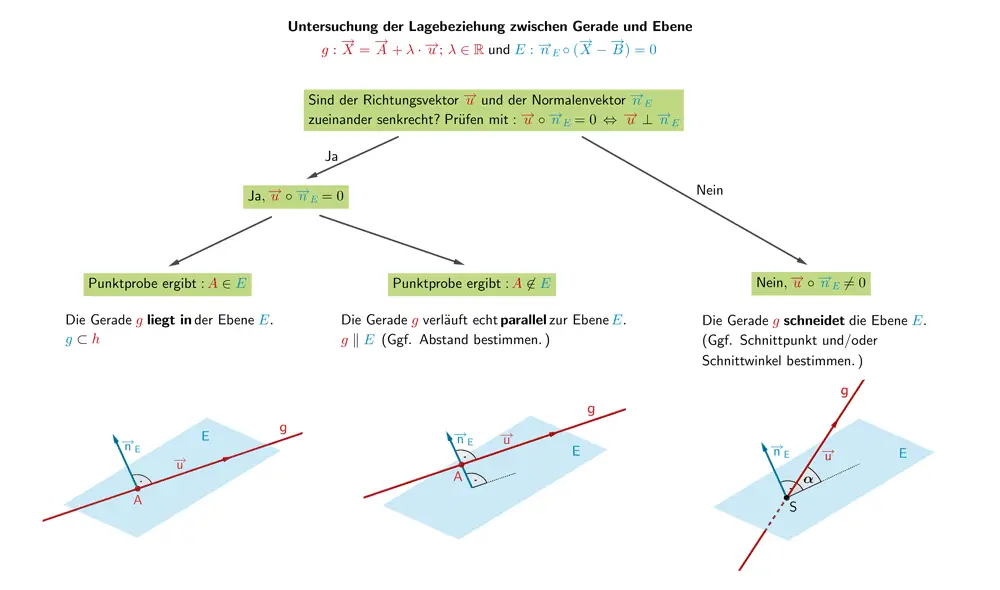
Untersuchung der Lagebeziehung zwischen Gerade und Ebene
Für die Untersuchung der gegenseitigen Lage zwischen einer Gerade \(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}; \; \lambda \in \mathbb R\) und einer Ebene \(E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{B}) = 0\) überprüft man mithilfe des Skalarprodukts, ob der Richtungsvektor \(\overrightarrow{u}\) der Gerade \(g\) und der Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\) zueinander senkrecht sind (vgl. Abiturskript - 2.1.3 Skalarprodukt von Vektoren, Anwendungen des Skalarprodukts).
Liegt die Gleichung der Ebene \(E\) in der Parameterform vor, ermittelt man zunächst mithilfe des Vektorprodukts der Richtungsvektoren einen Normalenvektor \(\overrightarrow{n}_{E}\) (vgl. Abiturskript - 2.2.4 Umwandlung: Parameterform - Normalenform).
![]() Untersuchung der Lagebeziehung zwischen Gerade und Ebene
Untersuchung der Lagebeziehung zwischen Gerade und Ebene
Man überprüft zuerst die Gültigkeit der Gleichung \(\overrightarrow{u} \circ \overrightarrow{n}_{E} = 0\).
Gilt \(\overrightarrow{u} \circ \overrightarrow{n}_{E} = 0\) sind der Richtungsvektor \(\overrightarrow{u}\) der Gerade \(g\) und der Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\) zueinander senkrecht. Die Gerade \(g\) kann somit in der Ebene \(E\) liegen oder (echt) parallel zur Ebene \(E\) verlaufen. Erfüllt der Aufpunkt \(A\) der Gerade \(g\) die Gleichung der Ebene \(E\) (Punktprobe), liegt die Gerade \(g\) in der Ebene \(E\). Andernfalls verläuft die Gerade \(g\) in einem Abstand parallel zur Ebene \(E\) (vgl. Abiturskript - 2.4.5 Abstand Gerade - Ebene).
Gilt \(\overrightarrow{u} \circ \overrightarrow{n}_{E} \neq 0\) schneidet die Gerade \(g\) die Ebene \(E\) in einem Schnittpunkt \(S\) unter einem Schnittwinkel \(\alpha\) (vgl. Abiturskript - 2.5.2 Schnittwinkel zwischen Gerade und Ebene).
Bestimmung des Schnittpunkts einer Geraden und einer Ebene
Für die Berechnung des Schnittpunkts \(S\) einer Gerade \(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}; \; \lambda \in \mathbb R\) und einer Ebene \(E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\) setzt man die Koordinaten des Ortsvektors \(\overrightarrow{X}\) der Geradengleichung von \(g\) in die Ebenengleichung von \(E\) ein. Anschließend löst man die Gleichung nach dem Parameter \(\lambda\) auf. Ergibt sich eine eindeutige Lösung für \(\lambda\), erhält man den Ortsvektor des Schnittpunktes \(S\), indem man den ermittelten Wert für \(\lambda\) in die Geradengleichung von \(g\) einsetzt.
\[\begin{align*}&g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u} \\[0.8em] &g \colon \begin{pmatrix} x_{1} \\ x_{2} \\ x_{3} \end{pmatrix} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} + \lambda \cdot \begin{pmatrix} u_{1} \\ u_{2} \\ u_{3} \end{pmatrix} \end{align*}\]
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
\[g \cap E \colon n_{1} \cdot (a_{1} + \lambda u_{1}) + n_{2} \cdot (a_{2} + \lambda u_{2}) + n_{3} \cdot (a_{3} + \lambda u_{3}) + n_{0} = 0\]
Der Ansatz zur Bestimmung des Schnittpunkts kann generell auch angewendet werden, um die gegenseitige Lage zwischen einer Gerade \(g\) und einer Ebene \(E\) zu untersuchen.
Liefert das Ergebnis der Gleichung eine
- wahre Aussage, liegt die Gerade \(g\) in der Ebene \(E\) (\(g \subset E\)).
- falsche Aussage, verläuft die Gerade \(g\) (echt) parallel zur Ebene \(E\) (\(g \parallel E\)).
- eindeutige Lösung für \(\lambda\), schneidet die Gerade \(g\) die Ebene \(E\) im Schnittpunkt \(S\).
Ist die Gleichung einer Ebene in der Parameterform gegeben, ist es zweckmäßig, diese in die Normalenform in Koordinatendarstellung umzuwandeln (vgl. Abiturskript - 2.2.4 Umwandlung: Parameterform - Normalenform). Andernfalls muss unter größerem Rechenaufwand ein lineares Gleichungssystem mit drei Gleichungen und drei unbekannten gelöst werden, um die gegenseitige Lage zwischen einer Gerade und einer Ebene bzw. einen Schnittpunkt zu ermitteln.
Beispiel:
Berechnen Sie den Schnittpunkt \(S\) der Gerade \(g \colon \overrightarrow{X} = \begin{pmatrix} -1 \\ 4 \\ 0 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 3 \\ 7 \end{pmatrix}; \; \lambda \in \mathbb R\) und der Ebene \(E \colon 2x_{1} - 3x_{2} + 5x_{3} - 14 = 0\).
\[g \colon \overrightarrow{X} = \begin{pmatrix} -1 \\ 4 \\ 0 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 3 \\ 7 \end{pmatrix}; \; \lambda \in \mathbb R\]
\[E \colon 2x_{1} - 3x_{2} + 5x_{3} - 14 = 0\]
Die Koordinaten des Ortsvektors \(\overrightarrow{X}\) der Geradengleichung von \(g\) in die Ebenengleichung von \(E\) einsetzen und die Gleichung nach dem Parameter \(\lambda\) auflösen:
\[\begin{align*}g \cap E \colon 2 \cdot (-1 + \lambda) - 3 \cdot (4 + 3\lambda) + 5 \cdot (0 + 7\lambda) - 14 &= 0 \\[0.8em] -2 + 2\lambda - 12 - 9\lambda + 35\lambda - 14 &= 0 \\[0.8em] 28\lambda - 28 &= 0 & &| + 28 \\[0.8em] 28\lambda &= 28 & &| : 28 \\[0.8em] \lambda &= 1 \end{align*}\]
Parameterwert \(\lambda = 1\) in die Gleichung der Gerade \(g\) einsetzen und die Koordinaten des Schnittpunkts \(S\) berechnen:
\[\overrightarrow{S} = \begin{pmatrix} -1 \\ 4 \\ 0 \end{pmatrix} + 1 \cdot \begin{pmatrix} 1 \\ 3 \\ 7 \end{pmatrix} = \begin{pmatrix} 0 \\ 7 \\ 7 \end{pmatrix}\]
\[\Longrightarrow \quad S(0|7|7)\]
Beispielaufgabe
Gegeben seien die Punkte \(A(5|1|3)\) und \(B(b|-2b|7)\) mit \(b \in \mathbb R\) sowie die Ebene \(E \colon 3x_{1} + 2x_{2} + 5x_{3} - 6 = 0\).
Es gibt eine Gerade \(g\) durch die Punkte \(A\) und \(B\), die parallel zur Ebene \(E\) verläuft. Bestätigen Sie diese Aussage durch Rechnung und ermitteln Sie eine Gleichung der Gerade \(g\).
Geben Sie eine Gleichung der Gerade \(h\) an, welche in der Ebene \(E\) liegt und parallel zur Gerade \(g\) verläuft.
Nachweis und Gleichung der Gerade \(g\)
\(A(5|1|3)\), \(B(b|-2b|7)\)
\[E \colon 3x_{1} + 2x_{2} + 5x_{3} - 6 = 0\]
\[A, B \in g\,, \; g \parallel E\]
Die Gerade \(g\) verläuft (echt) parallel zur Ebene \(E\), wenn keiner der Punkte \(A\) und \(B\) in der Ebene \(E\) liegt und der Verbindungsvektor \(\overrightarrow{AB}\) senkrecht zum Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\) ist.
\[\left. \begin{align*} &A, B \notin E \\[0.8em] &\overrightarrow{AB} \circ \overrightarrow{n}_{E} = 0 \enspace \Longleftrightarrow \enspace \overrightarrow{AB} \perp \overrightarrow{n}_{E} \end{align*} \right\} \enspace \Rightarrow \enspace g \parallel E\]
Der Punkt \(B(b|-2b|7)\) kann für einen bestimmten Wert des Parameters \(b\) in der Ebene \(E\) liegen. Deshalb weist man nach, dass der Punkt \(A\) nicht in der Ebene \(E\) liegt, und dass für einen bestimmten Wert des Parameters \(b\) ein Verbindungsvektor \(\overrightarrow{AB} \perp \overrightarrow{n}_{E}\) existiert. Der zugehörige Punkt \(B\) kann dann ebenfalls nicht in der Ebene \(E\) liegen.
Punktprobe \(A \in E\):
\[A(5|1|3)\]
\[E \colon 3x_{1} + 2x_{2} + 5x_{3} - 6 = 0\]
\[\begin{align*}3 \cdot 5 + 2 \cdot 1 + 5 \cdot 3 - 6 &= 0 \\[0.8em] 26 = 0 \quad (\text{f}) \end{align*}\]
\[\Longrightarrow \quad A \notin E\]
Nachweis, dass ein Verbindungsvektor \(\overrightarrow{AB} \perp \overrightarrow{n}_{E}\) existiert:
\(A(5|1|3)\), \(B(b|-2b|7)\)
\[E \colon 3x_{1} + 2x_{2} + 5x_{3} - 6 = 0\]
Der Normalenvektor \(\overrightarrow{n}_{E}\) kann der Ebenengleichung in Normalenform in Koordinatendarstellung direkt entnommen werden.
\[E \colon 3x_{1} + 2x_{2} + 5x_{3} - 6 = 0 \quad \Longrightarrow \quad \overrightarrow{n}_{E} = \begin{pmatrix} 3 \\ 2 \\ 5 \end{pmatrix}\]
Verbindungsvektor \(\overrightarrow{AB}\) in Abhängigkeit des Parameters \(b\) formulieren:
\[\overrightarrow{AB} = \overrightarrow{B} - \overrightarrow{A} = \begin{pmatrix} b \\ -2b \\ 7 \end{pmatrix} - \begin{pmatrix} 5 \\ 1 \\ 3 \end{pmatrix} = \begin{pmatrix} b - 5 \\ -2b - 1 \\ 4 \end{pmatrix}\]
Wert des Parameters \(b\) unter der Bedingung \(\overrightarrow{AB} \perp \overrightarrow{n}_{E}\) berechnen:
\[\overrightarrow{AB} \perp \overrightarrow{n}_{E} \enspace \Longleftrightarrow \enspace \overrightarrow{AB} \circ \overrightarrow{n}_{E} = 0\]
\[\begin{align*} \begin{pmatrix} b - 5 \\ -2b - 1 \\ 4 \end{pmatrix} \circ \begin{pmatrix} 3 \\ 2 \\ 5 \end{pmatrix} &= 0 \\[0.8em] 3 \cdot (b - 5) + 2 \cdot (-2b - 1) + 20 &= 0 \\[0.8em] 3b - 15 - 4b - 2 + 20 &= 0 \\[0.8em] -b + 3 &= 0 & &| + b \\[0.8em] 3 = b \end{align*}\]
Für den Parameterwert \(b = 3\) des Punktes \(B(b|-2b|7)\) gilt: \(\overrightarrow{AB} \perp \overrightarrow{n}_{E}\) und damit \(\overrightarrow{AB} \parallel E\). Folglich gibt es eine Gerade \(g\) durch die Punkte \(A\) und \(B\), die parallel zur Ebene \(E\) verläuft.
Gleichung der Gerade \(g\):
Es sei \(A(5|1|3)\) der Aufpunkt der Gerade \(g\).
\[g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{AB}\,; \; \lambda \in \mathbb R\]
\[\overrightarrow{AB} = \begin{pmatrix} b - 5 \\ -2b - 1 \\ 4 \end{pmatrix} = \begin{pmatrix} 3 - 5 \\ -2 \cdot 3 - 1 \\ 4 \end{pmatrix} = \begin{pmatrix} -2 \\ -7 \\ 4 \end{pmatrix}\]
\[\Longrightarrow \quad g \colon \overrightarrow{X} = \begin{pmatrix} 5 \\ 1 \\ 3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -2 \\ -7 \\ 4 \end{pmatrix}; \; \lambda \in \mathbb R\]
Gleichung der Gerade \(h\)
\[g \colon \overrightarrow{X} = \begin{pmatrix} 5 \\ 1 \\ 3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -2 \\ -7 \\ 4 \end{pmatrix}; \; \lambda \in \mathbb R\]
\[E \colon 3x_{1} + 2x_{2} + 5x_{3} - 6 = 0\]
\[h \parallel g\,, \; h \subset E\]
Die Gerade \(h\) ist nicht eindeutig festgelegt. Die Parallelität der Geraden \(h\) und \(g\) bestimmt die Orientierung der Gerade \(h\). Da als Aufpunkt der Gerade \(h\) jeder Punkt in der Ebene \(E\) in Frage kommt, gibt es unendlich viele Geraden, welche die genannten Bedingungen erfüllen. Eine Gleichung einer möglichen Gerade \(h\) soll angegeben werden.
Als Aufpunkt der Gerade \(h\) bietet sich einer der Spurpunkte der Ebene \(E\) an, z.B. der Schnittpunkt \(S_{x_{2}}\) der Ebene \(E\) mit der \(x_{2}\)-Achse (vgl. Abiturskript - 2.2.3 Ebenengleichung in Normalenform, Spurgerade einer Ebene)
Da die Gerade \(h\) parallel zur Gerade \(g\) verlaufen soll, dient der Richtungsvektor der Gerade \(g\) als Richtungsvektor der Gerade \(h\).
Schnittpunkt \(S_{x_{2}}\) der Ebene \(E\) mit der \(x_{2}\)-Achse ermitteln:
\[S_{x_{2}}(0|s_{2}|0)\]
\[E \colon 3x_{1} + 2x_{2} + 5x_{3} - 6 = 0\]
\[S_{x_{2}} \in E \quad \Longrightarrow \quad 2s_{2} - 6 = 0 \quad \Longleftrightarrow \quad s_{2} = \frac{6}{2} = 3\]
\[\Longrightarrow \quad S_{x_{2}}(0|3|0)\]
Gleichung der Gerade \(h\) angeben:
\[h \colon \overrightarrow{X} = \begin{pmatrix} 0 \\ 3 \\ 0 \end{pmatrix} + \mu \cdot \begin{pmatrix} -2 \\ -7 \\ 4 \end{pmatrix}; \; \mu \in \mathbb R\]
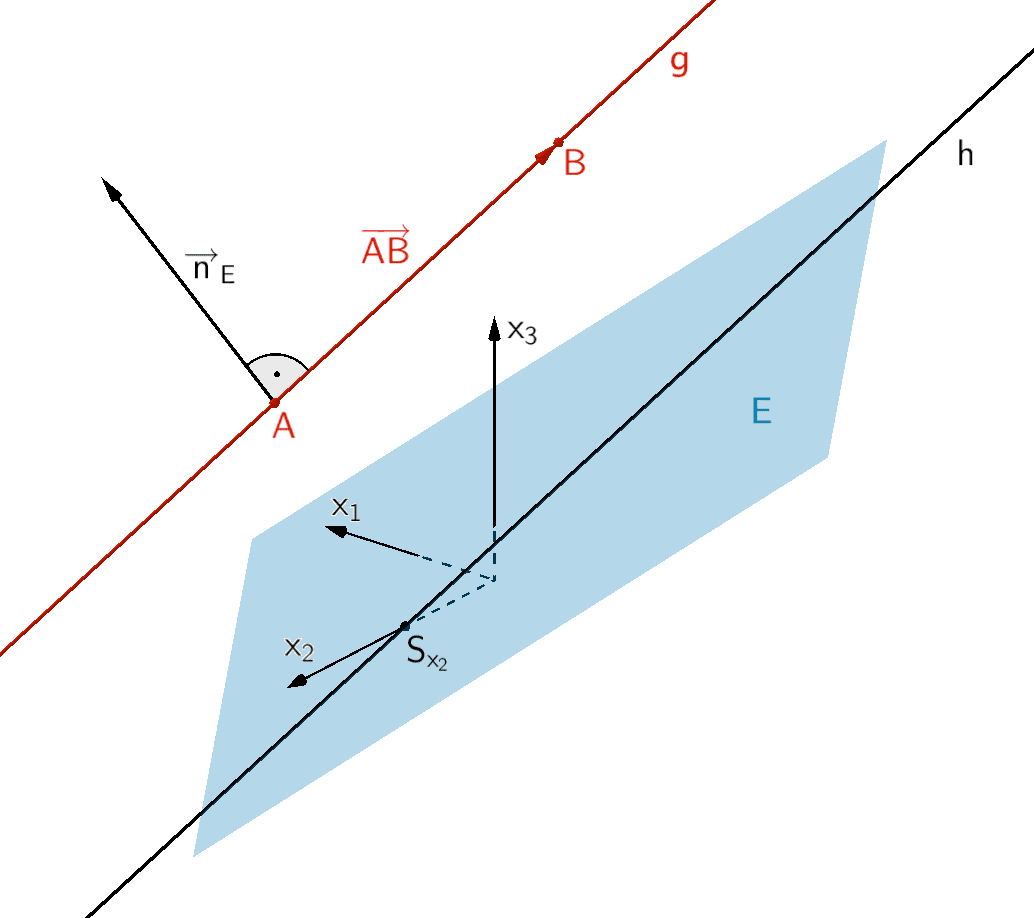
Gerade \(g\) mit den Eigenschaften \(A, B \in g\) und \(g \parallel E\), Gerade \(h\) mit den Eigenschaften \(S_{x_{2}} \in h\) und \(h \parallel g\), Ebene \(E\)