Abstand zweier parallelen Geraden
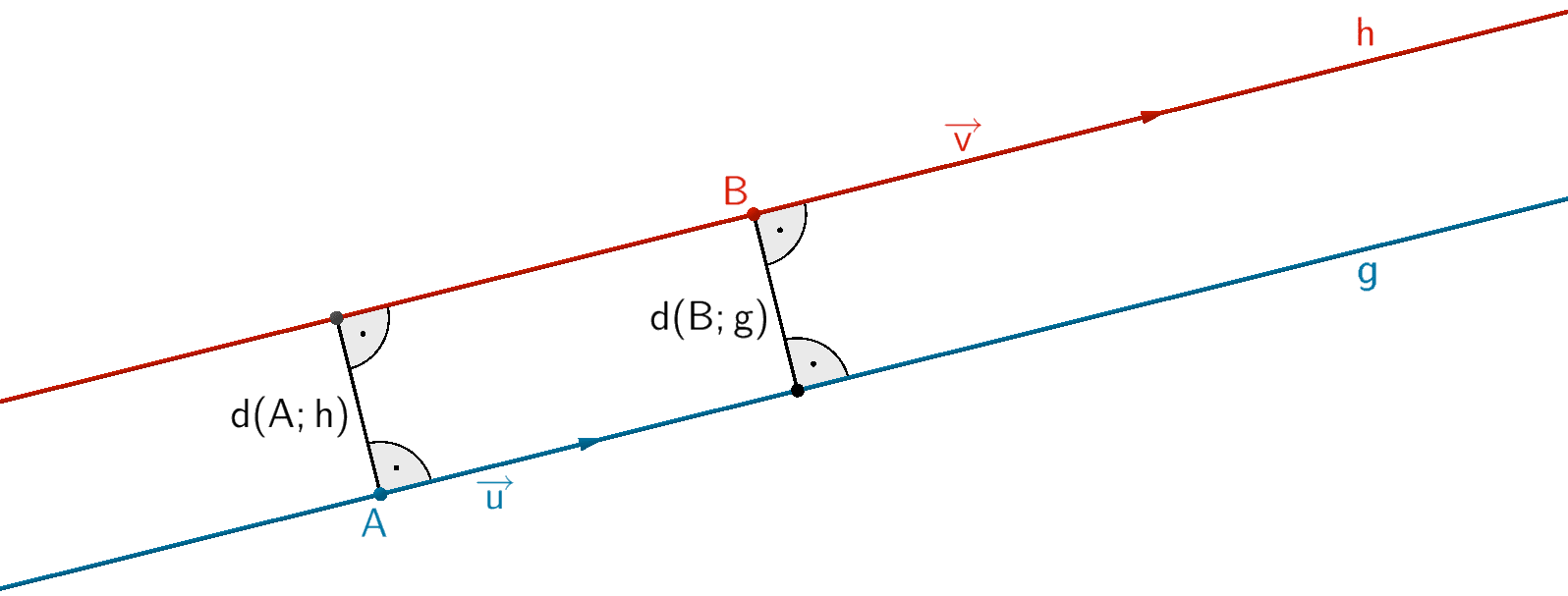
Die Abstandsbestimmung zweier (echt) parallelen Geraden \(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}\,; \; \lambda \in \mathbb R\) und \(h \colon \overrightarrow{X} = \overrightarrow{B} + \mu \cdot \overrightarrow{v}\,; \; \mu \in \mathbb R\) lässt sich auf die Abstandsbestimmung eines beliebigen Punktes \(P \in h\) zur Geraden \(g\) bzw. \(P \in g\) zur Geraden \(h\) zurückführen (vgl. Abiturskript - 2.4.1 Abstand Punkt - Gerade). Zweckmäßig wählt man den Aufpunkt \(B\) der Geradengleichung von \(h\) bzw. den Aufpunkt \(A\) der Geradengleichung von \(g\).
\(d(h;g) = d(B;g)\) (Abstand der Geraden \(h\) von der Geraden \(g\))
bzw.
\(d(g;h) = d(A;h)\) (Abstand der Geraden \(g\) von der Geraden \(h\))
Je nach Aufgabenstellung ist vorab der Abstandsbestimmung ggf. die Parallelität der Geraden \(g\) und \(h\) nachzuweisen (vgl. Abiturskript - 2.3.1 Lagebeziehung von Geraden).
Beispielaufgabe
Gegeben seien die Geraden \(g \colon \overrightarrow{X} = \begin{pmatrix} 2 \\ 2 \\ 1 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix}; \; \lambda \in \mathbb R\) und \(h \colon \overrightarrow{X} = \begin{pmatrix} -2 \\ 4 \\ 2 \end{pmatrix} + \mu \cdot \begin{pmatrix} -4 \\ 2 \\ -2 \end{pmatrix}; \; \mu \in \mathbb R\).
Weisen Sie nach, dass die Geraden \(g\) und \(h\) im konstanten Abstand \(d\) zueinander verlaufen und berechnen Sie den Abstand \(d\).
\[g \colon \overrightarrow{X} = \begin{pmatrix} 2 \\ 2 \\ 1 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix}; \; \lambda \in \mathbb R\]
\[h \colon \overrightarrow{X} = \begin{pmatrix} -2 \\ 4 \\ 2 \end{pmatrix} + \mu \cdot \begin{pmatrix} -4 \\ 2 \\ -2 \end{pmatrix}; \; \mu \in \mathbb R\]
Nachweis, dass \(g\) und \(h\) im konstanten Abstand \(d\) zueinander verlaufen
Die Geraden \(g\) und \(h\) verlaufen in einem konstanten Abstand \(d\) zueinander, wenn sie parallel zueinander sind. Für den Nachweis der Parallelität \(g \parallel h\) betrachtet man die Richtungsvektoren der Geraden \(g\) und \(h\) (vgl. Abiturskript - 2.3.1 Lagebeziehung von Geraden).
\[\begin{pmatrix} -4 \\ 2 \\ -2 \end{pmatrix} = (-2) \cdot \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix}\]
\(\Longrightarrow \quad\)Die Richtiungsvektoren der Geraden \(g\) und \(h\) sind linear abhängig (vgl. Abiturskript - 2.1.2 Lineare (Un-)Abhängigkeit von Vektoren). Folglich können die Geraden \(g\) und \(h\) (echt) parallel oder identisch sein.
Punktprobe:
Man überprüft beispielsweise, ob der Aufpunkt \(B(-2|4|2)\) der Geradengleichung von \(h\) die Gleichung der Geraden \(g\) erfüllt.
\[B \in g \colon \begin{pmatrix} -2 \\ 4 \\ 2 \end{pmatrix} = \begin{pmatrix} 2 \\ 2 \\ 1 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix}\]
\[\Longrightarrow \enspace \left\{ \begin{align*} -2 = 2 + 2\lambda \enspace &\Longrightarrow \enspace \lambda = -2 \\[0.8em] \enspace \; 4 = 2 - \enspace \lambda \enspace &\Longrightarrow \enspace \lambda = -2 \\[0.8em] \enspace \; 2 = 1 + \enspace \lambda \enspace &\Longrightarrow \enspace \lambda = \enspace \; 1 \end{align*} \right\} \enspace \Large{\text{↯}}\]
\[\Longrightarrow \quad B \notin g \quad \Longrightarrow \quad g \parallel h\]
\(\Longrightarrow \quad\)\(g\) und \(h\) verlaufen im konstanten Abstand \(d\) zueinander.
Abstand \(d\) der Geraden \(g\) und \(h\)
Die Bestimmung des Abstands \(d(h;g)\) der Geraden \(g\) und \(h\) lässt sich auf die Bestimmung des Abstands eines beliebigen Punktes \(P \in h\) zu der Geraden \(g\) zurückführen (vgl. Abiturskript - 2.4.1 Abstand Punkt - Gerade). Es ist zweckmäßig, hierfür den bereits bekannten Aufpunkt \(B(-2|4|2)\) der Geraden \(h\) zu wählen.
\[d(h;g) = d(B;g)\]
1. Möglichkeit: Skalarprodukt orthogonaler (senkrechter) Vektoren anwenden
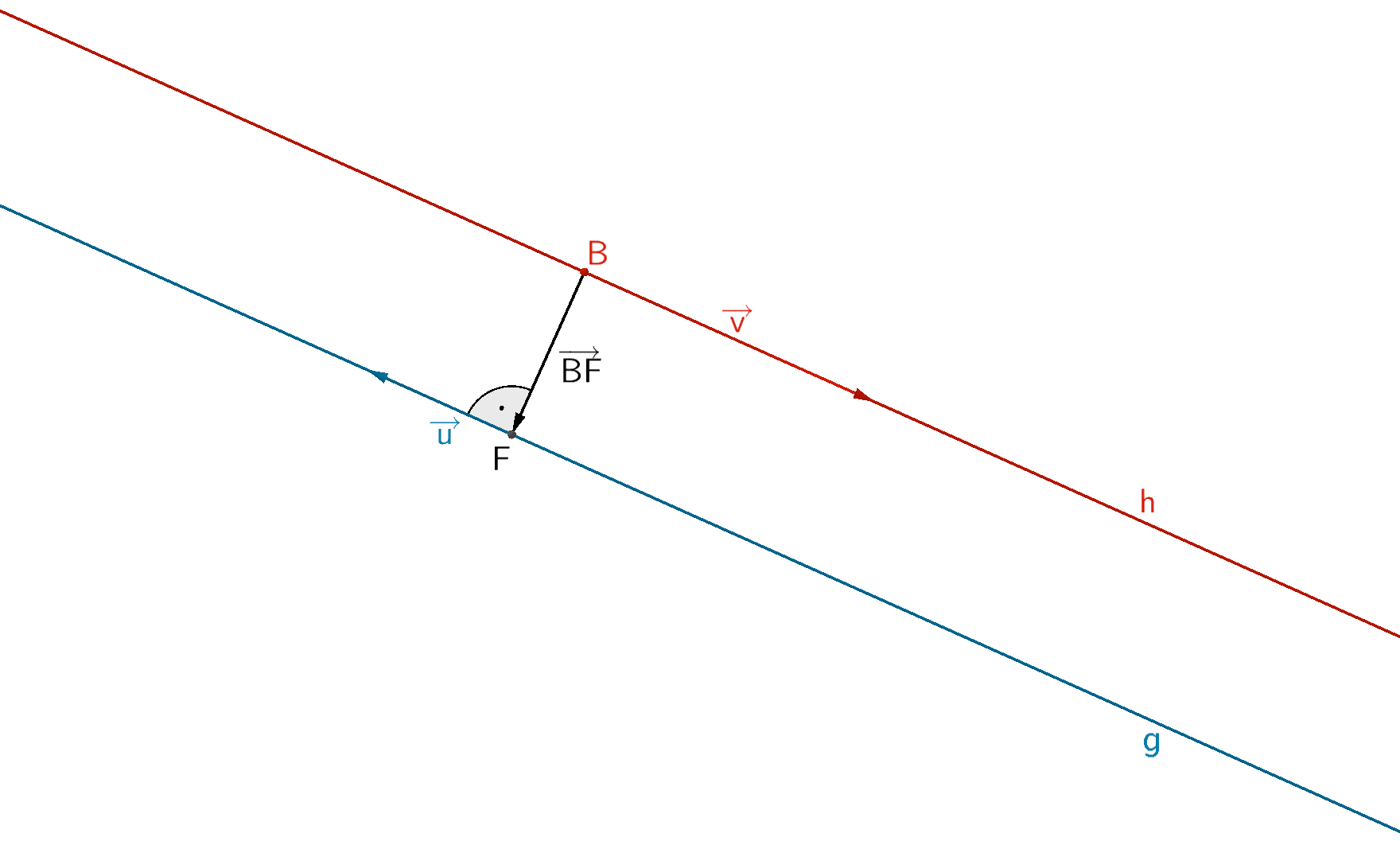
Es sei \(F\) der Lotfußpunkt des Lotes des Punktes \(B\) auf die Gerade \(g\).
\[g \colon \overrightarrow{X} = \begin{pmatrix} 2 \\ 2 \\ 1 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix}; \; \lambda \in \mathbb R\]
\[h \colon \overrightarrow{X} = \begin{pmatrix} -2 \\ 4 \\ 2 \end{pmatrix} + \mu \cdot \begin{pmatrix} -4 \\ 2 \\ -2 \end{pmatrix}; \; \mu \in \mathbb R\]
\[B(-2|4|2)\]
\[d(h;g) = d(B;g) = \vert \overrightarrow{BF} \vert\]
Verbindungsvektor \(\overrightarrow{BF}\) in Abhängigkeit des Parameters \(\lambda\) der Gleichung der Geraden \(g\) beschreiben:
\[F \in g \colon \overrightarrow{F} = \begin{pmatrix} 2 \\ 2 \\ 1 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix} = \begin{pmatrix} 2 + 2\lambda \\ 2 - \lambda \\ 1 + \lambda \end{pmatrix}\]
\[\overrightarrow{BF} = \overrightarrow{F} - \overrightarrow{B} =\begin{pmatrix} 2 + 2\lambda \\ 2 - \lambda \\ 1 + \lambda \end{pmatrix} - \begin{pmatrix} -2 \\ 4 \\ 2 \end{pmatrix} = \begin{pmatrix} 4 + 2\lambda \\ -2 - \lambda \\ -1 + \lambda \end{pmatrix}\]
Skalarprodukt der ortogonalen Vektoren \(\overrightarrow{u}\) (Richtungsvektor von \(g\)) und \(\overrightarrow{BF}\) anwenden (vgl. Abiturskript - 2.1.3 Skalarprodukt von Vektoren, Anwendungen des Skalarprodukts):
\[\begin{align*}\overrightarrow{u} \circ \overrightarrow{BF} &= 0 \\[0.8em] \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix} \circ \begin{pmatrix} 4 + 2\lambda \\ -2 - \lambda \\ -1 + \lambda \end{pmatrix} &= 0 \\[0.8em] 2 \cdot (4 + 2\lambda) + (-1) \cdot (-2 - \lambda) + 1 \cdot (-1 + \lambda) &= 0 \\[0.8em] 8 + 4\lambda + 2 + \lambda - 1 + \lambda &= 0 \\[0.8em] 9 + 6\lambda &= 0 & &| - 9 \\[0.8em] 6\lambda &= -9 & &| : 6 \\[0.8em] \lambda &= -\frac{9}{6} \\[0.8em] \lambda &= -1{,}5 \end{align*}\]
Verbindungsvektor \(\overrightarrow{BF}\) berechnen:
\[\overrightarrow{BF} = \begin{pmatrix} 4 + 2\lambda \\ -2 - \lambda \\ -1 + \lambda \end{pmatrix} = \begin{pmatrix} 4 + 2 \cdot (-1{,}5) \\ -2 - (-1{,}5) \\ -1 + (-1{,}5) \end{pmatrix} = \begin{pmatrix} 1 \\ -0{,}5 \\ -2{,}5 \end{pmatrix}\]
Abstand \(d(h;g)\) der Geraden \(g\) und \(h\) berechnen:
\[\begin{align*}d(h;g) &= d(B;g) \\[0.8em] &= \vert \overrightarrow{BF} \vert \\[0.8em] &= \left| \begin{pmatrix} 1 \\ -0{,}5 \\ -2{,}5 \end{pmatrix} \right| \\[0.8em] &= \sqrt{1^{2} + (-0{,}5)^{2} + (-2{,}5)^{2}} \\[0.8em] &= \frac{\sqrt{30}}{2} \\[0.8em] &\approx 2{,}74\end{align*}\]
2. Möglichkeit: Hilfsebene aufstellen
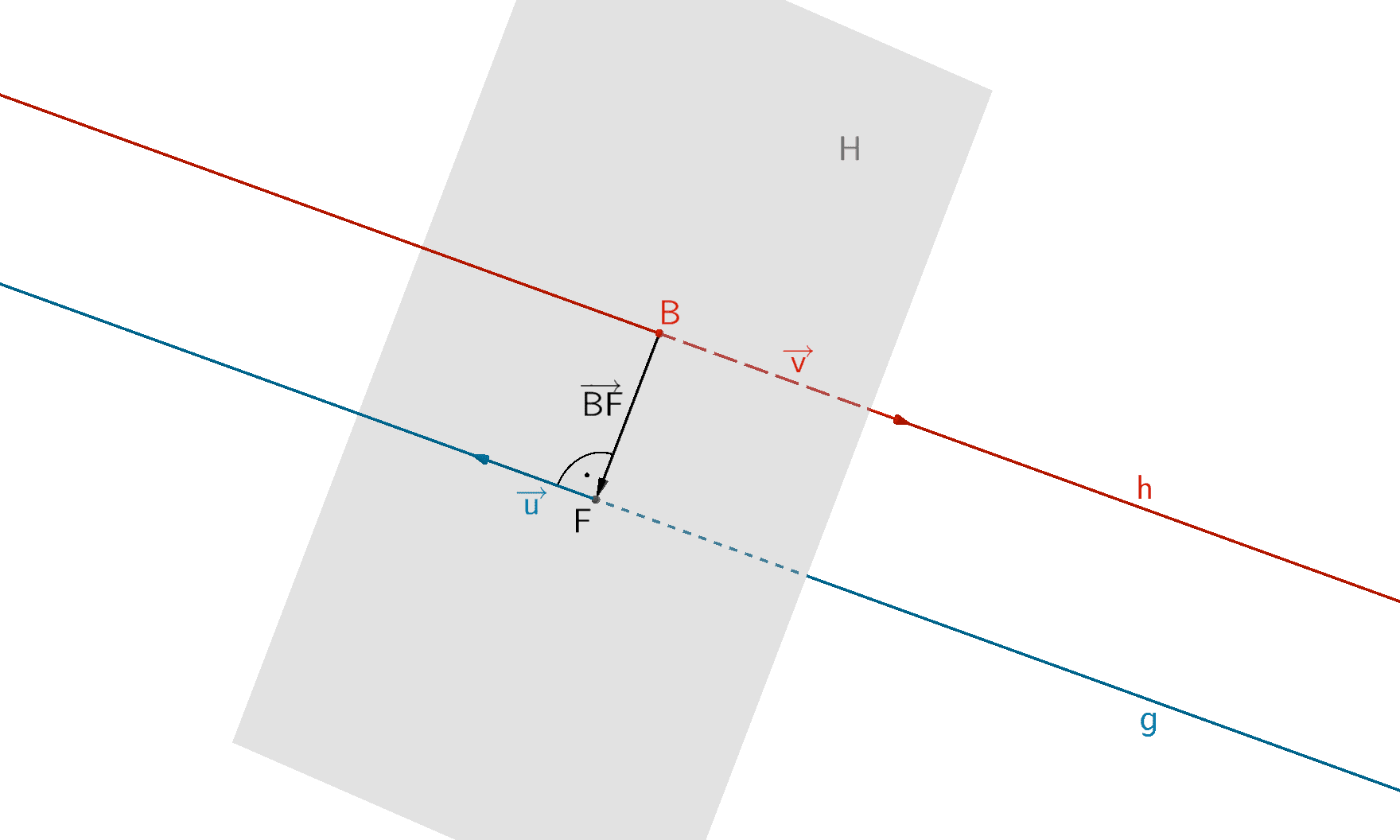
Es sei \(F\) der Lotfußpunkt des Lotes des Punktes \(B\) auf die Gerade \(g\).
\[g \colon \overrightarrow{X} = \begin{pmatrix} 2 \\ 2 \\ 1 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix}; \; \lambda \in \mathbb R\]
\[h \colon \overrightarrow{X} = \begin{pmatrix} -2 \\ 4 \\ 2 \end{pmatrix} + \mu \cdot \begin{pmatrix} -4 \\ 2 \\ -2 \end{pmatrix}; \; \mu \in \mathbb R\]
\[B(-2|4|2)\]
\[d(h;g) = d(B;g) = \vert \overrightarrow{BF} \vert\]
Gleichung der Hilfsebene \(H\) aufstellen:
\(B \in H\,, \; g \perp H\)
\[H \colon \overrightarrow{u} \circ (\overrightarrow{X} - \overrightarrow{B}) = 0\]
\[H \colon \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} -2 \\ 4 \\ 2 \end{pmatrix} \right] = 0\]
\[\begin{align*} \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} -2 \\ 4 \\ 2 \end{pmatrix} \right] &= 0 \\[0.8em] 2 \cdot (x_{1} + 2) + (-1) \cdot (x_{2} - 4) + 1 \cdot (x_{3} - 2) &= 0 \\[0.8em] 2x_{1} + 4 - x_{2} + 4 + x_{3} - 2 &= 0 \\[0.8em] 2x_{1} - x_{2} + x_{3} + 6 &= 0 \end{align*}\]
\[H \colon 2x_{1} - x_{2} + x_{3} + 6 = 0\]
Verbindungsvektor \(\overrightarrow{BF}\) in Abhängigkeit des Parameters \(\lambda\) der Gleichung der Geraden \(g\) beschreiben:
\[F \in g \colon \overrightarrow{F} = \begin{pmatrix} 2 \\ 2 \\ 1 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix} = \begin{pmatrix} 2 + 2\lambda \\ 2 - \lambda \\ 1 + \lambda \end{pmatrix}\]
\[\overrightarrow{BF} = \overrightarrow{F} - \overrightarrow{B} =\begin{pmatrix} 2 + 2\lambda \\ 2 - \lambda \\ 1 + \lambda \end{pmatrix} - \begin{pmatrix} -2 \\ 4 \\ 2 \end{pmatrix} = \begin{pmatrix} 4 + 2\lambda \\ -2 - \lambda \\ -1 + \lambda \end{pmatrix}\]
Geraden \(g\) mit der Hilfsebene \(H\) schneiden (vgl. Abiturskript - 2.3.2 Lagebeziehung von Gerade und Ebene, Bestimmung des Schnittpunkts):
\[g \colon \overrightarrow{X} = \begin{pmatrix} 2 \\ 2 \\ 1 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix}; \; \lambda \in \mathbb R\]
\[H \colon 2x_{1} - x_{2} + x_{3} + 6 = 0\]
\[\begin{align*} g \cap H \colon 2 \cdot (2 + 2\lambda) - (2 - \lambda) + 1 + \lambda + 6 &= 0 \\[0.8em] 4 + 4\lambda - 2 + \lambda + 1 + \lambda + 6 &= 0 \\[0.8em] 9 + 6\lambda &= 0 & &| - 9 \\[0.8em] 6\lambda &= -9 & &| : 6 \\[0.8em] \lambda &= -\frac{9}{6} \\[0.8em] \lambda &= -1{,}5 \end{align*}\]
Verbindungsvektor \(\overrightarrow{BF}\) berechnen:
\[\overrightarrow{BF} = \begin{pmatrix} 4 + 2\lambda \\ -2 - \lambda \\ -1 + \lambda \end{pmatrix} = \begin{pmatrix} 4 + 2 \cdot (-1{,}5) \\ -2 - (-1{,}5) \\ -1 + (-1{,}5) \end{pmatrix} = \begin{pmatrix} 1 \\ -0{,}5 \\ -2{,}5 \end{pmatrix}\]
Abstand \(d(h;g)\) der Geraden \(g\) und \(h\) berechnen:
\[\begin{align*}d(h;g) &= d(B;g) \\[0.8em] &= \vert \overrightarrow{BF} \vert \\[0.8em] &= \left| \begin{pmatrix} 1 \\ -0{,}5 \\ -2{,}5 \end{pmatrix} \right| \\[0.8em] &= \sqrt{1^{2} + (-0{,}5)^{2} + (-2{,}5)^{2}} \\[0.8em] &= \frac{\sqrt{30}}{2} \\[0.8em] &\approx 2{,}74\end{align*}\]
3. Möglichkeit: Differentialrechnung anwenden (Extremwertaufgabe)
![Strecke [BX] zwischen dem Aufpunkt B der Geraden h und einem beliebigen Punkt X ∈ g Strecke [BX] zwischen dem Aufpunkt B der Geraden h und einem beliebigen Punkt X ∈ g](/images/stories/abi_check/geometrie/Abstand_paralleler_Geraden_Bsp3.png)
Es sei \(F\) der Lotfußpunkt des Lotes des Punktes \(B\) auf die Gerade \(g\).
\[g \colon \overrightarrow{X} = \begin{pmatrix} 2 \\ 2 \\ 1 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix}; \; \lambda \in \mathbb R\]
\[h \colon \overrightarrow{X} = \begin{pmatrix} -2 \\ 4 \\ 2 \end{pmatrix} + \mu \cdot \begin{pmatrix} -4 \\ 2 \\ -2 \end{pmatrix}; \; \mu \in \mathbb R\]
\[B(-2|4|2)\]
\[d(h;g) = d(B;g) = \vert \overrightarrow{BF} \vert\]
Verbindungsvektor \(\overrightarrow{RX}\) in Abhängigkeit des Parameters \(\lambda\) der Gleichung der Geraden \(g\) beschreiben:
\[g \colon \overrightarrow{X} = \begin{pmatrix} 2 \\ 2 \\ 1 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix} = \begin{pmatrix} 2 + 2\lambda \\ 2 - \lambda \\ 1 + \lambda \end{pmatrix}\]
\[\overrightarrow{BX} = \overrightarrow{X} - \overrightarrow{B} = \begin{pmatrix} 2 + 2\lambda \\ 2 - \lambda \\ 1 + \lambda \end{pmatrix} - \begin{pmatrix} -2 \\ 4 \\ 2 \end{pmatrix} = \begin{pmatrix} 4 + 2\lambda \\ -2 - \lambda \\ -1 + \lambda \end{pmatrix}\]
Länge der Strecke \([BX]\) in Abhängigkeit des Parameters \(\lambda\) formulieren:
\[\begin{align*} \overline{BX} &= \vert \overrightarrow{BX} \vert \\[0.8em] &= \left| \begin{pmatrix} 4 + 2\lambda \\ -2 - \lambda \\ -1 + \lambda \end{pmatrix} \right| \\[0.8em] &= \sqrt{(4 + 2\lambda)^{2} + (-2 - \lambda)^{2} + (-1 + \lambda)^{2}} \\[0.8em] &= \sqrt{16 + 16\lambda + 4\lambda^{2} + 4 + 4\lambda + \lambda^{2} + 1 - 2\lambda + \lambda^{2}} \\[0.8em] &= \sqrt{6\lambda^{2} + 18\lambda + 21} \end{align*}\]
Notwendige Bedingung \(\overline{BX}'(\lambda) = 0\) für minimale Länge der Strecke \([BX]\) (vgl. Abiturskript - 1.5.2 Ableitungsregeln):
\[\begin{align*} \overline{BX}'(\lambda) &= 0 \\[0.8em] \left( \sqrt{6\lambda^{2} + 18\lambda + 21} \right)' &= 0 \\[0.8em] \frac{12\lambda + 18}{2 \cdot \sqrt{6\lambda^{2} + 18\lambda + 21}} &= 0 \end{align*}\]
\[\begin{align*}\Longrightarrow \quad 12\lambda + 18 &= 0 & &| - 18 \\[0.8em] 12\lambda &= -18 & &| : 18 \\[0.8em] \lambda &= -\frac{18}{12} \\[0.8em] \lambda &= -1{,}5\end{align*}\]
Verbindungsvektor \(\overrightarrow{BF}\) berechnen:
\[\overrightarrow{BF} = \begin{pmatrix} 4 + 2\lambda \\ -2 - \lambda \\ -1 + \lambda \end{pmatrix} = \begin{pmatrix} 4 + 2 \cdot (-1{,}5) \\ -2 - (-1{,}5) \\ -1 + (-1{,}5) \end{pmatrix} = \begin{pmatrix} 1 \\ -0{,}5 \\ -2{,}5 \end{pmatrix}\]
Abstand \(d(h;g)\) der Geraden \(g\) und \(h\) berechnen:
\[\begin{align*}d(h;g) &= d(B;g) \\[0.8em] &= \vert \overrightarrow{BF} \vert \\[0.8em] &= \left| \begin{pmatrix} 1 \\ -0{,}5 \\ -2{,}5 \end{pmatrix} \right| \\[0.8em] &= \sqrt{1^{2} + (-0{,}5)^{2} + (-2{,}5)^{2}} \\[0.8em] &= \frac{\sqrt{30}}{2} \\[0.8em] &\approx 2{,}74\end{align*}\]


