Abstand zweier windschiefen Geraden
Die Abstandsbestimmung zweier windschiefen Geraden \(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}; \; \lambda \in \mathbb R\) und \(h \colon \overrightarrow{X} = \overrightarrow{B} + \mu \cdot \overrightarrow{v}; \; \mu \in \mathbb R\) lässt sich auf die Abstandsbestimmung eines Punktes zu einer Hilfsebene zurückführen (vgl. Abiturskript - 2.4.4 Abstand Punkt - Ebene).
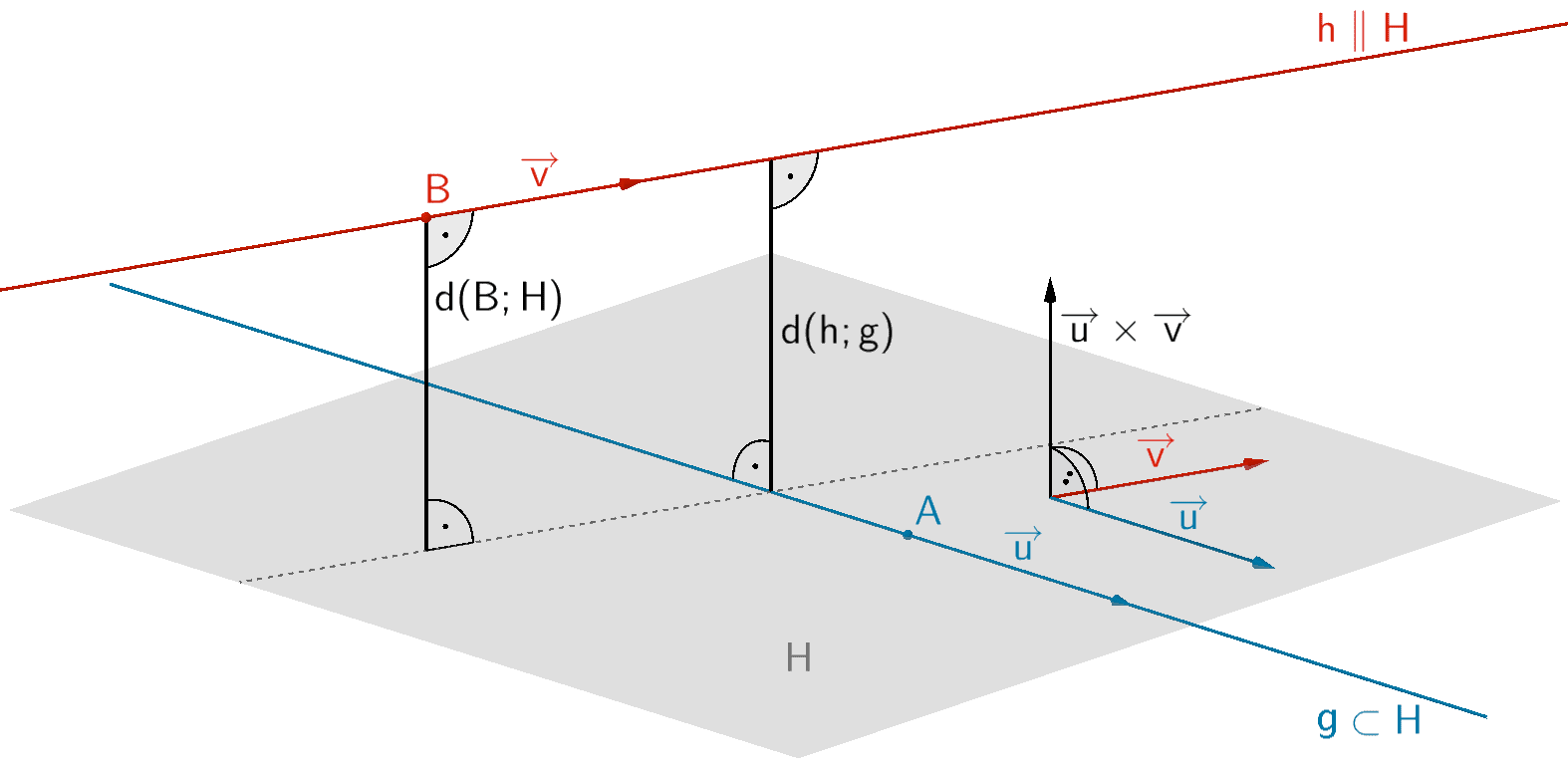
Hilfsebene \(H\), welche die Gerade \(g\) enthält \((g \subset H)\) und parallel zur Geraden \(h\) ist \((h \parallel H)\).
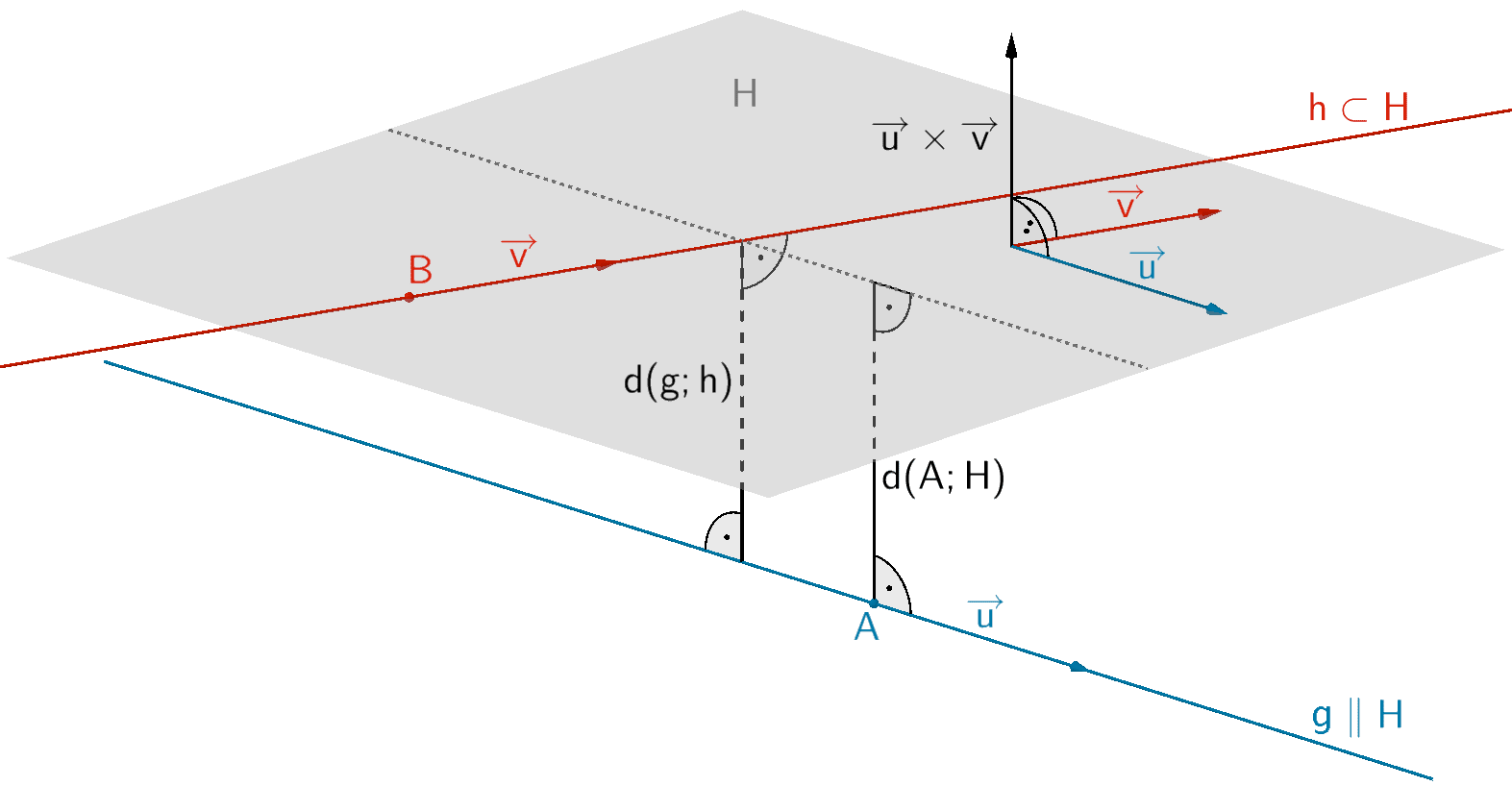
Hilfsebene \(H\), welche die Gerade \(h\) enthält \((h \subset H)\) und parallel zur Geraden \(g\) ist \((g \parallel H)\).
Man stellt eine Hilfsebene \(H\) auf, welche eine der beiden Geraden \(g\) oder \(h\) enthält und zur jeweils anderen Geraden parallel ist. Anschließend berechnet man den Abstand eines beliebigen Punktes der parallelen Geraden zur Hilfsebene. Zweckmäßig wählt man den Aufpunkt \(B\) der Geradengleichung von \(h\) bzw. den Aufpunkt \(A\) der Geradengleichung von \(g\).
Das Vektorprodukt der Richtungsvektoren \(\overrightarrow{u}\) und \(\overrightarrow{v}\) der Geraden \(g\) und \(h\) liefet einen Normalenvektor \(\overrightarrow{n}_{H}\) für die Gleichung der Hilfsebene \(H\) in Normalenform (vgl. Abiturskript - 2.1.4 Vektorprodukt, Anwendungen des Vektorprodukts).
\[\overrightarrow{n}_{H} = \overrightarrow{u} \times \overrightarrow{v}\]
Jedes Vielfache des Vektorprodukts \(\overrightarrow{u} \times \overrightarrow{v}\) ist ebenfalls ein Normalenvektor \(\overrightarrow{n}_{H}\) der Hilfsebene \(H\).
Als Aufpunkt der Hilfsebene \(H\) dient der Aufpunkt derjenigen Geraden \(g\) oder \(h\), welche in der Hilfsebene enthalten sein soll.
\[g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}; \; \lambda \in \mathbb R\]
\[h \colon \overrightarrow{X} = \overrightarrow{B} + \mu \cdot \overrightarrow{v}; \; \mu \in \mathbb R\]
\(H \colon \overrightarrow{n}_{H} \circ (\overrightarrow{X} - \overrightarrow{A})\) mit \(g \subset H, \, h \parallel H\)
\[g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}; \; \lambda \in \mathbb R\]
\[h \colon \overrightarrow{X} = \overrightarrow{B} + \mu \cdot \overrightarrow{v}; \; \mu \in \mathbb R\]
\(H \colon \overrightarrow{n}_{H} \circ (\overrightarrow{X} - \overrightarrow{B})\) mit \(h \subset H, \, g \parallel H\)
Abstand der windschiefen Geraden \(g\) und \(h\) (vgl. Abiturskript - 2.4.4 Abstand Punkt - Ebene):
\(d(h;g) = d(B;H)\) mit \(g \subset H, \, h \parallel H\)
\[d(h;g) = \left| \overrightarrow{n}^{0}_{H} \circ (\overrightarrow{B} - \overrightarrow{A}) \right|\]
(Abstand der Geraden \(h\) von der Geraden \(g\))
\(d(g;h) = d(A;H)\) mit \(h \subset H, \, g \parallel H\)
\[d(h;g) = \left| \overrightarrow{n}^{0}_{H} \circ (\overrightarrow{A} - \overrightarrow{B}) \right|\]
(Abstand der Geraden \(g\) von der Geraden \(h\))
Dabei ist \(\overrightarrow{n}^{0}_{H}\) der Einheitsvektor des Normalenvektors \(\overrightarrow{n}_{H}\) der Hilfsebene \(H\) (vgl. 2.1.1 Rechnen mit Vektoren, Einheitsvektor).
Beispielaufgabe
Gegeben seien die Geraden \(g \colon \overrightarrow{X} = \begin{pmatrix} 2 \\ -6 \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}; \; \lambda \in \mathbb R\) und \(h \colon \overrightarrow{X} = \begin{pmatrix} 6 \\ -2 \\ 8 \end{pmatrix} + \mu \cdot \begin{pmatrix} -3 \\ 1 \\ 0 \end{pmatrix}; \; \mu \in \mathbb R\).
Zeigen Sie, dass \(g\) und \(h\) windschief sind und berechnen Sie den Abstand der beiden Geraden.
Nachweis, dass \(g\) und \(h\) windschief sind
Für die Untersuchung der gegenseitigen Lage der Geraden \(g\) und \(h\) werden die Richtungsvektoren der Geraden auf Lineare (Un-)Abhängigkeit hin überprüft (vgl. Abiturskript - 2.3.1 Lagebeziehung von Geraden).
\[g \colon \overrightarrow{X} = \begin{pmatrix} 2 \\ -6 \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}; \; \lambda \in \mathbb R\]
\[h \colon \overrightarrow{X} = \begin{pmatrix} 6 \\ -2 \\ 8 \end{pmatrix} + \mu \cdot \begin{pmatrix} -3 \\ 1 \\ 0 \end{pmatrix}; \; \mu \in \mathbb R\]
\[\begin{pmatrix} -3 \\ 1 \\ 0 \end{pmatrix} \neq k \cdot \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}; \; k \in \mathbb R\]
Die Richtungsvektoren der Geraden \(g\) und \(h\) sind linear unabhängig. Folglich können sich die Geraden in einem Punkt schneiden oder windschief zueinander verlaufen.
Prüfen, ob sich \(g\) und \(h\) in einem Punkt schneiden (vgl. Abiturskript - 2.3.1 Lagebeziehung von Geraden, Berechnung des Schnittpunkts zweier Geraden):
\[\begin{align*}\overrightarrow{X}_{g} &= \overrightarrow{X}_{h} \\[0.8em] \begin{pmatrix} 2 \\ -6 \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} &= \begin{pmatrix} 6 \\ -2 \\ 8 \end{pmatrix} + \mu \cdot \begin{pmatrix} -3 \\ 1 \\ 0 \end{pmatrix}\end{align*}\]
\[\begin{align*} \text{I} & & & \quad \enspace \;2 \hspace{30px} = \enspace \; \, 6 - 3\mu \\[0.8em] \text{II} & & \wedge & \enspace -6 + \lambda = -2 + \enspace \mu \\[0.8em] \text{III} & & \wedge & \quad \enspace \; 2 \hspace{30px} = \enspace \; 8 & & (\text{f})\end{align*}\]
Aufgrund des Widerspruchs in Gleichung III hat das lineare Gleichungssystem keine Lösung. Folglich verlaufen die Geraden \(g\) und \(h\) windschief zueinander.
Abstand der windschiefen Geraden \(g\) und \(h\)
\[g \colon \overrightarrow{X} = \begin{pmatrix} 2 \\ -6 \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}; \; \lambda \in \mathbb R\]
\[h \colon \overrightarrow{X} = \begin{pmatrix} 6 \\ -2 \\ 8 \end{pmatrix} + \mu \cdot \begin{pmatrix} -3 \\ 1 \\ 0 \end{pmatrix}; \; \mu \in \mathbb R\]
Hilfsebene \(H\) aufstellen, welche \(g\) enthält und zu \(h\) parallel ist:
\[g \subset H, \, h \parallel H\]
Normalenvektor \(\overrightarrow{n}_{H}\) der Hilfsebene \(H\):
Das Vektorprodukt der Richtungsvektoren \(\begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}\) und \(\begin{pmatrix} -3 \\ 1 \\ 0 \end{pmatrix}\) der Geraden \(g\) und \(h\) liefert einen Normalenvektor \(\overrightarrow{n}_{H}\) für die Ebenengleichung der Hilfsebene \(H\) in Normalenform (vgl. Abiturskript - 2.1.4 Vektorprodukt, Anwendungen des Vektorprodukts).
\[\begin{align*} \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} \times \begin{pmatrix} -3 \\ 1 \\ 0 \end{pmatrix} &= \begin{pmatrix} 1 & \cdot & 0 & - & 0 & \cdot & 1 \\ 0 & \cdot & (-3) & - & 0 & \cdot & 0 \\ 0 & \cdot & 1 & - & 1 & \cdot & (-3) \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 0 \\ 0 \\ 3 \end{pmatrix} \\[0.8em] &= 3 \cdot \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad \overrightarrow{n}_{H} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}\]
Aufpunkt der Hilfsebene \(H\): \((2|-6|2) \in g\)
\[\Longrightarrow \quad H \colon \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} 2 \\ -6 \\ 2 \end{pmatrix} \right] = 0\]
Oder in Koordinatendarstellung:
\[\begin{align*} \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} 2 \\ -6 \\ 2 \end{pmatrix} \right] &= 0 \\[0.8em] 0 \cdot (x_{1} - 2) + 0 \cdot (x_{2} - (-6)) + 1 \cdot (x_{3} - 2) &= 0 \\[0.8em] x_{3} - 2 &= 0 \end{align*}\]
\[\Longrightarrow \quad H \colon x_{3} - 2 = 0\]
Der Abstand \(d(h;g)\) der windschiefen Geraden \(g\) und \(h\) ist gleich dem Abstand des Aufpunktes \((6|-2|8) \in h\) von der Hilfsebene \(H\) (vgl. Abiturskript - 2.4.4 Abstand Punkt - Ebene).
Vektordarstellung:
\[\begin{align*} d(h;g) &= \frac{\left|\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \circ \left[ \begin{pmatrix} 6 \\ -2 \\ 8 \end{pmatrix} - \begin{pmatrix} 2 \\ -6 \\ 2 \end{pmatrix} \right] \right|}{\left| \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \right|} \\[0.8em] &= \frac{\left|\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \circ \begin{pmatrix} 4 \\ 4 \\ 6 \end{pmatrix} \right|}{\sqrt{0^{2} + 0^{2} + 1^{2}}} \\[0.8em] &= \frac{\vert 0 \cdot 4 + 0 \cdot 4 + 1 \cdot 6 \vert}{1} \\[0.8em] &= 6 \end{align*}\]
Koordinatendarstellung:
\[\begin{align*} d(h;g) &= \left| \frac{8 - 2}{\sqrt{0^{2} + 0^{2} + 1^{2}}} \right| \\[0.8em] &= 6 \end{align*}\]


