Abstand einer parallelen Gerade von einer Ebene
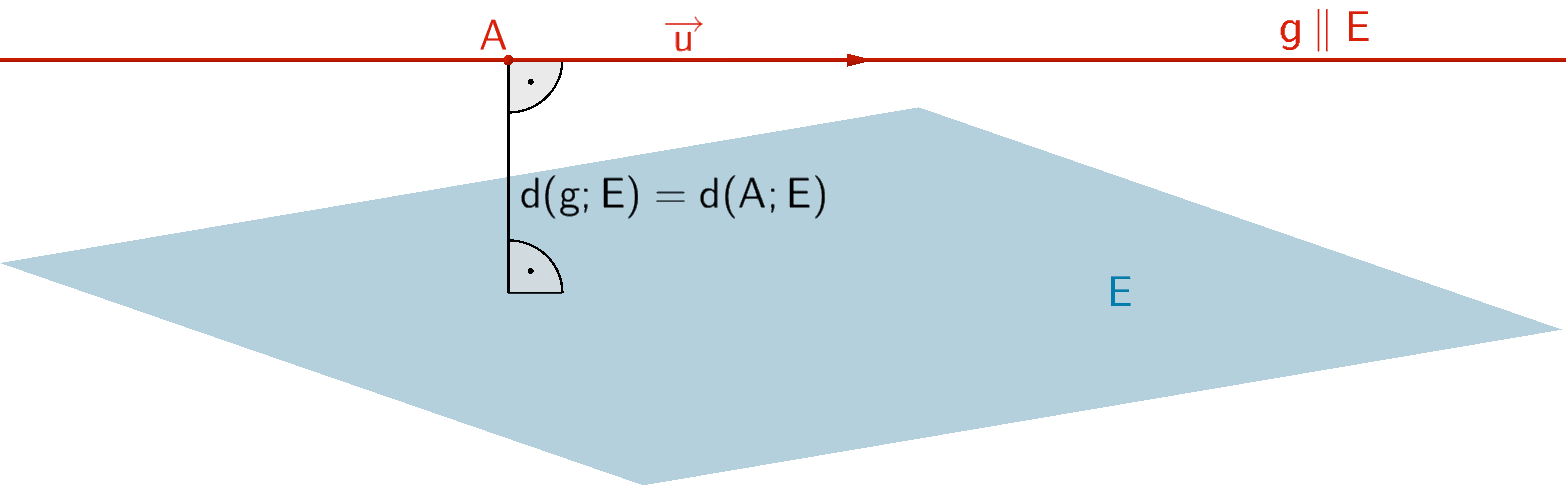
Die Abstandsbestimmung einer Gerade \(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}\,; \; \lambda \in \mathbb R\) von einer Ebene \(E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{B})\) mit \(g \parallel E\) lässt sich auf die Abstandsbestimmung eines beliebigen Punktes \(P \in g\) von der Ebene \(E\) zurückführen (vgl. Abiturskript - 2.4.4 Abstand Punkt - Ebene). Zweckmäßig wählt man den Aufpunkt \(A\) der Geradengleichung von \(g\).
\(d(g;E) = d(A;E)\) mit \(g \parallel E\)
Je nach Aufgabenstellung ist vorab der Abstandsbestimmung ggf. die Parallelität der Geraden \(g\) und der Ebene \(E\) nachzuweisen (vgl. Abiturskript - 2.3.2 Lagebeziehung von Gerade und Ebene).
Beispielaufgabe
Gegeben seien die Gerade \(g \colon \overrightarrow{X} = \begin{pmatrix} 2 \\ -2 \\ 2{,}5 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -1 \\ 4 \\ 2 \end{pmatrix}; \; \lambda \in \mathbb R\) sowie die Ebene \(E \colon -2x_{1} +2x_{2} -5x_{3} + 4 = 0\)
Weisen Sie nach, dass die Gerade \(g\) in konstantem Abstand zur Ebene \(E\) verläuft und berechnen Sie den Abstand \(d(g;E)\).
Nachweis, dass die Gerade \(g\) in konstantem Abstand zur Ebene \(E\) verläuft
Die Gerade \(g\) verläuft in konstante Abstand zur Ebene \(E\), wenn sie parallel zur Ebene \(E\) ist. Folglich muss das Skalarprodukt aus dem Richtungsvektor \(\overrightarrow{u}\) der Geradengleichung von \(g\) und dem Normalenvektor \(\overrightarrow{n}_{E}\) der Ebenengleichung von \(E\) gleich Null sein (vgl. Abiturskript - 2.1.3 Skalarprodukt von Vektoren, Anwendungen des Skalarprodukts).
\[g \colon \overrightarrow{X} = \begin{pmatrix} 2 \\ -2 \\ 2{,}5 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -1 \\ 4 \\ 2 \end{pmatrix}; \; \lambda \in \mathbb R \quad \Longrightarrow \quad \overrightarrow{u} = \begin{pmatrix} -1 \\ 4 \\ 2 \end{pmatrix}\]
\[E \colon -2x_{1} +2x_{2} -5x_{3} + 4 = 0 \quad \Longrightarrow \quad \overrightarrow{n}_{E} = \begin{pmatrix} -2 \\ 2 \\ -5 \end{pmatrix}\]
\[\overrightarrow{u} \circ \overrightarrow{n}_{E} = \begin{pmatrix} -1 \\ 4 \\ 2 \end{pmatrix} \circ \begin{pmatrix} -2 \\ 2 \\ -5 \end{pmatrix} = (-1) \cdot (-2) + 4 \cdot 2 + 2 \cdot (-5) = 0\]
\[\Longrightarrow \quad \overrightarrow{u} \perp \overrightarrow{n}_{E} \quad \Longrightarrow \quad g \parallel E\]
Abstand \(d(g;E)\) der Geraden \(g\) von der Ebene \(E\)
Der Abstand \(d(g;E)\) der Geraden \(g\) von der Ebenen \(E\) entspricht dem Abstand des Aufpunkts \((2|-2|2{,}5)\) der Geraden \(g\) von der Ebene \(E\) (vgl. Abiturskript - 2.4.4 Abstand Punkt - Ebene).
\[\overrightarrow{n}_{E} = \begin{pmatrix} -2 \\ 2 \\ -5 \end{pmatrix}\]
Gleichung der Ebene \(E\) in Hessescher Normalenform (vgl. Abiturskript - 2.2.3 Ebenengleichung in Normalenform, Hessesche Normalenform):
\[\begin{align*}&E \colon \frac{-2x_{1} +2x_{2} -5x_{3} + 4}{\sqrt{(-2)^{2} + 2^{2} + (-5)^{2}}} = 0 \\[0.8em] &E \colon \frac{-2x_{1} +2x_{2} -5x_{3} + 4}{\sqrt{33}} = 0 \end{align*}\]
Abstand \(d(g;E)\) berechnen:
\[\begin{align*} d(g;E) &= \left| \frac{(-2) \cdot 2 + 2 \cdot (-2) - 5 \cdot 2{,}5 + 4}{\sqrt{33}} \right| \\[0.8em] &= \left| \frac{-16{,}5}{\sqrt{33}} \right| \\[0.8em] &= \frac{\sqrt{33}}{2} \\[0.8em] &\approx 2{,}87 \end{align*}\]

