Abstand zweier parallelen Ebenen
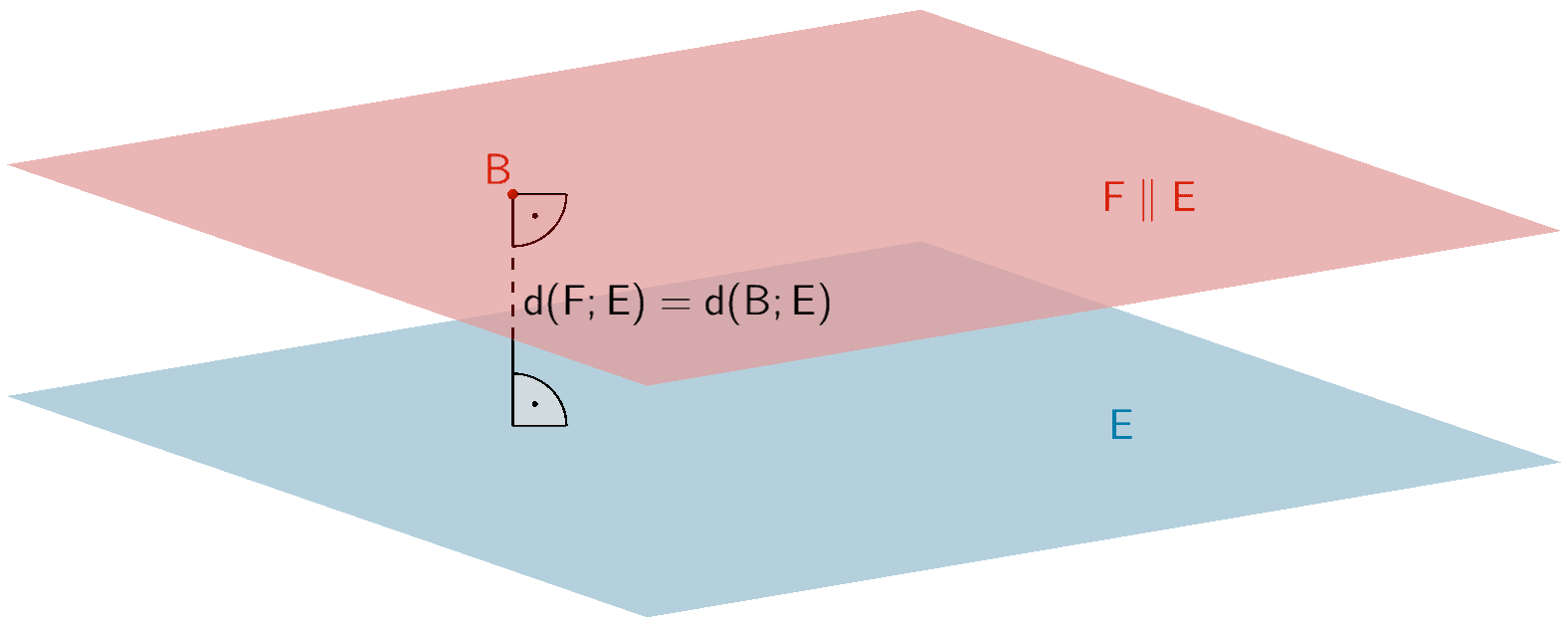
Die Abstandsbestimmung von zwei parallel zueinander liegenden Ebenen \(E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A})\) und \(F \colon \overrightarrow{n}_{F} \circ (\overrightarrow{X} - \overrightarrow{B})\) lässt sich auf die Abstandsbestimmung eines beliebigen Punktes \(P \in F\) von der Ebene \(E\) zurückführen (vgl. Abiturskript - 2.4.4 Abstand Punkt - Ebene). Zweckmäßig wählt man den Aufpunkt \(B\) der Ebenengleichung von \(F\).
\(d(F;E) = d(B;E)\) mit \(F \parallel E\)
Je nach Aufgabenstellung ist vorab der Abstandsbestimmung ggf. die Parallelität der Ebenen \(E\) und \(F\) nachzuweisen (vgl. Abiturskript - 2.3.3 Lagebeziehung von Ebenen).
Beispielaufgabe
Die Grundfläche \(ABC\) der Pyramiden \(ABCS\) liegt in der Ebene \(E \colon -x_{1} - x_{2} + 6x_{3} = 0\). Die Spitzen \(S\) der Pyramiden \(ABCS\) liegen in der Ebene \(F \colon \overrightarrow{X} = \begin{pmatrix} 3 \\ 9 \\ 8 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 3 \\ 9 \\ 2 \end{pmatrix} + \mu \cdot \begin{pmatrix} 3 \\ 3 \\ 1 \end{pmatrix}; \; \lambda, \mu \in \mathbb R\).
Weisen Sie nach, dass die Pyramiden \(ABCS\) volumengleich sind und berechnen Sie die Höhe \(h\) der Pyramiden \(ABCS\).
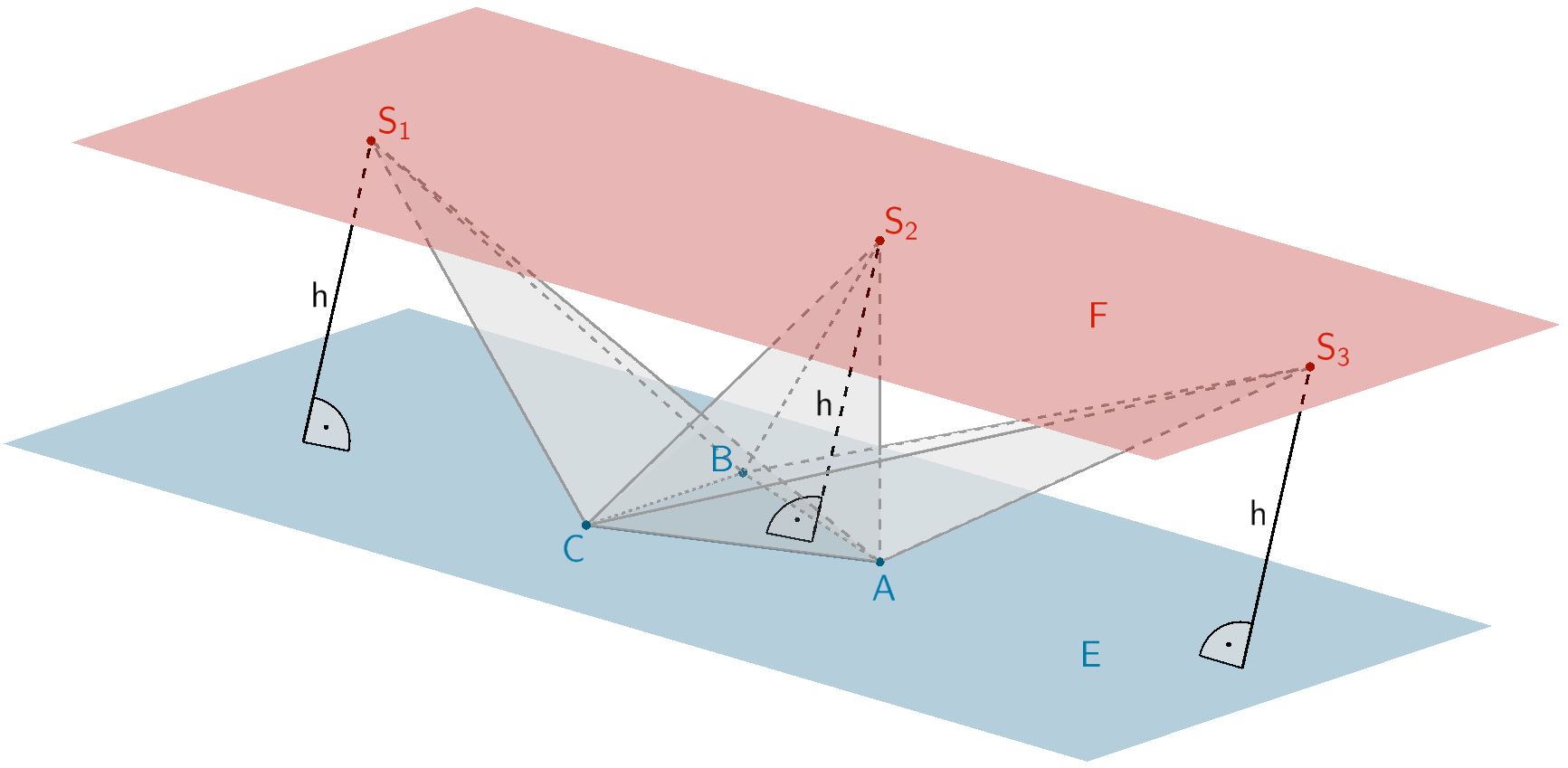
Pyramiden \(ABCS\) mit der Grundfläche \(ABC \subset E\), den Spitzen \(S \in F\) und der Höhe \(h\)
\[V_{ABCS} = \frac{1}{3} \cdot A_{ABC} \cdot h\]
Bei gleicher Grundfläche \(ABC\) hängt der Volumeninhalt \(V_{ABCS}\) der Pyramiden \(ABCS\) nur von der Höhe \(h\) ab. Für volumengleiche Pyramiden \(ABCS\) muss die Höhe \(h\) demnach einen konstanten Wert annehmen. Dies ist dann der Fall, wenn die Spitzen \(S \in F\) in einer Ebene \(F\) liegen, welche im Abstand \(h = d(F;E)\) parallel zur Ebene \(E\) ist. Folglich ist die Parallelität der Ebenen \(E\) und \(F\) nachzuweisen und deren Abstand zu berechnen.
Nachweis der Parallelität der Ebenen \(E\) und \(F\)
\[E \colon -x_{1} - x_{2} + 6x_{3} = 0\]
\[F \colon \overrightarrow{X} = \begin{pmatrix} 3 \\ 9 \\ 8 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 3 \\ 9 \\ 2 \end{pmatrix} + \mu \cdot \begin{pmatrix} 3 \\ 3 \\ 1 \end{pmatrix}; \; \lambda, \mu \in \mathbb R\]
Für den Nachweis der Parallelität der Ebenen \(E\) und \(F\) betrachtet man entweder das Skalarprodukt aus dem Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\) und jeweils einem der Richtungsvektoren \(\overrightarrow{u}\) und \(v\) der Gleichung der Ebene \(F\) oder die Lineare (Un-)Abhängigkeit der Normalenvektoren \(\overrightarrow{n}_{E}\) und \(\overrightarrow{n}_{F}\) der Ebenen \(E\) und \(F\) (vgl. Abiturskript - 2.3.3 Lagebeziehung von Ebenen). Den Normalenvektor \(\overrightarrow{n}_{F}\) liefert das Vektorprodukt \(\overrightarrow{u} \times \overrightarrow{v}\) (vgl. Abiturskript - 2.1.4 Vektorprodukt, Anwendungen des Vektorprodukts). Um die Identität der Ebenen \(E\) und \(F\) auszuschließen, weist man beispielsweise nach, dass der Aufpunkt \((3|9|8)\) der Ebenengleichung von \(F\) nicht die Ebenengleichung von \(E\) erfüllt.
Für die Parallelität der Ebenen \(E\) und \(F\) muss also wahlweise gelten:
\[\overrightarrow{n_{E}} \circ \overrightarrow{u} = 0 \quad \Longleftrightarrow \quad \overrightarrow{n}_{E} \perp \overrightarrow{u}\]
und
\[\overrightarrow{n_{E}} \circ \overrightarrow{v} = 0 \quad \Longleftrightarrow \quad \overrightarrow{n}_{E} \perp \overrightarrow{v}\]
und
\[(3|9|8) \notin E\]
\[\Longrightarrow \quad F \parallel E\]
\[\overrightarrow{n}_{E} = k \cdot \overrightarrow{n}_{F}\,; \; k \in \mathbb R\]
bzw.
\[\overrightarrow{n}_{F} = k \cdot \overrightarrow{n}_{E}\,; \; k \in \mathbb R\]
und
\[(3|9|8) \notin E\]
\[\Longrightarrow \quad F \parallel E\]
1. Möglichkeit: Normalenvektor von \(E\) und Richtungsvektoren von \(F\) betrachten
\[E \colon -x_{1} - x_{2} + 6x_{3} = 0 \quad \Longrightarrow \quad \overrightarrow{n}_{E} = \begin{pmatrix} -1 \\ -1 \\ 6 \end{pmatrix}\]
\[F \colon \overrightarrow{X} = \begin{pmatrix} 3 \\ 9 \\ 8 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 3 \\ 9 \\ 2 \end{pmatrix} + \mu \cdot \begin{pmatrix} 3 \\ 3 \\ 1 \end{pmatrix}; \; \lambda, \mu \in \mathbb R\]
\[\Longrightarrow \quad \overrightarrow{u} = \begin{pmatrix} 3 \\ 9 \\ 2 \end{pmatrix}; \; \overrightarrow{v} = \begin{pmatrix} 3 \\ 3 \\ 1 \end{pmatrix}\]
Orthogonalität \(\overrightarrow{n}_{E} \perp \overrightarrow{u}\) und \(\overrightarrow{n}_{E} \perp \overrightarrow{v}\) prüfen (vgl. Abiturskript - 2.1.3 Skalarprodukt von Vektoren, Anwendungen des Skalarprodukts):
\[\begin{align*}\overrightarrow{n}_{E} \circ \overrightarrow{u} &= \begin{pmatrix} -1 \\ -1 \\ 6 \end{pmatrix} \circ \begin{pmatrix} 3 \\ 9 \\ 2 \end{pmatrix} \\[0.8em] &= (-1) \cdot 3 + (-1) \cdot 9 + 6 \cdot 2 \\[0.8em] &= 0\end{align*}\]
\[\Longrightarrow \quad \overrightarrow{n}_{E} \perp \overrightarrow{u}\]
\[\begin{align*}\overrightarrow{n}_{E} \circ \overrightarrow{v} &= \begin{pmatrix} -1 \\ -1 \\ 6 \end{pmatrix} \circ \begin{pmatrix} 3 \\ 3 \\ 1 \end{pmatrix} \\[0.8em] &= (-1) \cdot 3 + (-1) \cdot 3 + 6 \cdot 1 \\[0.8em] &= 0\end{align*}\]
\[\Longrightarrow \quad \overrightarrow{n}_{E} \perp \overrightarrow{v}\]
Identität der Ebenen \(E\) und \(F\) ausschließen:
Aufpunkt \((3|9|8) \in F\)
\[E \colon -x_{1} - x_{2} + 6x_{3} = 0\]
Punktprobe in \(E\,\):
\[\begin{align*} -3 - 9 + 6 \cdot 8 &= 0 \\[0.8em] 36 &= 0 \quad (\text{f}) \end{align*}\]
\[\Longrightarrow \quad (3|9|8) \notin E\]
\[\Longrightarrow \quad F \parallel E\]
\(\Longrightarrow \quad\)Die Pyramiden \(ABCS\) sind volumengleich.
2. Möglichkeit: Normalenvektoren von \(E\) und \(F\) betrachten
\[E \colon -x_{1} - x_{2} + 6x_{3} = 0 \quad \Longrightarrow \quad \overrightarrow{n}_{E} = \begin{pmatrix} -1 \\ -1 \\ 6 \end{pmatrix}\]
\[F \colon \overrightarrow{X} = \begin{pmatrix} 3 \\ 9 \\ 8 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 3 \\ 9 \\ 2 \end{pmatrix} + \mu \cdot \begin{pmatrix} 3 \\ 3 \\ 1 \end{pmatrix}; \; \lambda, \mu \in \mathbb R\]
\[\Longrightarrow \quad \overrightarrow{u} = \begin{pmatrix} 3 \\ 9 \\ 2 \end{pmatrix}; \; \overrightarrow{v} = \begin{pmatrix} 3 \\ 3 \\ 1 \end{pmatrix}\]
Normalenvektor \(\overrightarrow{n}_{F}\) der Ebene \(F\) bestimmen:
\[\begin{align*} \overrightarrow{u} \times \overrightarrow{v} &= \begin{pmatrix} 3 \\ 9 \\ 2 \end{pmatrix} \times \begin{pmatrix} 3 \\ 3 \\ 1 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 9 & \cdot & 1 & - & 2 & \cdot & 3 \\ 2 & \cdot & 3 & - & 3 & \cdot & 1 \\ 3 & \cdot & 3 & - & 9 & \cdot & 3 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 3 \\ 3 \\ -18 \end{pmatrix} \\[0.8em] &= 3 \cdot \begin{pmatrix} 1 \\ 1 \\ -6 \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad \overrightarrow{n}_{F} = \begin{pmatrix} 1 \\ 1 \\ -6 \end{pmatrix}\]
Lineare (Un-)Abhängigkeit der Normalenvektoren \(\overrightarrow{n}_{E}\) und \(\overrightarrow{n}_{F}\) prüfen (vgl. Abiturskript - 2.1.2 Lineare (Un-)Abhängigkeit von Vektoren):
\[\begin{align*}\overrightarrow{n}_{F} &= k \cdot \overrightarrow{n}_{E}\,; \; k \in \mathbb R \\[0.8em] \begin{pmatrix} 1 \\ 1 \\ -6 \end{pmatrix} &= (-1) \cdot \begin{pmatrix} -1 \\ -1 \\ 6 \end{pmatrix} \end{align*}\]
\(\Longrightarrow \quad\)\(\overrightarrow{n}_{E}\) und \(\overrightarrow{n}_{F}\) sind linear abhängig.
Folglich können die Ebenen \(E\) und \(F\) identisch sein oder (echt) parallel zueinander liegen.
Identität der Ebenen \(E\) und \(F\) ausschließen:
Aufpunkt \((3|9|8) \in F\)
\[E \colon -x_{1} - x_{2} + 6x_{3} = 0\]
Punktprobe in \(E\,\):
\[\begin{align*} -3 - 9 + 6 \cdot 8 &= 0 \\[0.8em] 36 &= 0 \quad (\text{f}) \end{align*}\]
\[\Longrightarrow \quad (3|9|8) \notin E\]
\[\Longrightarrow \quad F \parallel E\]
\(\Longrightarrow \quad\)Die Pyramiden \(ABCS\) sind volumengleich.
Höhen \(h\) der Pyramiden \(ABCS\)
Die Höhe \(h\) der Pyramiden \(ABCS\) ist gleich dem Abstand \(d(F;E)\) der parallelen Ebenen \(E\) und \(F\). Die Abstandsbestimmung der Ebenen lässt sich auf den Abstand des Auspunkte \((3|9|8)\) der Gleichung der Ebene \(F\) von der Ebene \(E\) zurückführen.
\[E \colon -x_{1} - x_{2} + 6x_{3} = 0 \quad \Longrightarrow \quad \overrightarrow{n}_{E} = \begin{pmatrix} -1 \\ -1 \\ 6 \end{pmatrix}\]
Aufpunkt \((3|9|8) \in F\)
Gleichung der Ebene \(E\) in Hessescher Normalenform (vgl. Abiturskript - 2.2.3 Ebenengleichung in Normalenform, Hessesche Normalenform):
\[\begin{align*}&E \colon \frac{-x_{1} - x_{2} + 6x_{3}}{\sqrt{(-1)^{2} + (-1)^{2} + 6^{2}}} = 0 \\[0.8em] &E \colon \frac{-x_{1} - x_{2} + 6x_{3}}{\sqrt{38}} = 0 \end{align*}\]
Höhe \(h\) der Pyramiden \(ABCS\) berechnen:
\[\begin{align*} h &= d(F;E) \\[0.8em] &= \left| \frac{-3 - 9 + 6 \cdot 8}{\sqrt{38}} \right| \\[0.8em] &= \frac{36}{\sqrt{38}} \\[0.8em] &= \frac{18\sqrt{38}}{19} \\[0.8em] &\approx 5{,}84 \end{align*}\]

