Schnittwinkel zwischen Gerade und Ebene
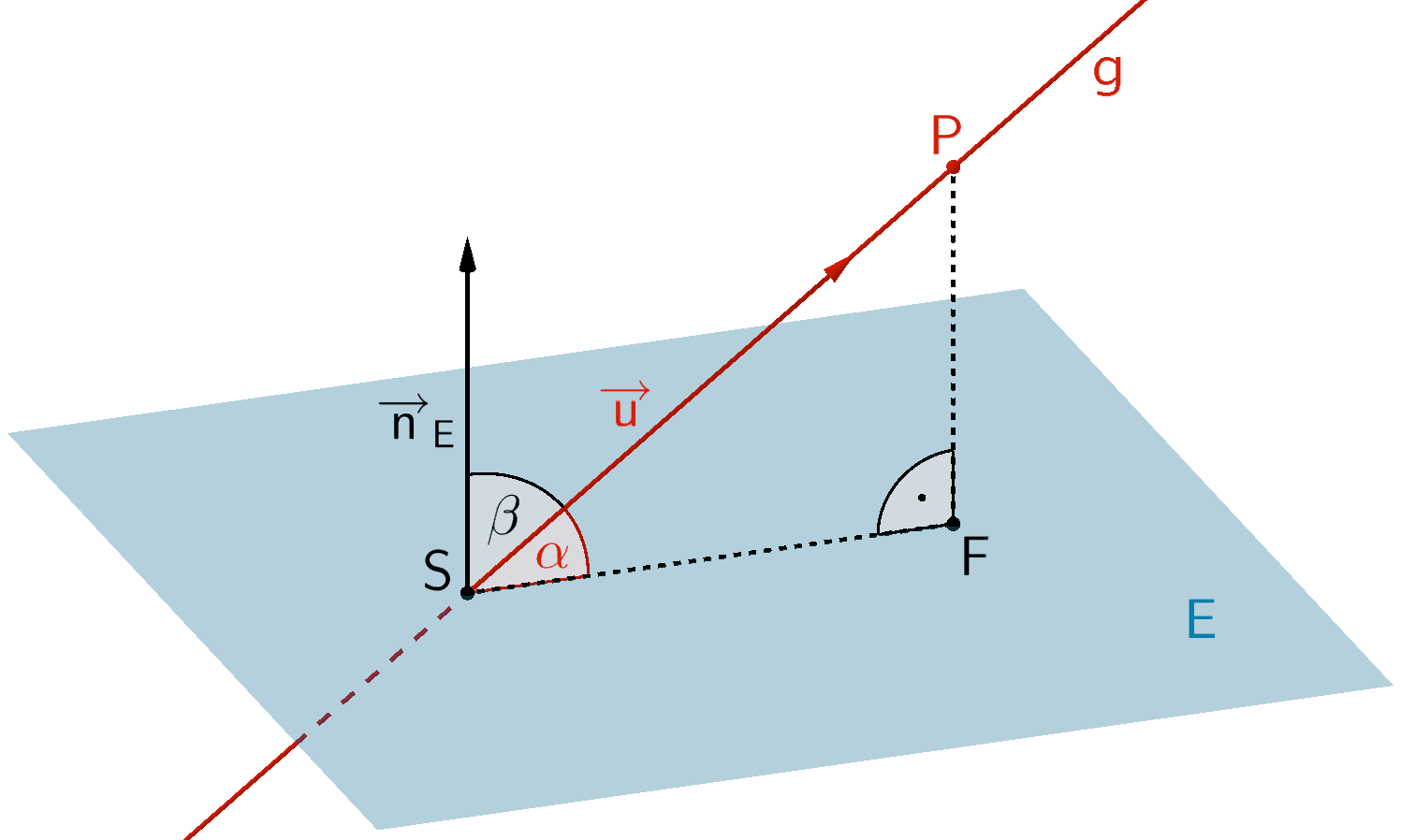
Unter dem Schnittwinkel zwischen einer Geraden \(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}\,; \; \lambda \in \mathbb R\) und einer Ebene \(E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{B})\) versteht man den Winkel \(\measuredangle FSP\) im rechtwinkligen Dreieck \(SFP\). Dabei ist \(S\) der Schnittpunkt der Geraden \(g\) mit der Ebene \(E\), \(P\) ein beliebiger Punkt der Geraden \(g\) und \(F\) der Lotfußpunkt des Lotes von \(P\) auf die Ebene \(E\).
Man erhält den Schnittwinkel \(\alpha\), indem man zunächst den spitzen Winkel \(\beta\) berechnet, den der Richtungsvektor \(\overrightarrow{u}\) der Geraden \(g\) und der Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\) einschließt. Der Schnittwinkel \(\alpha\) ergibt sich zu \(\alpha = 90^{\circ} - \beta\).
Andererseits gilt die Komplementwinkelbeziehung \(\cos \beta = \cos(90^{\circ} - \alpha) = \sin \alpha\).
Schnittwinkel \(\boldsymbol{\alpha}\) zwischen Gerade und Ebene
\[\begin{align*} \cos \beta &= \frac{\vert \overrightarrow{u} \circ \overrightarrow{n}_{E} \vert}{\vert \overrightarrow{u} \vert \cdot \vert \overrightarrow{n}_{E} \vert} & & (0^{\circ} \leq \beta \leq 90^{\circ}) \\[0.8em] \alpha &= 90^{\circ} - \beta & & (0^{\circ} \leq \alpha \leq 90^{\circ}) \end{align*}\]
oder
\[\sin \alpha = \frac{\vert \overrightarrow{u} \circ \overrightarrow{n}_{E} \vert}{\vert \overrightarrow{u} \vert \cdot \vert \overrightarrow{n}_{E} \vert} \qquad (0^{\circ} \leq \alpha \leq 90^{\circ})\]
Je nach Aufgabenstellung ist vorab der Berechnung des Schnittwinkels zwischen einer Geraden und einer Ebene nachzuweisen, dass die Gerade und die Ebene sich schneiden (vgl. Abiturskript - 2.3.2 Lagebeziehung von Gerade und Ebene).
Beispielaufgabe
Gegeben sei die Gerade \(g \colon \overrightarrow{X} = \begin{pmatrix} -1 \\ -2 \\ 0 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 5 \\ 6 \\ 6 \end{pmatrix}\,; \; \lambda \in \mathbb R\) sowie die Ebene \(E \colon \overrightarrow{X} = \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} + \tau \cdot \begin{pmatrix} 1 \\ -2 \\ -1 \end{pmatrix} + \sigma \cdot \begin{pmatrix} 2 \\ 4 \\ 1 \end{pmatrix}\,; \; \tau, \sigma \in \mathbb R\).
Berechnen Sie den Schnittwinkel \(\alpha\) zwischen der Geraden \(g\) und der Ebene \(E\).
\[g \colon \overrightarrow{X} = \begin{pmatrix} -1 \\ -2 \\ 0 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 5 \\ 6 \\ 6 \end{pmatrix}\,; \; \lambda \in \mathbb R \quad \Longrightarrow \quad \overrightarrow{u} = \begin{pmatrix} 5 \\ 6 \\ 6 \end{pmatrix}\]
\[E \colon \overrightarrow{X} = \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} + \tau \cdot \begin{pmatrix} 1 \\ -2 \\ -1 \end{pmatrix} + \sigma \cdot \begin{pmatrix} 2 \\ 4 \\ 1 \end{pmatrix}\,; \; \tau, \sigma \in \mathbb R\]
\[\Longrightarrow \quad \overrightarrow{v} = \begin{pmatrix} 1 \\ -2 \\ -1 \end{pmatrix}; \; \overrightarrow{w} = \begin{pmatrix} 2 \\ 4 \\ 1 \end{pmatrix}\]
Da die Gleichung der Ebene \(E\) in der Parameterform vorliegt, wird zunächst mithilfe des Vektorprodukts der Richtungsvektoren \(\overrightarrow{v}\) und \(\overrightarrow{w}\) ein Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\) ermittelt (vgl. Abiturskript - 2.1.4 Vektorprodukt, Anwendungen des Vektorprodukts).
\[\begin{align*} \overrightarrow{v} \times \overrightarrow{w} &= \begin{pmatrix} 1 \\ -2 \\ -1 \end{pmatrix} \times \begin{pmatrix} 2 \\ 4 \\ 1 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} (-2) & \cdot & 1 & - & (-1) & \cdot & 4 \\ (-1) & \cdot & 2 & - & 1 & \cdot & 1 \\ 1 & \cdot & 4 & - & (-2) & \cdot & 2 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 2 \\ -3 \\ 8 \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad \overrightarrow{n}_{E} = \begin{pmatrix} 2 \\ -3 \\ 8 \end{pmatrix}\]
Schnittwinkel \(\alpha\) berechnen:
\[\overrightarrow{u} = \begin{pmatrix} 5 \\ 6 \\ 6 \end{pmatrix}; \; \overrightarrow{n}_{E} = \begin{pmatrix} 2 \\ -3 \\ 8 \end{pmatrix}\]
\[\begin{align*}\cos \beta &= \frac{\vert \overrightarrow{u} \circ \overrightarrow{n}_{E} \vert}{\vert \overrightarrow{u} \vert \cdot \vert \overrightarrow{n}_{E} \vert} \\[0.8em] &= \frac{\left| \begin{pmatrix} 5 \\ 6 \\ 6 \end{pmatrix} \circ \begin{pmatrix} 2 \\ -3 \\ 8 \end{pmatrix} \right| }{\left| \begin{pmatrix} 5 \\ 6 \\ 6 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 2 \\ -3 \\ 8 \end{pmatrix} \right|} \\[0.8em] &= \frac{\vert 5 \cdot 2 + 6 \cdot (-3) + 6 \cdot 8 \vert}{\sqrt{5^{2} + 6^{2} + 6^{2}} \cdot \sqrt{2^{2} + (-3)^{2} + 8^{2}}} \\[0.8em] &= \frac{40}{\sqrt{97} \cdot \sqrt{77}} \qquad | \; \text{TR:} \; \cos^{-1} \left( \frac{40}{\sqrt{97} \cdot \sqrt{77}}\right) \\[3.2em] \beta &\approx 62{,}43^{\circ} \end{align*}\]
\[\alpha \approx 90^{\circ} - 62{,}43^{\circ} = 27{,}57^{\circ}\]
oder
\[\begin{align*}\sin \alpha &= \frac{\vert \overrightarrow{u} \circ \overrightarrow{n}_{E} \vert}{\vert \overrightarrow{u} \vert \cdot \vert \overrightarrow{n}_{E} \vert} \\[0.8em] &= \frac{\left| \begin{pmatrix} 5 \\ 6 \\ 6 \end{pmatrix} \circ \begin{pmatrix} 2 \\ -3 \\ 8 \end{pmatrix} \right| }{\left| \begin{pmatrix} 5 \\ 6 \\ 6 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 2 \\ -3 \\ 8 \end{pmatrix} \right|} \\[0.8em] &= \frac{\vert 5 \cdot 2 + 6 \cdot (-3) + 6 \cdot 8 \vert}{\sqrt{5^{2} + 6^{2} + 6^{2}} \cdot \sqrt{2^{2} + (-3)^{2} + 8^{2}}} \\[0.8em] &= \frac{40}{\sqrt{97} \cdot \sqrt{77}} \qquad | \; \text{TR:} \; \sin^{-1}\left( \dfrac{40}{\sqrt{97} \cdot \sqrt{77}} \right) \\[3.2em] \alpha &\approx 27{,}57^{\circ} \end{align*}\]

