Ergebnisraum und Ereignisse
Ergebnis
Die Versuchsausgänge von Zufallsexperimenten werden als Ergebnisse \(\omega\) bezeichnet.
Ergebnisraum
Die Menge aller Ergebnisse \(\omega\) bildet den Ergebnisraum \(\Omega\), wobei jedes mögliche Ergebnis genau einmal in \(\Omega\) vorkommt.
Mächtigkeit des Ergebnisraums
Die Anzahl der Elemente des Ergebnisraums \(\Omega\) wird als Mächtigkeit \(\vert \Omega \vert\) des Ergebnisraums bezeichnet
Ereignis
Jede Teilmenge \(E\) des Ergebnisraums \(\Omega\) beschreibt ein Ereignis. Ein Ereignis \(E\) tritt ein, wenn ein Versuchsergebnis \(\omega\) ein Element der Menge \(E\) ist. Ereignisse können als Menge \(E = \{\omega_{1}, \omega_{2}, ...\}\) oder in sprachlicher Form \(E \colon „\text{Beschreibung des Ereignisses}"\) angegeben werden.
Mächtigkeit eines Ereignisses
Die Anzahl der Elemente eines Ereignisses \(E\) wird als Mächtigkeit \(\vert E \vert\) des Ereignisses bezeichnet.
Elementarereignis
Ein Ereignis, das nur ein Versuchsergebnis enthält, wird als Elementarereignis bezeichnet.
Unmögliches Ereignis
Das unmögliche Ereignis \(\{\,\}\) (leere Menge, auch: \(\varnothing\)), enthält kein Ergebnis und tritt nie ein.
Sicheres Ereignis
Das sichere Ereignis \(\Omega\) tritt immer ein.
Verknüpfung von Ereignissen
Durch die Verknüpfung von einzelnen Ereignissen \(E_{1}, E_{2}, ...\), beispielsweise durch Bildung der Schnittmenge \(E_{1} \cap E_{2}\) oder der Vereinigungsmenge \(E_{1} \cup E_{2}\), entstehen neue Ereignisse, die wiederum Teilmengen des Ergenisraums \(\Omega\) sind.
Die folgende Tabelle gibt ausgehend von zwei Ereignissen \(A\) und \(B\) einen Überblick über die Verknüpfung von Ereignissen.
|
Symbolschreibweise und Sprechweise
|
Veranschaulichung als Mengendiagramm
|
||
|
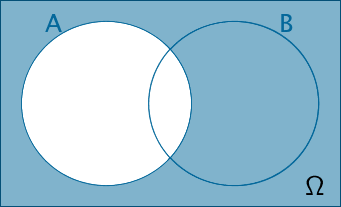
\(\overline{A} = \Omega \backslash A\)
Gegenereignis zu \(A\);
Nicht das Ereignis \(A\)
|
 |
||
|
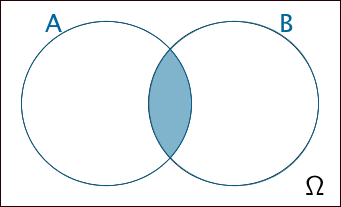
\(A \cap B\)
Schnittmenge
Ereignis \(A\) und Ereignis \(B\);
Beide Ereignisse zugleich;
Sowohl \(A\) als auch \(B\)
|
 |
||
|
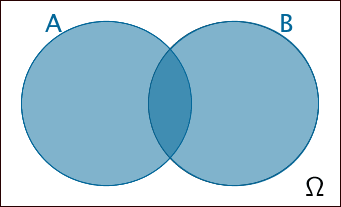
\(A \cup B = (A \cap \overline{B}) \cup (B \cap \overline{A}) \cup (A \cap B)\)
Vereinigungsmenge
Ereignis \(A\) oder Ereignis \(B\) oder beide zugleich;
Mindestens eines der beiden Ereignisse
|
 |
||
|
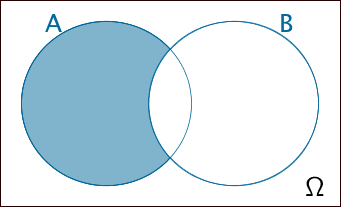
\(A \cap \overline{B} = A \backslash B\)
Ereignis \(A\) und nicht Ereignis \(B\);
Ereignis \(A\) ohne Ereignis \(B\)
|
 |
||
|
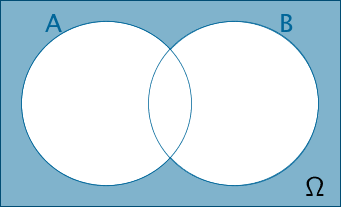
\(\overline{A} \cap \overline{B} = \overline{A \cup B}\)
Weder Ereignis \(A\) noch Ereignis \(B\);
Keines der beiden Ereignisse
|
 |
||
|
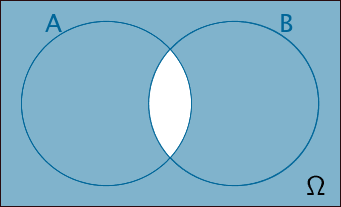
\(\overline{A \cap B} = \overline{A} \cup \overline{B}\)
Nicht beide Ereignisse zugleich;
Höchstens eines der beiden Ereignisse
|
 |
||
|
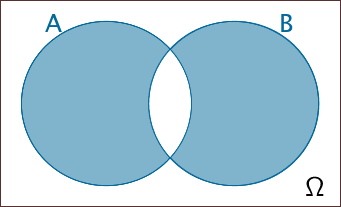
\((A \cap \overline{B}) \cup (B \cap \overline{A}) = A \backslash B \cup B \backslash A\)
Entweder Ereignis \(A\) oder Ereignis \(B\);
Genau eines der beiden Ereignisse
|
 |
Gesetze der Ereignisalgebra
Es gelten folgende Gesetze der Ereignisalgebra (Auszug):
| Kommutativgesetz |
\(A \cap B = B \cap A\)
\(A \cup B = B \cup A\)
|
| Assoziativgesetz |
\((A \cap B) \cap C = A \cap (B \cap C)\)
\((A \cup B) \cup C = A \cup (B \cup C)\)
|
| Distributivgesetz |
\(A \cap (B \cup C) = (A \cap B) \cup (A \cap C)\)
\(A \cup (B \cap C) = (A \cup B) \cap (A \cup C)\)
|
| De-Morgan-Gesetze |
\(\overline{A} \cap \overline{B} = \overline{A \cup B}\)
\(\overline{A} \cup \overline{B} = \overline{A \cap B}\)
|
| Komplemente |
\(A \cap \overline{A} = \varnothing\)
\(A \cup \overline{A} = \Omega\)
\(\overline{\overline{A}} = A\)
|
Beispielaufgabe
Ein Markforschungsinstitut untersucht das Konsumverhalten der Bevölkerung Deutschlands hinsichtlich der Kaufabsicht eines Tablets. Bei einer Befragung von Passanten in der Fußgängerzone einer Großstadt werden unter anderem folgende Ereignisse berücksichtigt:
\(S\): „Die befragte Person ist über 60 Jahre alt."
\(T\): „Die befragte Person beabsichtigt den Kauf eines Tablets."
Beschreiben Sie die folgenden Ereignisse im Sachzusammenhang.
a) \((\overline{S} \cap T) \cup (\overline{T} \cap S)\)
b) \(\overline{\overline{S} \cap T}\)
c) \(\overline{S \cup \overline{T}}\)
a) Ereignis \((\overline{S} \cap T) \cup (\overline{T} \cap S)\)
\(\overline{S} \cap T = T \backslash S\):
„Die befragte Person ist unter 60 Jahre alt und beabsichtigt den Kauf eines Tablets."
\(\overline{T} \cap S = S \backslash T\):
„Die befragte Person ist über 60 Jahre alt und beabsichtigt nicht den Kauf eines Tablets."
\((\overline{S} \cap T) \cup (\overline{T} \cap S) = T \backslash S \cup S \backslash T\):
„Die befragte Person ist entweder unter 60 Jahre alt und beabsichtigt den Kauf eines Tablets oder sie ist über 60 Jahre alt und beabsichtigt nicht den Kauf eines Tablets."
b) Ereignis \(\overline{\overline{S} \cap T}\)
Gesetz von De Morgan anwenden:
\(\overline{\overline{S} \cap T} = S \cup \overline{T}\):
„Die befragt Person ist über 60 Jahre alt oder beabsichtigt den Kauf eines Tablets (oder beides zugleich)."
c) Ereignis \(\overline{S \cup \overline{T}}\)
Gesetz von De Morgan anwenden:
\(\overline{S \cup \overline{T}} = \overline{S} \cap T\):
„Die befragte Person ist unter 60 Jahre alt und beabsichtigt den Kauf eines Tablets."


