Baumdiagramm
Bei der Bestimmung der Wahrscheinlichkeiten von mehrstufigen bzw. zusammengesetzten Zufallsexperimenten sind Baumdiagramme ein äußerst anschauliches Hilfsmittel.
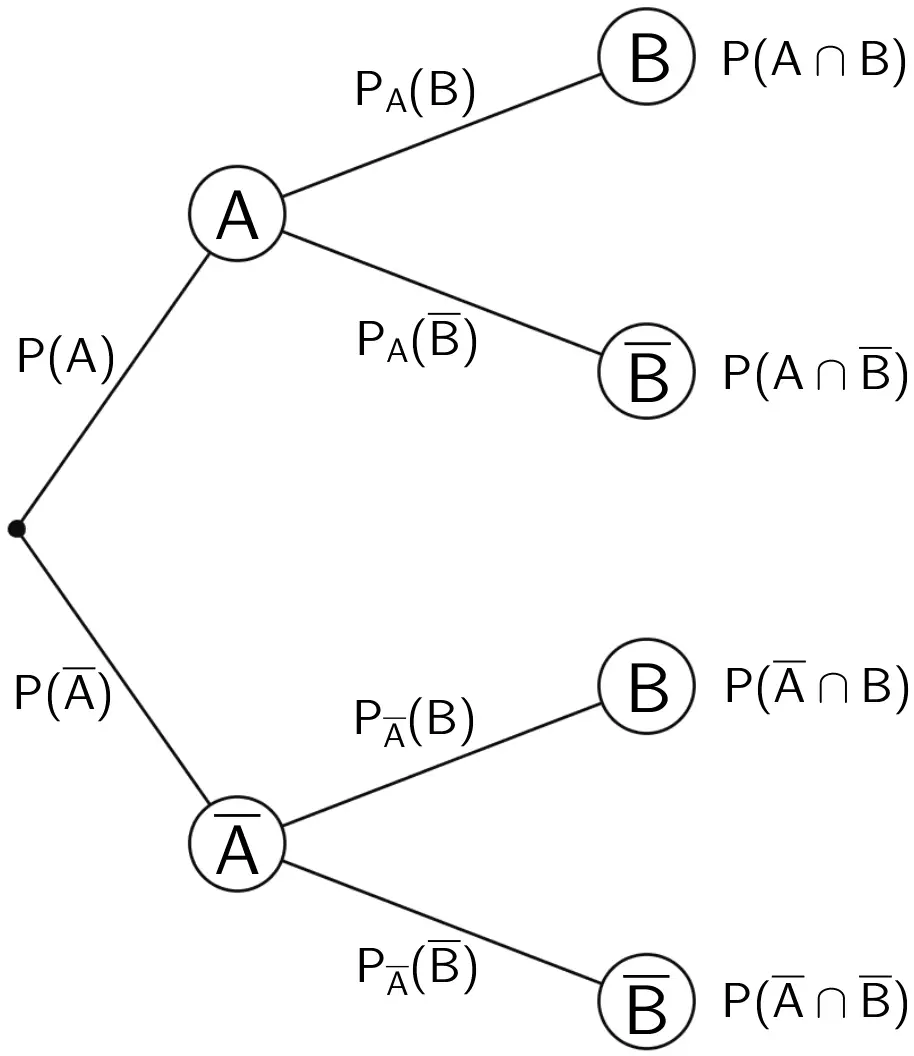
Baumdiagramm für ein zweistufiges Zufallsexperiment
Die Wahrscheinlichkeiten der Ereignisse werden an den Pfaden angetragen, die zu den Ereignissen führen. Dabei ist zu beachten, dass ab der zweiten Stufe eines mehrstufigen Zufallsexperiments alle Ereignisse vom Ausgang der vorangegangenen Stufe abhängen. Deshalb sind ab der zweiten Stufe die bedingten Wahrscheinlichkeiten an den Pfaden eines Baumdiagramms zu notieren (vgl. Abiturskript - 3.1.5 Bedingte Wahrscheinlichkeit).
Ausnahme: Stochastische Unabhängigkeit der Ereignisse (vgl. Abiturskript - 3.1.6 Unabhängigkeit von Ereignissen).
An den Enden eines Baumdiagramms lassen sich die Wahrscheinlichkeiten für das gleichzeitige Eintreten der Ereignisse (Schnittmengen) antragen.
Für die Bestimmung der Wahrscheinlichkeiten eines mehrstufigen Zufallsexperiments mithilfe eines Baumdiagramms gelten folgende Pfadregeln:
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
Beispiel:
Auf Wunsch der Mitarbeiter veranstaltet eine Firma einen sportlichen Betriebsausflug. Alle Mitarbeiter nehmen daran teil. Die Mitarbeiter können zwischen einer Wanderung und einem Fahrradausflug wählen. Außerdem besteht die Möglichkeit, sich jeweils für eine kürzere oder eine längere Strecke zu entscheiden. 60 % der Mitarbeiter entscheiden sich für eine Wanderung. Davon wählen 30 % die kürzere Strecke. 10 % aller Mitarbeiter nehmen an dem Fahrradausflug teil und wählen die längere Strecke.
Fertigen Sie ein vollständig beschriftetes Baumdiagramm an und berechnen Sie die Wahrscheinlichkeit dafür, dass ein beliebiger Mitarbeiter eine kürzere Strecke wählt.
Die Ereignisse können beispielsweise wie folgt festgelegt werden:
\(W\): „Ein Mitarbeiter entscheidet sich für die Wanderung."
\(\overline{W}\): „Ein Mitarbeiter entscheidet sich für den Fahrradausflug."
\(K\): „Ein Mitarbeiter entscheidet sich für die kürzere Strecke."
\(\overline{K}\): „Ein Mitarbeiter entscheidet sich für die längere Strecke."
Vollständig beschriftetes Baumdiagramm
Gegeben sind die Wahrscheinlichkeiten \(P(W) = 0{,}6\), \(P_{W}(K) = 0{,}3\) (vgl. Abiturskript - 3.1.5 Bedingte Wahrscheinlichkeit) und \(P(\overline{W} \cap \overline{K}) = 0{,}1\).
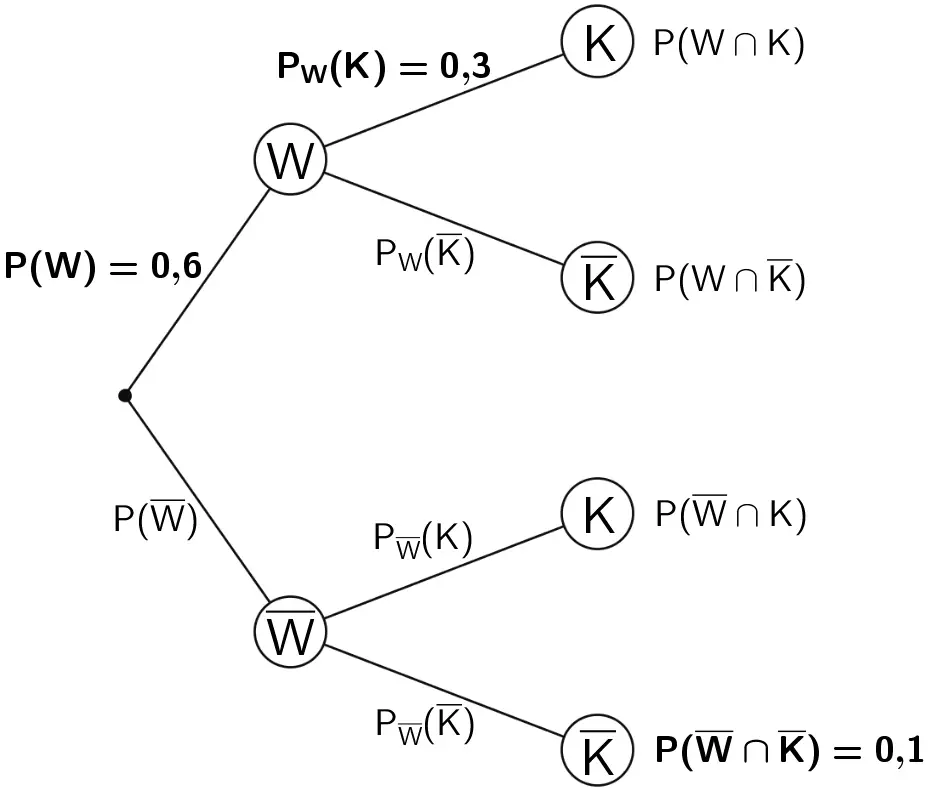
Baumdiagramm mit den Eintragungen der gegebenen Wahrscheinlichkeiten \(P(W)\), \(P_{W}(K)\) und \(P(\overline{W} \cap \overline{K})\)
Verzweigungsregel (Knotenregel) anwenden:
\[\begin{align*}P(W) + P(\overline{W}) &= 1 \\[0.8em] P(\overline{W}) &= 1 - P(W) \\[0.8em] &= 1 - 0{,}6 \\[0.8em] &= 0{,}4 \end{align*}\]
\[\begin{align*} P_{W}(K) + P_{W}(\overline{K}) &= 1 \\[0.8em] P_{W}(\overline{K}) &= 1 - P_{W}(K) \\[0.8em] &= 1 - 0{,}3 \\[0.8em] &= 0{,}7 \end{align*}\]
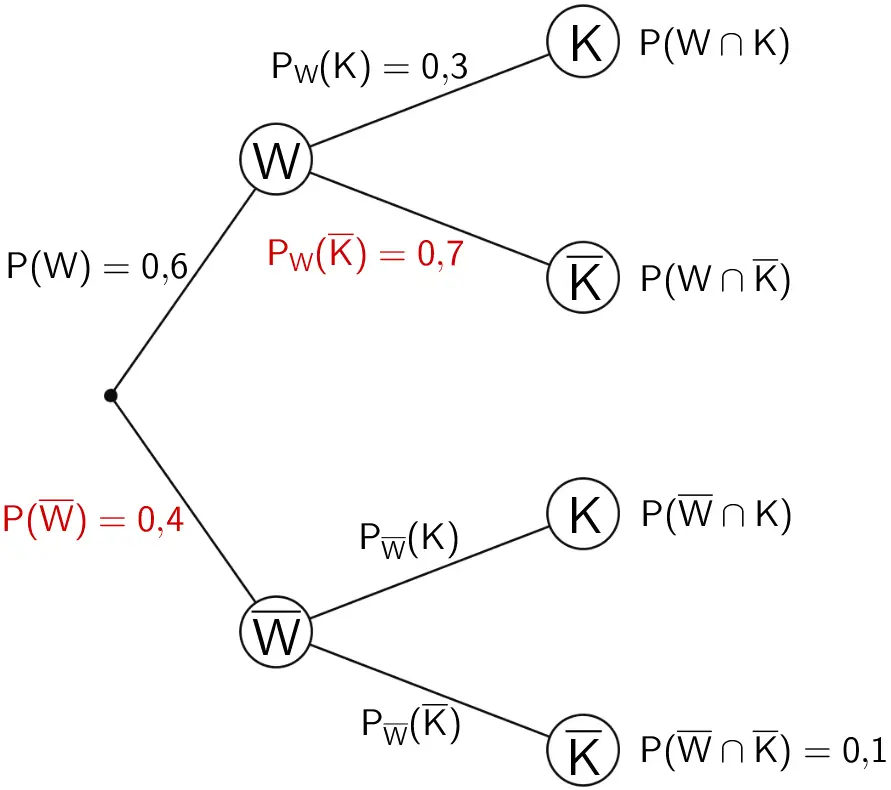
Baumdiagramm mit den Eintragungen der mithilfe der Verzweigungsregel berechneten Wahrscheinlichkeiten \(P(\overline{W})\) und \(P_{W}(\overline{K})\)
1. Pfadregel (Produktregel) anwenden:
\[\begin{align*} P(\overline{W}) \cdot P_{\overline{W}}(\overline{K}) &= P(\overline{W} \cap \overline{K}) \\[0.8em] P_{\overline{W}}(\overline{K}) &= \frac{P(\overline{W} \cap \overline{K})}{P(\overline{W})} \\[0.8em] &= \frac{0{,}1}{0{,}4} \\[0.8em] &= 0{,}25 \end{align*}\]
Verzweigungsregel (Knotenregel) anwenden:
\[\begin{align*} P_{\overline{W}}(K) + P_{\overline{W}}(\overline{K}) &= 1 \\[0.8em] P_{\overline{W}}(K) &= 1 - P_{\overline{W}}(\overline{K}) \\[0.8em] &= 1 - 0{,}25 \\[0.8em] &= 0{,}75 \end{align*}\]
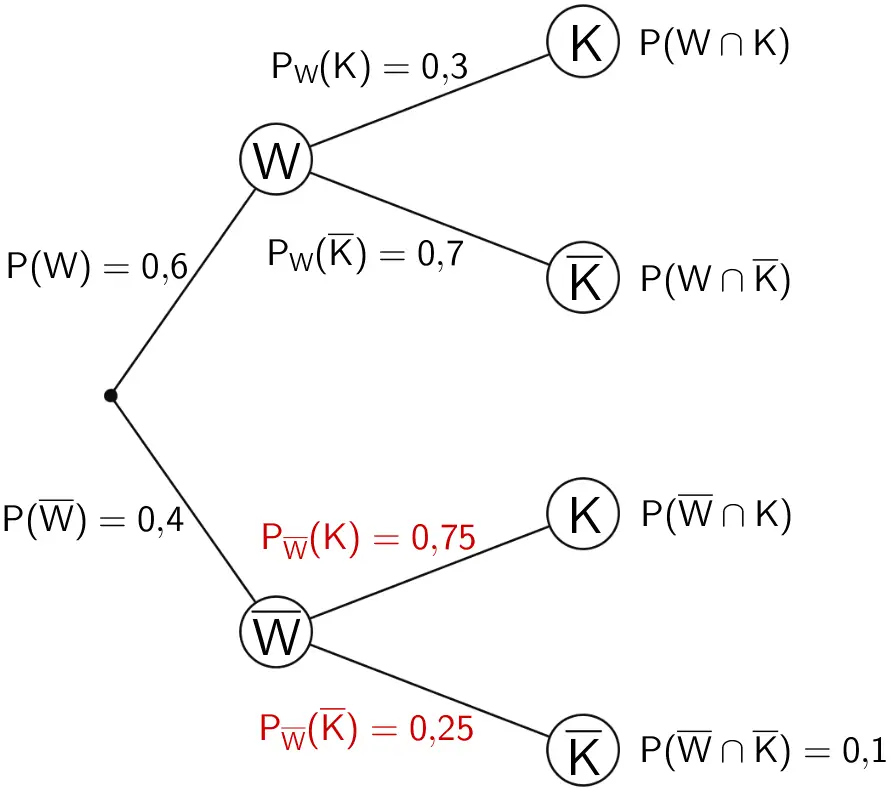
Baumdiagramm mit den Eintragungen der mithilfe der 1. Pfadregel und der Verzweigungsregel berechneten bedingten Wahrscheinlichkeiten \(P_{\overline{W}}(\overline{K})\) und \(P_{\overline{W}}(K)\) (vgl. Abiturskript - 3.1.5 Bedingte Wahrscheinlichkeit)
1. Pfadregel anwenden:
\[P(W \cap K) = P(W) \cdot P_{W}(K) = 0{,}6 \cdot 0{,}3 = 0{,}18\]
\[P(W \cap \overline{K}) = P(W) \cdot P_{W}(\overline{K}) = 0{,}6 \cdot 0{,}7 = 0{,}42\]
\[P(\overline{W} \cap K) = P(\overline{W}) \cdot P_{\overline{W}}(K) = 0{,}4 \cdot 0{,}75 = 0{,}3\]
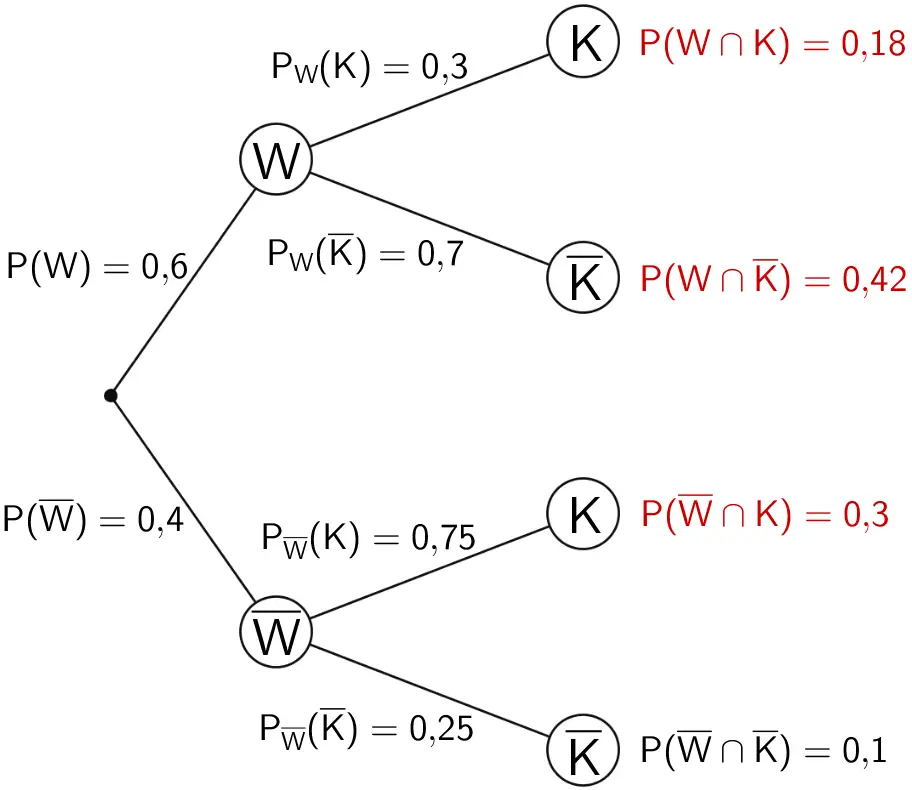
Baumdiagramm mit den Eintragungen der mithilfe der 1. Pfadregel berechneten Wahrscheinlichkeiten der Schnittmengen \(P(W \cap K)\), \(P(W \cap \overline{K})\) und \(P(\overline{W} \cap K)\)
Probe:
Die Summe der Wahrscheinlichkeiten aller Teilmengen (Schnittmengen) ist gleich Eins.
\[\begin{align*}P(\Omega) &= P(W \cap K) + P(W \cap \overline{K}) + P(\overline{W} \cap K) + P(\overline{W} \cap \overline{K}) \\[0.8em] &= 0{,}18 + 0{,}42 + 0{,}3 + 0{,}1 \\[0.8em] &= 1 \end{align*}\]
Wahrscheinlichkeit des Ereignisses „Ein beliebiger Mitarbeiter wählt eine kürzere Strecke."
Das Ereignis \(K\): „Ein beliebiger Mitarbeiter wählt eine kürzere Strecke." enthält die Ergebnisse
\(W \cap K\): „Ein Mitarbeiter entscheidet sich für die Wanderung und die kürzere Strecke." und
\(\overline{W} \cap K\): „Ein Mitarbeiter entscheidet sich für die Fahrradtour und die kürzere Strecke."
2. Pfadregel anwenden:
\[\begin{align*}P(K) &= P(W \cap K) + P(\overline{W} \cap K) \\[0.8em] &= 0{,}18 + 0{,}3 \\[0.8em] &= 0{,}48 \\[0.8em] &= 48\,\% \end{align*}\]
Vierfeldertafel
Mithilfe einer Vierfeldertafel lassen sich die Verknüpfungen zweier Ereignisse \(A\) und \(B\) übersichtlich darstellen und deren absolute Häufigkeiten (Anzahlen) oder Wahrscheinlichkeiten komfortabel ermitteln.
Aufbau einer Vierfeldertafel
Der Ergebnisraum \(\Omega\) zweier Ereignisse \(A\) und \(B\) lässt sich in die vier Teilmengen \(A \cap B\), \(\overline{A} \cap B\), \(A \cap \overline{B}\) und \(\overline{A} \cap \overline{B}\) zerlegen. Jedes Ergebnis \(\omega\) gehört genau einer Teilmenge an. Die absoluten Häufigkeiten oder die Wahrscheinlichkeiten der Ereignisse \(A \cap B\), \(\overline{A} \cap B\), \(A \cap \overline{B}\) und \(\overline{A} \cap \overline{B}\) beschreiben die inneren Zellen einer Vierfeldertafel. Die absoluten Häufigkeiten oder die Wahrscheinlichkeiten der Ereignisse \(A\), \(B\), \(\overline{A}\) und \(\overline{B}\) beschreiben die Randzellen.
| \(A\) | \(\overline{A}\) | ||
| \(B\) | \(\vert A \cap B \vert\) | \(\vert \overline{A} \cap B \vert\) | \(\vert B \vert\) |
| \(\overline{B}\) | \(\vert A \cap \overline{B} \vert\) | \(\vert \overline{A} \cap \overline{B} \vert\) | \(\vert \overline{B} \vert\) |
| \(\vert A \vert\) | \(\vert \overline{A} \vert\) | \(\vert \Omega \vert\) |
Vierfeldertafel der absoluten Häufigkeiten (Anzahlen)
| \(A\) | \(\overline{A}\) | ||
| \(B\) | \(P(A \cap B)\) | \(P(\overline{A} \cap B)\) | \(P(B)\) |
| \(\overline{B}\) | \(P(A \cap \overline{B})\) | \(P(\overline{A} \cap \overline{B})\) | \(P(\overline{B})\) |
| \(P(A)\) | \(P(\overline{A})\) | \(P(\Omega)\) |
Vierfeldertafel der Wahrscheinlichkeiten
Welche Variante der Vierfeldertafel zum Einsatz kommt, hängt von der gegebenen Information ab. Liegen die Anzahlen der Ereignisse vor und sollen die Wahrscheinlichkeiten ermittelt werden, kann zunächst eine Vierfeldertafel der absoluten Häufigkeiten übersichtlicher sein, um anschließend daraus über die relativen Häufigkeiten die Wahrscheinlichkeiten zu bestimmen.
Mit der Vierfeldertafel arbeiten
Bei einer Vierfeldertafel errechnen sich die Einträge der Randzellen zeilen- bzw. spaltenweise aus der Summe der Einträge der inneren Zellen.
| \(A\) | \(\overline{A}\) | ||
| \(B\) | \(10\) | \(30\) | \(40\) |
| \(\overline{B}\) | \(50\) | \(10\) | \(60\) |
| \(60\) | \(40\) | \(100\) |
Vierfeldertafel der absoluten Häufigkeiten (Anzahlen)
| \(A\) | \(\overline{A}\) | ||
| \(B\) | \(0{,}1\) | \(0{,}3\) | \(0{,}4\) |
| \(\overline{B}\) | \(0{,}5\) | \(0{,}1\) | \(0{,}6\) |
| \(0{,}6\) | \(0{,}4\) | \(1\) |
Vierfeldertafel der Wahrscheinlichkeiten
Um eine Vierfeldertafel vollständig ausfüllen zu können, muss eine der folgenden Kombinationen an Informationen vorliegen (Zahlenbeispiele):
Je ein Eintrag zu den Ereignissen \(A\) und \(B\) bzw. den Gegenereignissen \(\overline{A}\) und \(\overline{B}\) und ein Eintrag zu einer Teilmenge der Ereignisse:
| \(A\) | \(\overline{A}\) | ||
| \(B\) | \(\mathbf{0{,}1}\) | \(\textcolor{#e74c3c}{0{,}3}\) | \(\mathbf{0{,}4}\) |
| \(\overline{B}\) | \(\textcolor{#e74c3c}{0{,}5}\) | \(\textcolor{#e74c3c}{0{,}1}\) | \(\textcolor{#e74c3c}{0{,}6}\) |
| \(\mathbf{0{,}6}\) | \(\textcolor{#e74c3c}{0{,}4}\) | \(1\) |
Drei Einträge zu drei der vier möglichen Teilmengen der Ereignisse \(A\) und \(B\) bzw. der Gegenereignisse \(\overline{A}\) und \(\overline{B}\):
| \(A\) | \(\overline{A}\) | ||
| \(B\) | \(\textcolor{#e74c3c}{0{,}1}\) | \(\mathbf{0{,}3}\) | \(\textcolor{#e74c3c}{0{,}4}\) |
| \(\overline{B}\) | \(\mathbf{0{,}5}\) | \(\mathbf{0{,}1}\) | \(\textcolor{#e74c3c}{0{,}6}\) |
| \(\textcolor{#e74c3c}{0{,}6}\) | \(\textcolor{#e74c3c}{0{,}4}\) | \(1\) |
Zwei Einträge zu den Teilmengen \(A \cap B\) und \(\overline{A} \cap \overline{B}\) oder \(A \cap \overline{B}\) und \(\overline{A} \cap B\) und ein beliebiger Eintrag zu den Ereignissen \(A\) oder \(B\) bzw. den Gegenereignissen \(\overline{A}\) oder \(\overline{B}\):
| \(A\) | \(\overline{A}\) | ||
| \(B\) | \(\mathbf{0{,}1}\) | \(\textcolor{#e74c3c}{0{,}3}\) | \(\textcolor{#e74c3c}{0{,}4}\) |
| \(\overline{B}\) | \(\textcolor{#e74c3c}{0{,}5}\) | \(\mathbf{0{,}1}\) | \(\textcolor{#e74c3c}{0{,}6}\) |
| \(\mathbf{0{,}6}\) | \(\textcolor{#e74c3c}{0{,}4}\) | \(1\) |
| \(A\) | \(\overline{A}\) | ||
| \(B\) | \(\textcolor{#e74c3c}{0{,}1}\) | \(\mathbf{0{,}3}\) | \(\textcolor{#e74c3c}{0{,}4}\) |
| \(\overline{B}\) | \(\mathbf{0{,}5}\) | \(\textcolor{e74c3c}{0{,}1}\) | \(\mathbf{0{,}6}\) |
| \(\textcolor{#e74c3c}{0{,}6}\) | \(\textcolor{#e74c3c}{0{,}4}\) | \(1\) |
Beispiel (Variation des Beispiels zum Baumdiagramm):
Auf Wunsch der Mitarbeiter veranstaltet eine Firma einen sportlichen Betriebsausflug. Alle Mitarbeiter nehmen daran teil. Die Mitarbeiter können zwischen einer Wanderung und einem Fahrradausflug wählen. Außerdem besteht die Möglichkeit, sich jeweils für eine kürzere oder eine längere Strecke zu entscheiden. 60 % der Mitarbeiter entscheiden sich für eine Wanderung. 30 % der Mitarbeiter wählen die kürzere Strecke. 90 % aller Mitarbeiter nehmen an dem Fahrradausflug teil oder wählen die längere Strecke.
Erstellen Sie eine vollständig ausgefüllte Vierfeldertafel und geben Sie die Wahrscheinlichkeit dafür an, dass ein beliebiger Mitarbeiter sich für die Wanderung entscheidet oder eine kürzere Strecke wählt.
Die Ereignisse können beispielsweise wie folgt festgelegt werden:
\(W\): „Ein Mitarbeiter entscheidet sich für die Wanderung."
\(\overline{W}\): „Ein Mitarbeiter entscheidet sich für den Fahrradausflug."
\(K\): „Ein Mitarbeiter entscheidet sich für die kürzere Strecke."
\(\overline{K}\): „Ein Mitarbeiter entscheidet sich für die längere Strecke."
Vollständig ausgefüllte Vierfeldertafel
Gegeben sind die Wahrscheinlichkeiten \(P(W) = 0{,}6\), \(P(K) = 0{,}3\) und \(P(\overline{W} \cup \overline{K}) = 0{,}4\).
Es gilt:
\(\overline{W} \cup \overline{K} = (\overline{W} \cap K) \cup (W \cap \overline{K}) \cup (\overline{W} \cap \overline{K})\)
(vgl. 3.1.1 Ereignisse, Verknüpfungen von Ereignissen).
Demnach besetzt die Wahrscheinlichkeit \(P(\overline{W} \cup \overline{K})\) drei innere Zellen der Vierfeldertafel. Mit dieser Information lässt sich die Vierfeldertafel noch nicht bearbeiten.
| \(W\) | \(\overline{W}\) | ||
| \(K\) | \(\mathbf{0{,}3}\) | ||
| \(\overline{K}\) | \(\mathbf{0{,}9}\) | ||
| \(\mathbf{0{,}6}\) | \(1\) |
Vierfeldertafel mit den Eintragungen der gegebenen Wahrscheinlichkeiten
Um die Vierfeldertafel vollständig ausfüllen zu können, wird die Wahrscheinlichkeit des Ereignisses \(W \cap K\) berechnet.
\[\begin{align*}(W \cap K) \cup \underbrace{(\overline{W} \cap K) \cup (w \cap \overline{W}) \cup (\overline{W} \cap \overline{K})}_{\overline{W} \, \cup \, \overline{K}} &= \Omega \\[0.8em] W \cap K &= \Omega \backslash (\overline{W} \cup \overline{K}) \end{align*}\]
\[\begin{align*}\Longrightarrow \quad P(W \cap K) &= 1 - P(\overline{W} \cup \overline{K}) \\[0.8em] &= 1 - 0{,}9 \\[0.8em] &= 0{,}1 \end{align*}\]
Oder unter Anwendung des Gesetzes von De Morgan \(\overline{A} \cup \overline{B} = \overline{A \cap B}\):
\[\begin{align*}\overline{W} \cup \overline{K} &= \overline{W \cap K} \\[0.8em] \overline{W} \cup \overline{K} &= \Omega \backslash (W \cap K) \\[0.8em] \Omega \backslash (\overline{W} \cup \overline{K}) &= W \cap K \end{align*}\]
\[\begin{align*}\Longrightarrow \quad P(W \cap K) &= 1 - P(\overline{W} \cup \overline{K}) \\[0.8em] &= 1 - 0{,}9 \\[0.8em] &= 0{,}1 \end{align*}\]
| \(W\) | \(\overline{W}\) | ||
| \(K\) | \(\mathbf{\textcolor{#e74c3c}{0{,}1}}\) | \(\mathbf{0{,}3}\) | |
| \(\overline{K}\) | |||
| \(\mathbf{0{,}6}\) | \(1\) |
Die Vierfeldertafel kann nun zeilen- bzw. spaltenweise durch Subtraktion oder Addition vervollständigt werden.
Beispielsweise wie folgt:
\[P(\overline{W}) = 1 - P(W) = 1 - 0{,}6 = 0{,}4\]
\[P(\overline{K}) = 1 - P(K) = 1 - 0{,}3 = 0{,}7\]
| \(W\) | \(\overline{W}\) | ||
| \(K\) | \(\mathbf{\textcolor{#e74c3c}{0{,}1}}\) | \(\mathbf{0{,}3}\) | |
| \(\overline{K}\) | \(\textcolor{#e74c3c}{0{,}7}\) | ||
| \(\mathbf{0{,}6}\) | \(\textcolor{#e74c3c}{0{,}4}\) | \(1\) |
\[\begin{align*}P(K \cap \overline{W}) &= P(K) - P(K \cap W) \\[0.8em] &= 0{,}3 - 0{,}1 \\[0.8em] &= 0{,}2 \end{align*}\]
\[\begin{align*}P(W \cap \overline{K}) &= P(W) - P(W \cap K) \\[0.8em] &= 0{,}6 - 0{,}1 \\[0.8em] &= 0{,}5 \end{align*}\]
| \(W\) | \(\overline{W}\) | ||
| \(K\) | \(\mathbf{\textcolor{#e74c3c}{0{,}1}}\) | \(\textcolor{#e74c3c}{0{,}2}\) | \(\mathbf{0{,}3}\) |
| \(\overline{K}\) | \(\textcolor{#e74c3c}{0{,}5}\) | \(\textcolor{#e74c3c}{0{,}7}\) | |
| \(\mathbf{0{,}6}\) | \(\textcolor{#e74c3c}{0{,}4}\) | \(1\) |
\[\begin{align*}P(\overline{K} \cap \overline{W}) &= P(\overline{K}) - P(W \cap \overline{K}) \\[0.8em] &= 0{,}7 - 0{,}5 \\[0.8em] &= 0{,}2 \end{align*}\]
oder
\[\begin{align*}P(\overline{W} \cap \overline{K}) &= P(\overline{W}) - P(\overline{W} \cap K) \\[0.8em] &= 0{,}4 - 0{,}2 \\[0.8em] &= 0{,}2 \end{align*}\]
| \(W\) | \(\overline{W}\) | ||
| \(K\) | \(\mathbf{\textcolor{#e74c3c}{0{,}1}}\) | \(\textcolor{#e74c3c}{0{,}2}\) | \(\mathbf{0{,}3}\) |
| \(\overline{K}\) | \(\textcolor{#e74c3c}{0{,}5}\) | \(\textcolor{#e74c3c}{0{,}2}\) | \(\textcolor{#e74c3c}{0{,}7}\) |
| \(\mathbf{0{,}6}\) | \(\textcolor{#e74c3c}{0{,}4}\) | \(1\) |
Wahrscheinlichkeit, dass sich ein beliebiger Mitarbeiter für die Wanderung entscheidet oder eine kürzere Strecke wählt
Gesucht ist die Wahrscheinlichkeit für das Ereignis \(W \cup K\).
\(W \cup K\): „Ein Mitarbeiter entscheidet sich für die Wanderung oder eine kürzere Strecke oder die kürzere Wanderung."
\(W \cup K = (W \cap \overline{K}) \cup (\overline{W} \cap K) \cup (W \cap K)\)
Die Wahrscheinlichkeit \(P(W \cup K)\) kann mithilfe der ausgefüllten Vierfeldertafel angegeben werden.
| \(W\) | \(\overline{W}\) | ||
| \(K\) | \(\mathbf{\textcolor{#e74c3c}{0{,}1}}\) | \(\textcolor{#e74c3c}{0{,}2}\) | \(\mathbf{0{,}3}\) |
| \(\overline{K}\) | \(\textcolor{#e74c3c}{0{,}5}\) | \(\textcolor{#e74c3c}{0{,}2}\) | \(\textcolor{#e74c3c}{0{,}7}\) |
| \(\mathbf{0{,}6}\) | \(\textcolor{#e74c3c}{0{,}4}\) | \(1\) |
\[\begin{align*}P(W \cup K) &= P(W \cap \overline{K}) + P(\overline{W} \cap K) + P(W \cap K) \\[0.8em] &= 0{,}5 + 0{,}2 + 0{,}1 \\[0.8em] &= 0{,}8 \\[0.8em] &= 80 \, \% \end{align*}\]
Vergleich: Baumdiagramm - Vierfeldertafel
Mit den Informationen einer Vierfeldertafel zweier Ereignisse \(A\) und \(B\) lässt sich auf zweierlei Weise ein zweistufiges Baumdiagramm darstellen. Je nach Wahl der ersten Stufe erscheinen im Baumdiagramm unterschiedliche Informationen der Vierfeldertafel.
Die bedingten Wahrscheinlichkeiten ergeben sich bei einer Vierfeldertafel als Quotient aus einem Eintrag einer inneren Zelle und einem Eintrag einer Randzelle (vgl. Abiturskript - 3.1.5 Bedingte Wahrscheinlichkeit).
Beispiele:
\[P_{A}(B) = \dfrac{P(A \cap B)}{P(A)}\]
\[P_{B}(A) = \frac{P(A \cap B)}{P(B)}\]
| \(A\) | \(\overline{A}\) | ||
| \(B\) | \(P(A \cap B)\) | \(P(\overline{A} \cap B)\) | \(P(B)\) |
| \(\overline{B}\) | \(P(A \cap \overline{B})\) | \(P(\overline{A} \cap \overline{B})\) | \(P(\overline{B})\) |
| \(P(A)\) | \(P(\overline{A})\) | \(1\) |
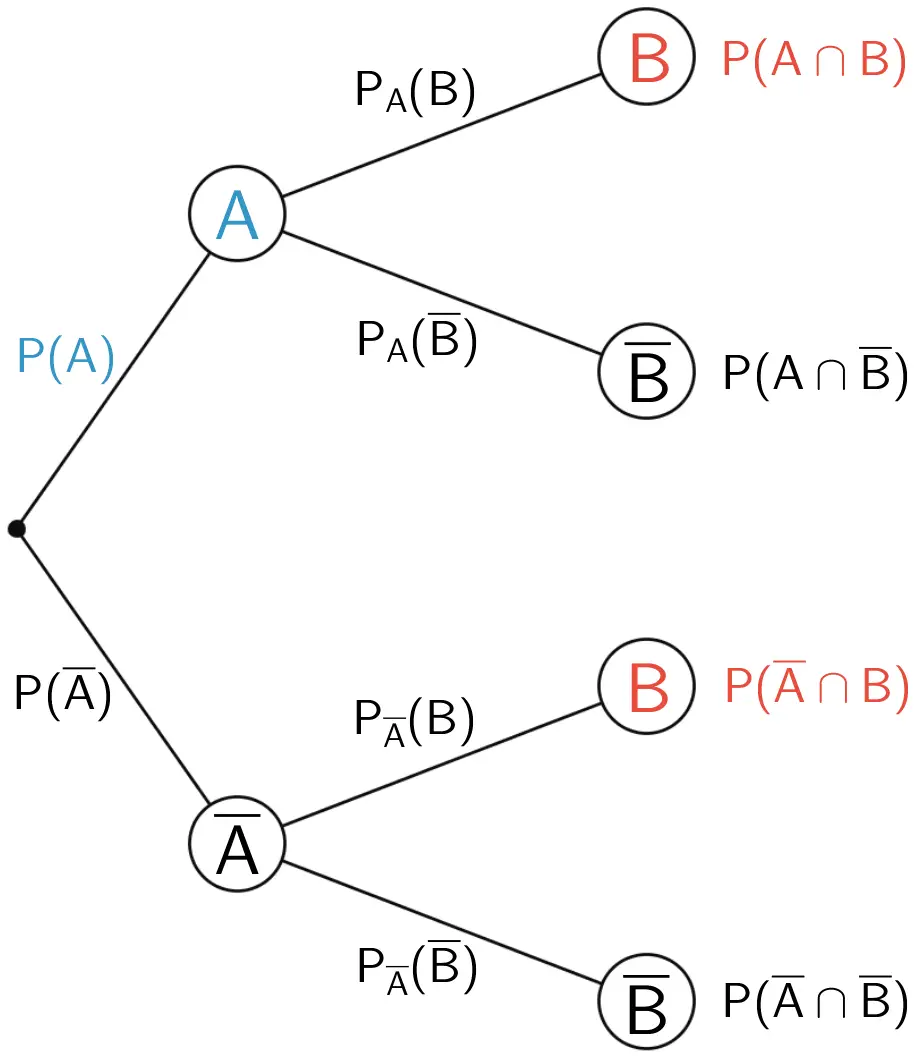
\(\textcolor{#e74c3c}{P(B) = P(A \cap B) + P(\overline{A} \cap B)}\) (2. Pfadregel)
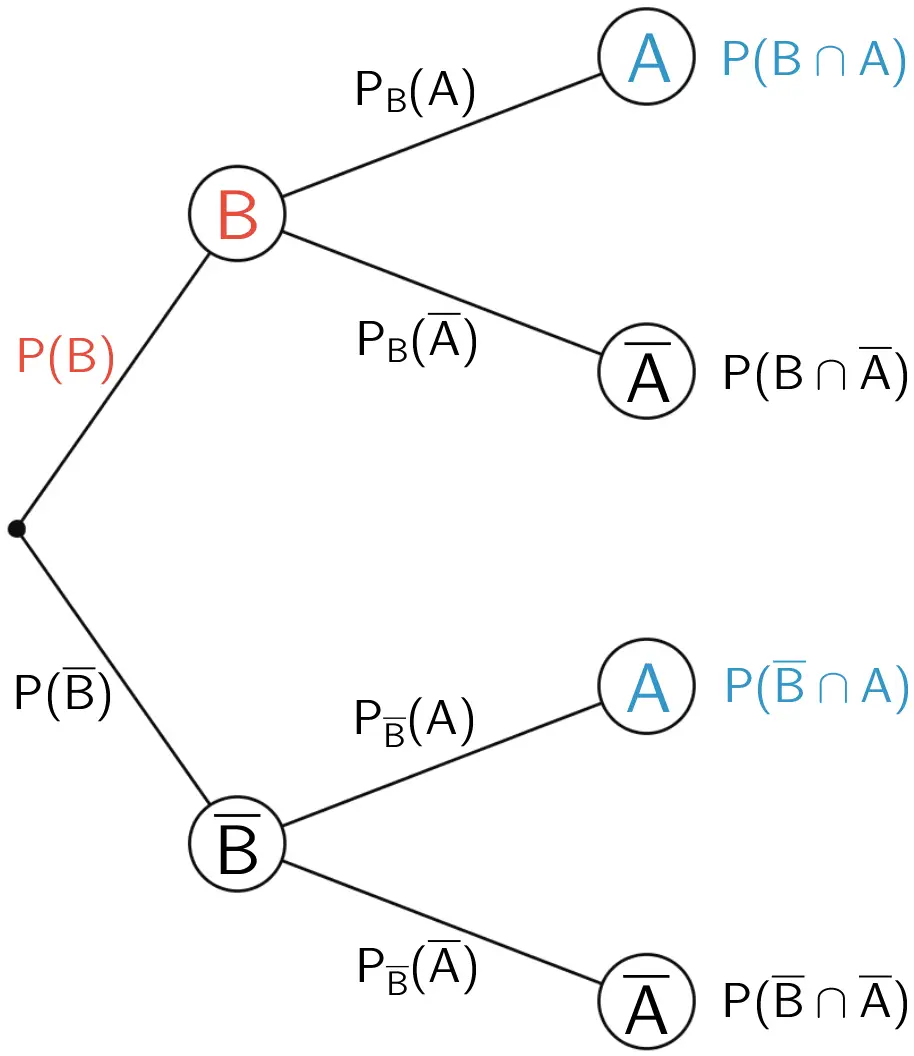
\(\textcolor{#3395c5}{P(A) = P(B \cap A) + P(\overline{B} \cap A)}\) (2. Pfadregel)
Ob man sich bei der Darstellung eines Zufallsexperiments besser für eine Vierfeldertafel oder ein Baumdiagramm entscheidet, hängt von den gegebenen Daten ab. Grundsätzlich ist immer beides möglich. Häufig legen die Daten eines Zufallsexperiments das Ereignis für die erste Stufe eines Baumdiagramms fest.
Beispielaufgabe
Auf dem Fahrradabstellplatz eines Bahnhofs stehen 480 Fahrräder. 70 % der Fahrräder sind Mountainbikes. Bei 96 Mountainbikes erfüllt die Beleuchtung nicht die Straßenverkehrs-Zulassungs-Ordnung (StVZO). Von allen abgestellten Fahrrädern haben 288 eine Beleuchtung nach StVZO.
Erstellen Sie zu der beschriebenen Situation eine vollständig ausgefüllte Viefeldertafel oder ein vollständig beschriftetes Baumdiagramm und berechnen Sie die Wahrscheinlichkeit dafür, dass ein zufällig ausgewähltes Fahrrad kein Mountainbike ist oder eine Beleuchtung nach StVZO hat.
Ereignisse festlegen:
\(M\): „Fahrrad ist ein Mountainbike."
\(\overline{M}\): „Fahrrad ist kein Mountainbike."
\(S\): „Fahrradbeleuchtung erfüllt die StVZO."
\(\overline{S}\): „Fahrradbeleuchtung erfüllt nicht die StVZO."
Die Angabe nennt hauptsächlich die absoluten Häufigkeiten (Anzahlen) der Ereignisse und keine bedingte Wahrscheinlichkeiten. Es bietet sich deshalb an, eine Vierfeldertafel zu erstellen. Zur besseren Übersicht kann zunächst eine Vierfeldertafel der absoluten Häufigkeiten gewählt werden.
Da die Wahrscheinlichkeit dafür, ein beliebiges Fahrrad auszuwählen (Elementarereignis) stets \(\frac{1}{480}\) beträgt, liegt ein Laplace-Experiment vor. Die Wahrscheinlichkeiten der Ereignisse können folglich mithilfe Formel für die Laplace-Warscheinlichkeit berechnet werden (vgl. Abiturskript - 3.1.3 Laplace-Experiment, Laplace-Wahrscheinlichkeit).
Vollständig ausgefüllte Vierfeldertafel
Vierfeldertafel mit den Eintragungen der gegebene Anzahlen bzw. der daraus berechneten Wahrscheinlichkeiten:
\[\vert \Omega \vert = 480\]
\[\vert M \vert = 0{,}7 \cdot \vert \Omega \vert = 0{,}7 \cdot 480 = 336\]
\[\vert M \cap \overline{S} \vert = 96\]
\[\vert S \vert = 288\]
| \(M\) | \(\overline{M}\) | ||
| \(S\) | \(\mathbf{288}\) | ||
| \(\overline{S}\) | \(\mathbf{96}\) | ||
| \(\mathbf{336}\) | \(\mathbf{480}\) |
Vierfeldertafel der absoluten Häufigkeiten (Anzahlen)
\[P(M) = \frac{\vert M \vert}{\vert \Omega \vert} = \frac{336}{480} = 0{,}7\]
\[P(M \cap \overline{S}) = \frac{\vert M \cap \overline{S} \vert}{\vert \Omega \vert} = \frac{96}{480} = 0{,}2\]
\[P(S) = \frac{\vert S \vert}{\vert \Omega \vert} = \frac{288}{480} = 0{,}6\]
| \(M\) | \(\overline{M}\) | ||
| \(S\) | \(\mathbf{0{,}6}\) | ||
| \(\overline{S}\) | \(\mathbf{0{,}2}\) | ||
| \(\mathbf{0{,}7}\) | \(\mathbf{1}\) |
Vierfeldertafel der Wahrscheinlichkeiten
Vierfeldertafel zeilen- bzw. spaltenweise durch Subtraktion oder Addition vervollständigen:
\[\vert \overline{M} \vert = \vert \Omega \vert - \vert M \vert = 480 - 336 = 144\]
\[\begin{align*}\vert M \cap S \vert &= \vert M \vert - \vert M \cap \overline{S} \vert \\[0.8em] &= 336 - 96 \\[0.8em] &= 240 \end{align*}\]
\[\vert \overline{S} \vert = \vert \Omega \vert - \vert S \vert = 480 - 288 = 192\]
| \(M\) | \(\overline{M}\) | ||
| \(S\) | \(\textcolor{#e74c3c}{240}\) | \(\mathbf{288}\) | |
| \(\overline{S}\) | \(\mathbf{96}\) | \(\textcolor{#e74c3c}{192}\) | |
| \(\mathbf{336}\) | \(\textcolor{#e74c3c}{144}\) | \(\mathbf{480}\) |
Vierfeldertafel der absoluten Häufigkeiten (Anzahlen)
\[P(\overline{M}) = 1 - P(M) = 1 - 0{,}7 = 0{,}3\]
\[\begin{align*}P(M \cap S) &= P(M) - P(M \cap \overline{S}) \\[0.8em] &= 0{,}7 - 0{,}2 \\[0.8em] &= 0{,}5 \end{align*}\]
\[P(\overline{S}) = 1 - P(S) = 1 - 0{,}6 = 0{,}4\]
| \(M\) | \(\overline{M}\) | ||
| \(S\) | \(\textcolor{#e74c3c}{0{,}5}\) | \(\mathbf{0{,}6}\) | |
| \(\overline{S}\) | \(\mathbf{0{,}2}\) | \(\textcolor{#e74c3c}{0{,}4}\) | |
| \(\mathbf{0{,}7}\) | \(\textcolor{#e74c3c}{0{,}3}\) | \(\mathbf{1}\) |
Vierfeldertafel der Wahrscheinlichkeiten
\[\begin{align*}\vert \overline{M} \cap S \vert &= \vert S \vert - \vert M \cap S \vert \\[0.8em] &= 288 - 240 \\[0.8em] &= 48 \end{align*}\]
\[\begin{align*}\vert \overline{M} \cap \overline{S} \vert &= \vert \overline{S} \vert - \vert M \cap \overline{S} \vert \\[0.8em] &= 192 - 96 \\[0.8em] &= 96 \end{align*}\]
| \(M\) | \(\overline{M}\) | ||
| \(S\) | \(\textcolor{#e74c3c}{240}\) | \(\textcolor{#e74c3c}{48}\) | \(\mathbf{288}\) |
| \(\overline{S}\) | \(\mathbf{96}\) | \(\textcolor{#e74c3c}{96}\) | \(\textcolor{#e74c3c}{192}\) |
| \(\mathbf{336}\) | \(\textcolor{#e74c3c}{144}\) | \(\mathbf{480}\) |
Vierfeldertafel der absoluten Häufigkeiten (Anzahlen)
\[\begin{align*}P(\overline{M} \cap S) &= P(S) - P(M \cap S) \\[0.8em] &= 0{,}6 - 0{,}5 \\[0.8em] &= 0{,}1 \end{align*}\]
\[\begin{align*}P(\overline{M} \cap \overline{S}) &= P(\overline{S}) - P(M \cap \overline{S}) \\[0.8em] &= 0{,}4 - 0{,}2 \\[0.8em] &= 0{,}2 \end{align*}\]
| \(M\) | \(\overline{M}\) | ||
| \(S\) | \(\textcolor{#e74c3c}{0{,}5}\) | \(\textcolor{#e74c3c}{0{,}1}\) | \(\mathbf{0{,}6}\) |
| \(\overline{S}\) | \(\mathbf{0{,}2}\) | \(\textcolor{#e74c3c}{0{,}2}\) | \(\textcolor{#e74c3c}{0{,}4}\) |
| \(\mathbf{0{,}7}\) | \(\textcolor{#e74c3c}{0{,}3}\) | \(\mathbf{1}\) |
Vierfeldertafel der Wahrscheinlichkeiten
Wahrscheinlichkeit, dass ein zufällig ausgewähltes Fahrrad kein Mountainbike ist oder eine Beleuchtung nach StVZO hat
Gesucht ist die Wahrscheinlichkeit für das Ereignis \(\overline{M} \cup S\).
\(\overline{M} \cup S\): „Ein zufällig ausgewähltes Fahrrad ist kein Mountainbike oder hat eine Beleuchtung nach StVZO oder ist kein Mountainbike und hat eine Beleuchtung nach StVZO."
\(\overline{M} \cup S = (\overline{M} \cap \overline{S}) \cup (M \cap S) \cup (\overline{M} \cap S)\)
Die Wahrscheinlichkeit \(P(\overline{M} \cup S)\) kann mithilfe der ausgefüllten Vierfeldertafel berechnet werden.
| \(M\) | \(\overline{M}\) | ||
| \(S\) | \(\textcolor{#e74c3c}{0{,}5}\) | \(\textcolor{#e74c3c}{0{,}1}\) | \(\mathbf{0{,}6}\) |
| \(\overline{S}\) | \(\mathbf{0{,}2}\) | \(\textcolor{#e74c3c}{0{,}2}\) | \(\textcolor{#e74c3c}{0{,}4}\) |
| \(\mathbf{0{,}7}\) | \(\textcolor{#e74c3c}{0{,}3}\) | \(\mathbf{1}\) |
\[\begin{align*}P(\overline{M} \cup S) &= P(\overline{M} \cap \overline{S}) + P(M \cap S) + P(\overline{M} \cap S) \\[0.8em] &= 0{,}2 + 0{,}5 + 0{,}1 \\[0.8em] &= 0{,}8 \\[0.8em] &= 80 \, \% \end{align*}\]
Vollständig beschriftetes Baumdiagramm
Die Aufgabe verlangt wahlweise nach einer Vierfeldertafel oder einem Baumdiagramm. Zum Vergleich mit der bereits vollständig ausgefüllten Vierfeldertafel wird das vollständig beschriftete Baumdiagramm erstellt.
Ereignisse:
\(M\): „Fahrrad ist ein Mountainbike."
\(\overline{M}\): „Fahrrad ist kein Mountainbike."
\(S\): „Fahrradbeleuchtung erfüllt die StVZO."
\(\overline{S}\): „Fahrradbeleuchtung erfüllt nicht die StVZO."
Gegeben:
\[\vert \Omega \vert = 480\]
\[P(M) = 0{,}7\]
\[\vert M \cap \overline{S} \vert = 96 \quad \Longrightarrow \quad P(M \cap \overline{S}) = \frac{\vert M \cap \overline{S} \vert}{\vert \Omega \vert} = \frac{96}{480} = 0{,}2\]
\[\vert S \vert = 288 \quad \Longrightarrow \quad P(S) = \frac{\vert S \vert}{\vert \Omega \vert} = \frac{288}{480} = 0{,}6\]
Da die Wahrscheinlichkeiten des Ereignisses \(M\) und des Ereignisses \(S\) gegeben sind, kann für die erste Stufe des Baumdiagramms eines der beiden Ereignisse gewählt werden. Nachfolgend wird der Lösungsweg für das Baumdiagramm beginnend mit dem Ereignis \(M\) beschrieben. Der Lösungsweg gilt entsprechend für das Baumdiagramm beginnend mit dem Ereignis \(S\).
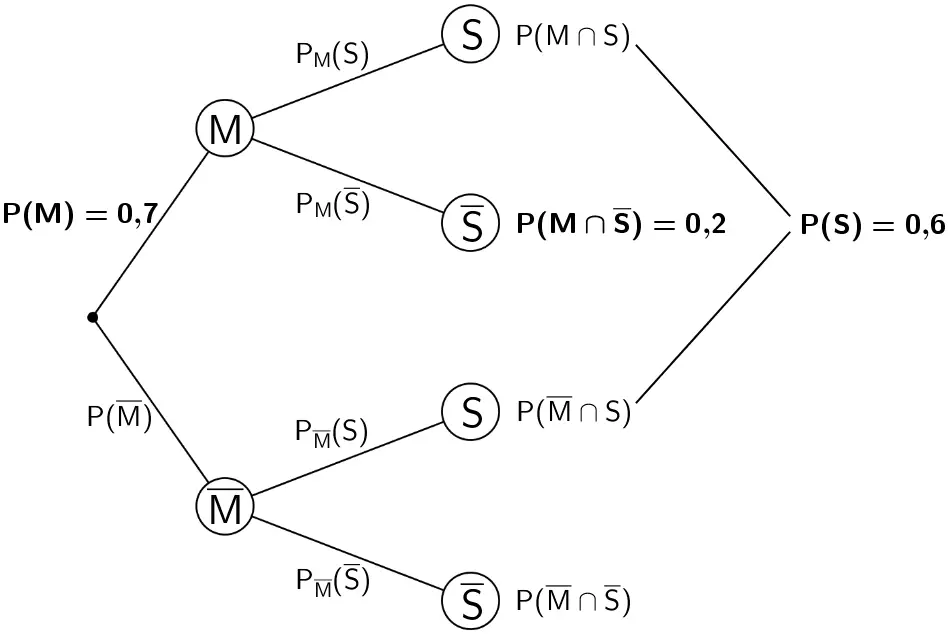
Baumdiagramm mit den Eintragungen der gegebenen Wahrscheinlichkeiten \(P(M)\), \(P(M \cap \overline{S})\) und \(P(S)\)
Verzweigungsregel (Knotenregel) anwenden:
\[\begin{align*}P(M) + P(\overline{M}) &= 1 \\[0.8em] P(\overline{M}) &= 1 - P(M) \\[0.8em] &= 1 - 0{,}7 \\[0.8em] &= 0{,}3\end{align*}\]
\[\begin{align*}P(S) + P(\overline{S}) &= 1 \\[0.8em] P(\overline{S}) &= 1 - P(S) \\[0.8em] &= 1 - 0{,}6 \\[0.8em] &= 0{,}4\end{align*}\]
2. Pfadregel (Summenregel) anwenden:
\[\begin{align*} P(\overline{M} \cap \overline{S}) + P(M \cap \overline{S}) &= P(\overline{S}) \\[0.8em] P(\overline{M} \cap \overline{S}) &= P(\overline{S}) - P(M \cap \overline{S}) \\[0.8em] &= 0{,}4 - 0{,}2 \\[0.8em] &= 0{,}2 \end{align*}\]
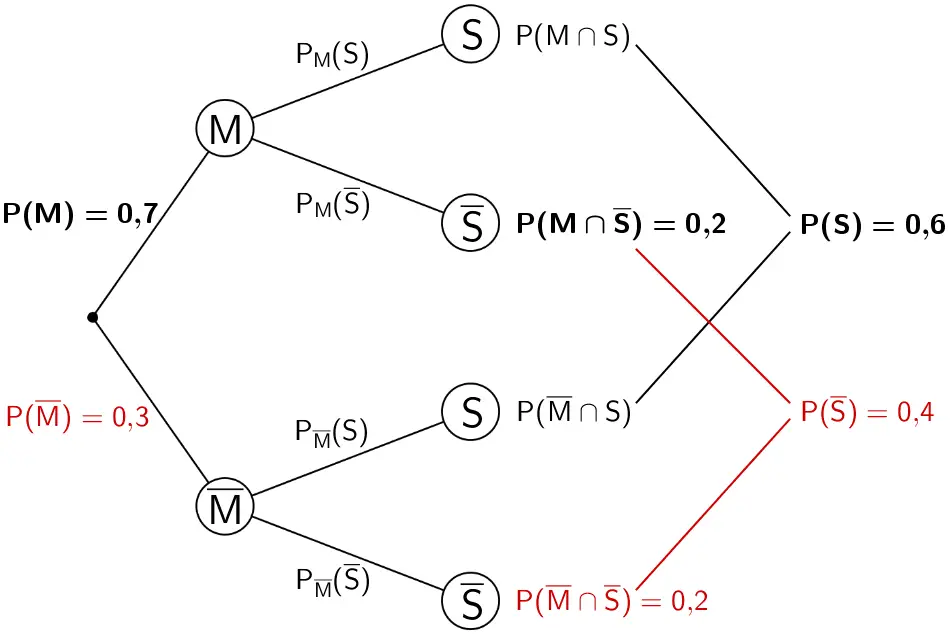
Baumdiagramm mit den Eintragungen der mithilfe der Verzweigungsrege und der 2. Pfadregel berechneten Wahrscheinlichkeiten \(P(\overline{M})\), \(P(\overline{S})\) und \(P(\overline{M} \cap \overline{S})\)
1. Pfadregel (Produktregel) anwenden
\[\begin{align*}P(M) \cdot P_{M}(\overline{S}) &= P(M \cap \overline{S}) \\[0.8em] P_{M}(\overline{S}) &= \frac{P(M \cap \overline{S})}{P(M)} \\[0.8em] &= \frac{0{,}2}{0{,}7} \\[0.8em] &= \frac{2}{7}\end{align*}\]
\[\begin{align*}P(\overline{M}) \cdot P_{\overline{M}}(\overline{S}) &= P(\overline{M} \cap \overline{S}) \\[0.8em] P_{\overline{M}}(\overline{S}) &= \frac{P(\overline{M} \cap \overline{S})}{P(\overline{M})} \\[0.8em] &= \frac{0{,}2}{0{,}3} \\[0.8em] &= \frac{2}{3}\end{align*}\]
Verzweigungsregel (Knotenregel) anwenden:
\[\begin{align*} P_{M}(S) + P_{M}(\overline{S}) &= 1 \\[0.8em] P_{M}(S) &= 1 - P_{M}(\overline{S}) \\[0.8em] &= 1 - \frac{2}{7} \\[0.8em] &= \frac{5}{7} \end{align*}\]
\[\begin{align*} P_{\overline{M}}(S) + P_{\overline{M}}(\overline{S}) &= 1 \\[0.8em] P_{\overline{M}}(S) &= 1 - P_{\overline{M}}(\overline{S}) \\[0.8em] &= 1 - \frac{2}{3} \\[0.8em] &= \frac{1}{3} \end{align*}\]
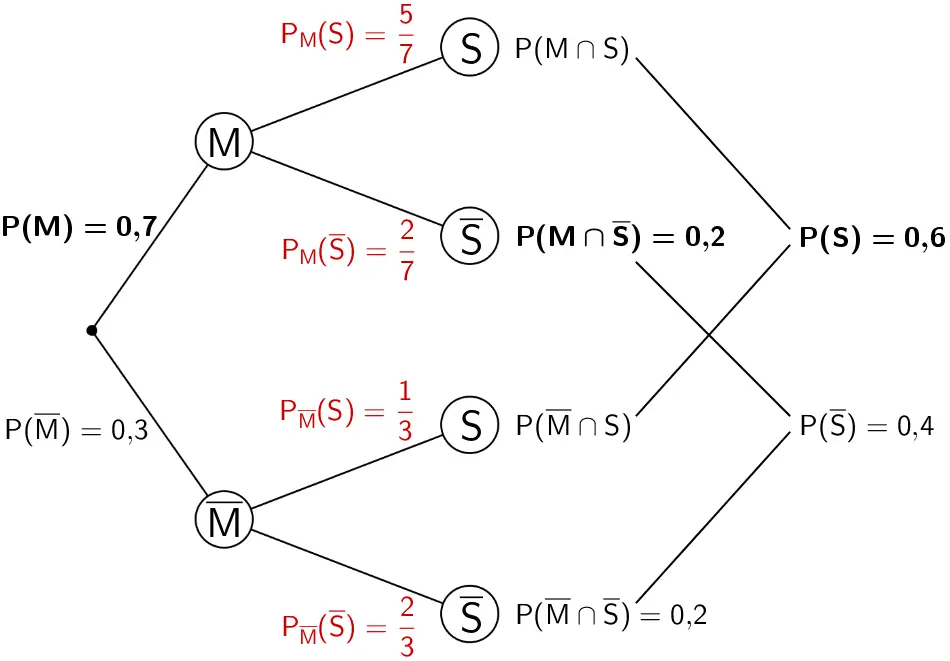
Baumdiagramm mit den Eintragungen der mithilfe der 1. Pfadregel und der Verzweigungsregel berechneten bedingten Wahrscheinlichkeiten \(P_{M}(S)\), \(P_{M}(\overline{S})\), \(P_{\overline{M}}(S)\) und \(P_{\overline{M}}(\overline{S})\) (vgl. Abiturskript - 3.1.5 Bedingte Wahrscheinlichkeit)
1. Pfadregel (Produktregel) anwenden:
\[P(M \cap S) = P(M) \cdot P_{M}(S) = 0{,}7 \cdot \frac{5}{7} = 0{,}5\]
\[P(\overline{M} \cap S) = P(\overline{M}) \cdot P_{\overline{M}}(S) = 0{,}3 \cdot \frac{1}{3} = 0{,}1\]
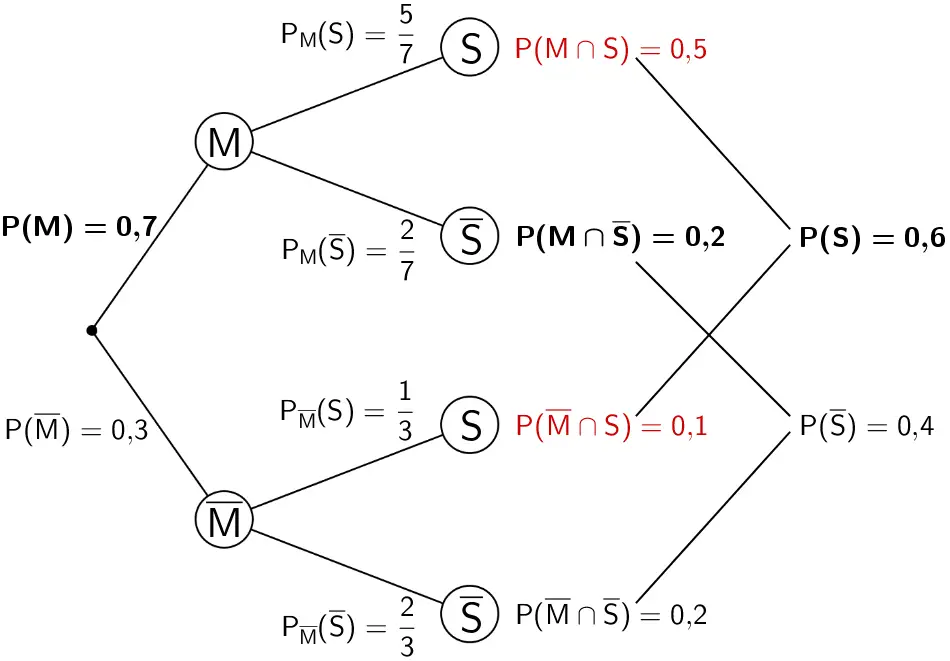
Baumdiagramm mit den Eintragungen der mithilfe der 1. Pfadregel berechneten Wahrscheinlichkeiten \(P(M \cap S)\) und P(\overline{M} \cap S)
Probe:
Die Summe der Wahrscheinlichkeiten aller Teilmengen (Schnittmengen) ist gleich eins.
\[\begin{align*}P(\Omega) &= P(M \cap S) + P(M \cap \overline{S}) + P(\overline{M} \cap S) + P(\overline{M} \cap \overline{S}) \\[0.8em] &= 0{,}5 + 0{,}2 + 0{,}1 + 0{,}2 \\[0.8em] &= 1 \end{align*}\]
Wahrscheinlichkeit, dass ein zufällig ausgewähltes Fahrrad kein Mountainbike ist oder eine Beleuchtung nach StVZO hat
Gesucht ist die Wahrscheinlichkeit für das Ereignis \(\overline{M} \cup S\).
\(\overline{M} \cup S\): „Ein zufällig ausgewähltes Fahrrad ist kein Mountainbike oder hat eine Beleuchtung nach StVZO oder ist kein Mountainbike und hat eine Beleuchtung nach StVZO."
\(\overline{M} \cup S = (\overline{M} \cap \overline{S}) \cup (M \cap S) \cup (\overline{M} \cap S)\)
Die Wahrscheinlichkeit \(P(\overline{M} \cup S)\) kann mithilfe des Baumdiagramms berechnet werden.
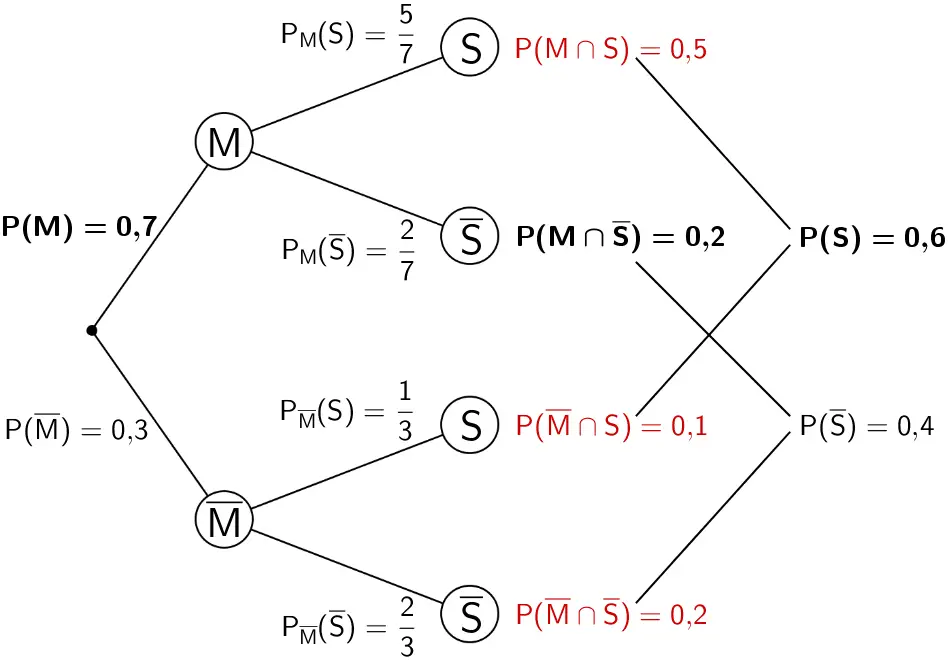
\[\begin{align*}P(\overline{M} \cup S) &= P(\overline{M} \cap \overline{S}) + P(M \cap S) + P(\overline{M} \cap S) \\[0.8em] &= 0{,}2 + 0{,}5 + 0{,}1 \\[0.8em] &= 0{,}8 \\[0.8em] &= 80 \, \% \end{align*}\]

