Orthogonale Wendetangenten
Betrachtet wird die Kurvenschar \(G_{f_{k}}\) einer Funktionenschar \(f_{k}\), welche für bestimmte Werte des Parameters \(k\) zwei Wendepunkte \(W_{1}\) und \(W_{2}\) mit den Wendetangenten \(w_{1}\) und \(w_{2}\) besitzt. Für welchen Wert des Parameters \(k\) sind die beiden Wendetangenten orthogonal (zueinander senkrecht)?
Für die Steigungen \(m_{1}\) und \(m_{2}\) zweier zueinander senkrechter Geraden gilt: \(m_{1} \cdot m_{2} = -1 \enspace \Leftrightarrow \enspace m_{1} = -\dfrac{1}{m_{2}}\) (vgl. Abiturskript - 1.1.1 Lineare Funktion, Steigung einer Geraden)
Die erste Ableitung \(f'_{k}\) der Funktionenschar \(f_{k}\) beschreibt die Steigungen \(m_{w_{1}}\) und \(m_{w_{2}}\) der Wendetangenten \(w_{1}\) und \(w_{2}\) an den Wendestellen \(x_{1}\) bzw. \(x_{2}\) (vgl. Abiturskript - 1.5.1 Die Ableitung, Tangentensteigung).
Somit ergibt sich folgender Ansatz:
\[\begin{align*} m_{w_{1}} &= -\frac{1}{m_{w_{2}}} \\[0.8em] f'_{k}(x_{1}) &= -\frac{1}{f'_{k}(x_{2})} \end{align*}\]
Vorgehensweise
In einem ersten Schritt werden die Wendestellen der Funktionenschar \(f_{k}\) in Abhängigkeit des Parameters \(k\) bestimmt (vgl. 1.7.5 - Seite 1 Extrem- und Wendepunkte einer Kurvenschar bzw. Abiturskript - 1.5.4 Krümmungsverhalten und Wendepunkte). Anschließend ist zu überprüfen, für welche Werte des Parameters \(k\) zwei (verschiedene) Wendestellen vorliegen.
Die Lösung der Gleichung \(f'_{k}(x_{1}) = -\dfrac{1}{f'_{k}(x_{2})}\) liefert schließlich den gesuchten Wert des Parameters \(k\), sodass die Wendetangenten zueinander senkrecht sind.
Beispiel:
Gegeben sei die in \(\mathbb R\) definierte Funktionenschar \(f_{k} \colon x \mapsto 0{,}5kx^{4} - 4kx^{2}\) mit \(k > 0\).
Für welchen Wert des Parameters \(k\) hat der zugehörige Graph der Funktionenschar \(f_{k}\) zwei zueinander senkrechte Wendetangenten?
\[f_{k}(x) = 0{,}5kx^{4} - 4kx^{2}; \; D_{f_{k}} = \mathbb R, \; k > 0\]
Ableitungen \(f'_{k}\), \(f''_{k}\) und \(f'''_{k}\) bilden:
Mit der ersten Ableitung \(f'_{k}\) werden die Steigungen der Wendetangenten beschrieben (vgl. Ansatz oben). Mithilfe der zweiten Ableitung \(f''_{k}\) lassen sich die Wendestellen bestimmen. Die dritte Ableitung \(f'''_{k}\) dient optional für den Nachweis der Wendestellen (vgl. Abiturskript - 1.5.4 Krümmungsverhalten und Wendepunkte). Die Funktionsterme \(f_{k}(x)\), \(f'_{k}(x)\) und \(f''_{k}(x)\) können unter Beachtung der Faktor- und der Summenregel sowie mithilfe der Ableitung einer Potenzfunktion abgeleitet werden. Der Parameter \(k\) wird dabei wie eine Konstante behandelt (vgl. Abiturskript - 1.5.2 Ableitungsregeln).
\[f_{k}(x) = 0{,}5kx^{4} - 4kx^{2}; \; D_{f_{k}}\]
\[\begin{align*}f'_{k}(x) &= 0{,}5k \cdot 4 \cdot x^{3} - 4k \cdot 2 \cdot x \\[0.8em] &= 2kx^{3} - 8kx \end{align*}\]
\[\begin{align*}f''_{k}(x) &= 2k \cdot 3 \cdot x^{2} - 8k \\[0.8em] &= 6kx^{2} - 8k \end{align*}\]
\[\begin{align*} f'''_{k}(x) &= 6k \cdot 2 \cdot x - 0 \\[0.8em] &= 12kx \end{align*}\]
Wendestellen der Funktionenschar \(f_{k}\) ermitteln:
Die Nullstellen von \(f''_{k}\) sind mögliche Wendestellen (vgl. Abiturskript - 1.5.4 Krümmungsverhalten und Wendepunkte).
\[\begin{align*} f''_{k}(x) &= 0 \\[0.8em] 6kx^{2} - 8k &= 0 & &| + 8k \\[0.8em] 6kx^{2} &= 8k & &| : 6k \\[0.8em] x^{2} &= \frac{4}{3} & &| \; \sqrt{\quad} \\[0.8em] x_{1,2} &= \pm \frac{2}{\sqrt{3}} \\[0.8em] &= \pm \frac{2\sqrt{3}}{3} \end{align*}\]
Unabhängig vom Wert des Paraments \(k\) sind \(x_{1} = -\frac{2\sqrt{3}}{3}\) und \(x_{2} = \frac{2\sqrt{3}}{3}\) mögliche Wendestellen der Funktionenschar \(f_{k}\).
Nachweis der Wendestellen \(x_{1}\) und \(x_{2}\):
Die Begründung der Wendestellen kann mithilfe des Vorzeichenwechsels von \(f''_{k}\) oder mithilfe der dritten Ableitung \(f'''_{k}\) erfolgen (vgl. Abiturskript - 1.5.4 Krümmungsverhalten und Wendepunkte).
Begründung mithilfe des Vorzeichenwechsels von \(f''_{k}\):
Der Vorzeichenwechsel von \(f''_{k}\) an den Stellen \(x_{1} = -\frac{2\sqrt{3}}{3}\) und \(x_{2} = \frac{2\sqrt{3}}{3}\) lässt sich besser beurteilen, wenn der Funktionsterm \(f''_{k}(x)\) in der Produktform vorliegt. Unter Berücksichtigung der Nullstellen \(x_{1}\) und \(x_{2}\) von \(f''_{k}\) sowie der 3. Binomischen Formel wird der Funktionsterm \(f''_{k}(x)\) faktorisiert.
\[\begin{align*} f''_{k}(x) &= 6kx^{2} - 8k \\[0.8em] &= 6k \bigg( \underbrace{x^{2} - \frac{4}{3}}_{\large{a^{2}\,-\,b^{2}}} \bigg) \\[0.8em] &= 6k \underbrace{\left( x - \frac{2\sqrt{3}}{3} \right) \left( x + \frac{2\sqrt{3}}{3} \right)}_{\large{(a\,-\,b)(a\,+\,b)}} \enspace (k > 0) \end{align*}\]
\[\left. \begin{align*} &f''_{k}\left( \textstyle -\frac{2\sqrt{3}}{3} \right) = 0 \\[0.8em] &f''_{k}(x) > 0 \; \text{für} \; x < \textstyle -\frac{2\sqrt{3}}{3} \\[0.8em] &f''_{k}{x} < 0 \, \text{für} \; x > \textstyle -\frac{2\sqrt{3}}{3} \end{align*} \right\} \enspace \Rightarrow \enspace \text{Wendepunkte}\; W_{1}\left(\textstyle -\frac{2\sqrt{3}}{3} \, \Big| \, f_{k}\left( \textstyle -\frac{2\sqrt{3}}{3} \right) \right)\]
\[\left. \begin{align*} &f''_{k}\left( \textstyle \frac{2\sqrt{3}}{3} \right) = 0 \\[0.8em] &f''_{k}(x) < 0 \; \text{für} \; x < \textstyle \frac{2\sqrt{3}}{3} \\[0.8em] &f''_{k}{x} > 0 \, \text{für} \; x > \textstyle \frac{2\sqrt{3}}{3} \end{align*} \right\} \enspace \Rightarrow \enspace \text{Wendepunkte}\; W_{2}\left(\textstyle \frac{2\sqrt{3}}{3} \, \Big| \, f_{k}\left( \textstyle \frac{2\sqrt{3}}{3} \right) \right)\]
Veranschaulichung mithilfe einer Krümmungstabelle:
| \((k > 0)\) | \(x < -\frac{2\sqrt{3}}{3}\) | \(x = -\frac{2\sqrt{3}}{3}\) | \(x > -\frac{2\sqrt{3}}{3}\) |
| \(6k\) | \(+\) | \(+\) | \(+\) |
| \(\left(x - \frac{2\sqrt{3}}{3} \right)\) | \(-\) | \(-\) | \(-\) |
| \(\left( x + \frac{2\sqrt{3}}{3} \right)\) | \(-\) | \(0\) | \(+\) |
| \(f''_{k}(x)\) | \(+\) | \(0\) | \(-\) |
| \(G_{f_{k}}\) | \(\style{display: inline-block; transform:rotate(0.5turn);}{\Large \curvearrowleft}\) | \(W_{1}\left(-\frac{2\sqrt{3}}{3}\, \Big| \, f_{k}\left( -\frac{2\sqrt{3}}{3} \right) \right)\) | \(\Large \curvearrowright\) |
| \((k > 0)\) | \(x < \frac{2\sqrt{3}}{3}\) | \(x = \frac{2\sqrt{3}}{3}\) | \(x > \frac{2\sqrt{3}}{3}\) |
| \(6k\) | \(+\) | \(+\) | \(+\) |
| \(\left(x - \frac{2\sqrt{3}}{3} \right)\) | \(-\) | \(0\) | \(+\) |
| \(\left( x + \frac{2\sqrt{3}}{3} \right)\) | \(+\) | \(+\) | \(+\) |
| \(f''_{k}(x)\) | \(-\) | \(0\) | \(+\) |
| \(G_{f_{k}}\) | \(\Large \curvearrowright\) | \(W_{2}\left(\frac{2\sqrt{3}}{3}\, \Big| \, f_{k}\left( \frac{2\sqrt{3}}{3} \right) \right)\) | \(\style{display: inline-block; transform:rotate(0.5turn);}{\Large \curvearrowleft}\) |
Begründung mithilfe der dritten Ableitung \(f'''_{k}\):
\(f'''_{k}(x) = 12kx\) (vgl. oben)
\[k > 0\]
\[\left. \begin{align*} &f''_{k}\left( \textstyle -\frac{2\sqrt{3}}{3} \right) = 0 \\[0.8em] &f'''_{k}\left( \textstyle -\frac{2\sqrt{3}}{3} \right) \neq 0 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Wendepunkte}\; W_{1}\left(\textstyle -\frac{2\sqrt{3}}{3} \, \Big| \, f_{k}\left( \textstyle -\frac{2\sqrt{3}}{3} \right) \right)\]
\[\left. \begin{align*} &f''_{k}\left( \textstyle \frac{2\sqrt{3}}{3} \right) = 0 \\[0.8em] &f'''_{k}\left( \textstyle \frac{2\sqrt{3}}{3} \right) \neq 0 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Wendepunkte}\; W_{2}\left(\textstyle \frac{2\sqrt{3}}{3} \, \Big| \, f_{k}\left( \textstyle \frac{2\sqrt{3}}{3} \right) \right)\]
Die Funktionenschar \(f_{k}\) besitzt die Wendestellen \(x_{1} = -\frac{2\sqrt{3}}{3}\) und \(x_{2} = \frac{2\sqrt{3}}{3}\).
Wert des Parameters \(k\) für orthogonale Wendetangenten berechnen:
\[x_{1} = -\frac{2\sqrt{3}}{3}; \enspace x_{2} = \frac{2\sqrt{3}}{3}\]
\(f'_{k}(x) = 2kx^{3} - 8kx\) (vgl. oben)
\[f'_{k}(x_{1}) = -\frac{1}{f'_{k}(x_{2})}\]
\[\begin{align*}f'_{k}(x_{1}) &= f'_{k}\left( \textstyle -\frac{2\sqrt{3}}{3} \right) \\[0.8em] &= 2k \cdot \left( -\frac{2\sqrt{3}}{3} \right)^{3} - 8k \cdot \left( -\frac{2\sqrt{3}}{3} \right) \\[0.8em] &= -\frac{48\sqrt{3}}{27}k + \frac{16\sqrt{3}}{3}k \\[0.8em] &= -\frac{48\sqrt{3}}{27}k + \frac{144\sqrt{3}}{27} \\[0.8em] &= \frac{96\sqrt{3}}{27}k \\[0.8em] &= \frac{32\sqrt{3}}{9}k \end{align*}\]
\[\begin{align*}f'_{k}(x_{2}) &= f'_{k}\left( \textstyle \frac{2\sqrt{3}}{3} \right) \\[0.8em] &= 2k \cdot \left( \frac{2\sqrt{3}}{3} \right)^{3} - 8k \cdot \frac{2\sqrt{3}}{3} \\[0.8em] &= \frac{48\sqrt{3}}{27}k - \frac{16\sqrt{3}}{3}k \\[0.8em] &= \frac{48\sqrt{3}}{27}k - \frac{144\sqrt{3}}{27} \\[0.8em] &= -\frac{96\sqrt{3}}{27}k \\[0.8em] &= -\frac{32\sqrt{3}}{9}k \end{align*}\]
\[\begin{align*}f'_{k}(x_{1}) &= -\frac{1}{f'_{k}(x_{2})} \\[0.8em] f'_{k}\left( \textstyle -\frac{2\sqrt{3}}{3} \right) &= -\frac{1}{f'_{k}\left( \textstyle \frac{2\sqrt{3}}{3} \right)} \\[0.8em] \frac{32\sqrt{3}}{9}k &= -\frac{1}{-\frac{32\sqrt{3}}{9}}k & &| \cdot \frac{32\sqrt{3}}{9}k \\[0.8em] \left( \frac{32\sqrt{3}}{9} \right)^{2} &= 1 \\[0.8em] \frac{1024 \cdot \cancel{3}}{27 \cancel{81}}k^{2} &= 1 & &| \cdot \frac{27}{1024} \\[0.8em] k^{2} &= \frac{27}{1024} & &| \; \sqrt{\quad} \enspace (k > 0) \\[0.8em] k &= \frac{3\sqrt{3}}{32} \\[0.8em] k &\approx 0{,}16 \end{align*}\]
Für \(k = \frac{3\sqrt{3}}{32}\) besitzt der zugehörige Graph der Funktionenschar \(f_{k}\) an den Wendestellen \(x_{1} = -\frac{2\sqrt{3}}{3}\) und \(x_{2} = \frac{2\sqrt{3}}{3}\) zwei zueinander senkrechte Wendetangenten.
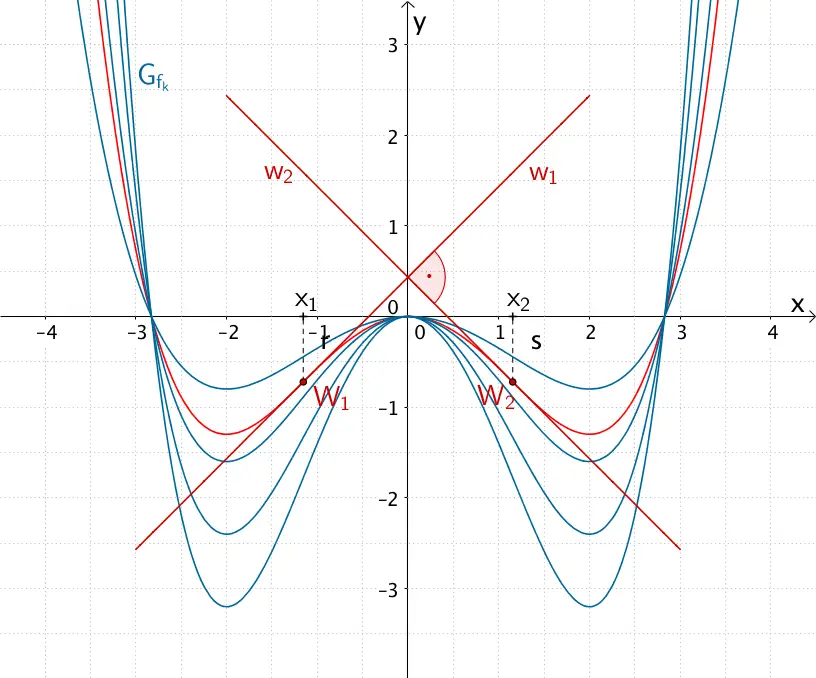
Kurvenschar \(G_{f_{k}}\) der in \(\mathbb R\) definierten Funktionenschar \(f_{k} \colon x \mapsto 0{,}5kx^{4} - 4kx^{2}\) mit \(k > 0\) sowie Graph der Scharfunktion für \(k = \frac{3\sqrt{3}}{32}\) mit den orthogonalen Wendetangenten \(w_{1}\) und \(w_{2}\) an den Wendestellen \(x_{1} = -\frac{2\sqrt{3}}{3}\) und \(x_{2} = \frac{2\sqrt{3}}{3}\)

