Bei der Herstellung wiederaufladbarer Batterien treten zwei Fehler auf.
\(A\): Die Abmessung der Batterie weicht von der Typennorm ab.
\(L\): Die Ladekapazität der Batterie liegt 20 % unter dem Sollwert.
Laut Qualitätskontrolle weisen 15 % der Batterien den Fehler \(L\) auf und 5 % den Fehler \(A\). Die Wahrscheinlichkeit, dass mindestens einer der beiden Fehler auftritt, wird mit 17 % angegeben.
a) Beschreiben Sie folgende Ereignisse im Sachzusammenhang:
α) \(\overline{\overline{A} \cap \overline{L}}\)
β) \((A \cap \overline{L}) \cup (\overline{A} \cap L)\)
b) Erstellen Sie eine den Sachverhalt beschreibende vollständig ausgefüllte Vierfeldertaffel.
c) Zeigen Sie dass die Ereignisse \(A\) und \(L\) stochastisch abhängig sind.
d) Erstellen Sie ein vollständig ausgefülltes Baumdiagramm, beginnend mit dem Ereignis \(A\). Beschreiben Sie, woran sich die stochastische Abhängigkeit der Ereignisse \(A\) und \(L\) an diesem Baumdiagramm erkennen lässt.
a) α) Beschreibung des Ereignisses \(\overline{\overline{A} \cap \overline{L}}\) im Sachzusammenhang
Das Ereignis \(\overline{A} \cap \overline{L}\) bedeutet: „Die wiederaufladbare Batterie ist fehlerfrei."
Dann bedeutet das Ereignis \(\overline{\overline{A} \cap \overline{L}}\): „Die wiederaufladbare Batterie ist nicht fehlerfrei." bzw. „Die wiederaufladbare Batterie weist mindestens einen der beiden Fehler \(A\) oder \(L\) auf."
Als Alternative wendet man eines der Gesetze von de Morgan an (vgl. Abiturskript - 3.1.1 Ereignisse):
Gesetze von de Morgan
Weder Ereignis \(A\) noch Ereignis \(B\); Keines der beiden Ereignisse
\[\overline{A} \cap \overline{B} = \overline{A \cup B}\]
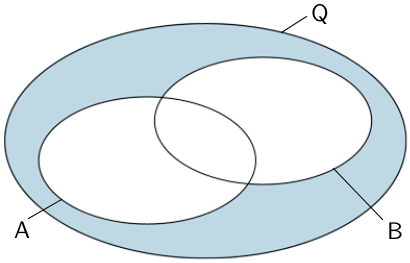
Nicht beide Ereignisse \(A\) und \(B\) zugleich; Höchstens eines der beiden Ereignisse
\[\overline{A \cap B} = \overline{A} \cup \overline{B}\]
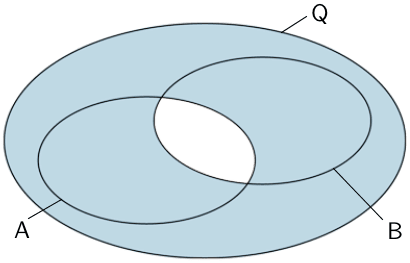
\[\begin{align*}\overline{\overline{A} \cap \overline{L}} &= A \cup L \\[0.8em] &= (A \cap \overline{L}) \cup (\overline{A} \cap L) \cup (A \cap L) \end{align*}\]
Das Ereignis \(\overline{\overline{A} \cap \overline{L}}\) beschreibt also die Vereinigungsmenge \(A \cup L\) und bedeutet: „Entweder weicht die Abmessung der wiederaufladbaren Batterie von der Typennorm ab, oder die Ladekapazität liegt unter dem Sollwert, oder die Batterie weist beide Fehler zugleich auf."
Also in Kurzform: „Die wiederaufladbare Batterie ist nicht fehlerfrei." bzw. „Die wiederaufladbare Batterie weist mindestens einen der beiden Fehler \(A\) oder \(L\) auf."
a) β) Beschreibung des Ereignisses \((A \cap \overline{L}) \cup (\overline{A} \cap L)\) im Sachzusammenhang
Das Ereignis \(A \cap \overline{L}\) bedeutet: „Die Abmessung der wiederaufladbaren Batterie weicht von der Typennorm ab, während die Ladekapazität dem Sollwert entspricht."
Das Ereignis \(\overline{A} \cap L\) bedeutet: „Die Ladekapazität der wiederaufladbaren Batterie liegt unter dem Sollwert, während die Abmessung der Batterie der Typennorm entspricht.
Das Ereignis \((A \cap \overline{L}) \cup (\overline{A} \cap L)\) bedeutet somit: „Entweder weicht die Abmessung der wiederaufladbaren Batterie von der Typennorm ab, oder die Ladekapazität der Batterie liegt unter dem Sollwert."
b) Vollständig ausgefüllte Vierfeldertaffel
(vgl. Abiturskript - 3.1.4 Baumdiagramm und Vierfeldertafel)
Gegeben sind folgende Wahrscheinlichkeiten:
\(P(L) = 0{,}15\), \(P(A) = 0{,}05\), \(P(A \cup L) = 0{,}17\)
| \(A\) | \(\overline{A}\) | ||
| \(L\) | \(0{,}15\) | ||
| \(\overline{L}\) | |||
| \(0{,}05\) | \(1\) |
Vierfeldertafel mit den Eintragungen der Wahrscheinlichkeiten \(P(L) = 0{,}15\) und \(P(A) = 0{,}05\)
Die Wahrscheinlichkeit der Vereinigungsenge \(A \cup L\) kann nicht in die Vierfelder eingetragen werden. Stattdessen wird mithilfe des Additionssatzes die Wahrscheinlichkeit der Schnittmenge \(A \cap L\) berechnet.
Additionssatz
Für zwei beliebige Ereignisse \(A\) und \(B\) gilt:
\[P(A \cup B) = P(A) + P(B) - P(A \cap B)\]
\[\begin{align*}P(A \cup L) &= P(A) + P(L) - P(A \cap L) &&| + P(A \cap L) - P(A \cup L) \\[0.8em] P(A \cap L) &= P(A) + P(L) - P(A \cup L) \\[0.8em] &= 0{,}05 + 0{,}15 - 0{,}17 \\[0.8em] &= 0{,}03 \end{align*}\]
| \(A\) | \(\overline{A}\) | ||
| \(L\) | \(\mathbf{\textcolor{#e74c3c}{0{,}03}}\) | \(0{,}15\) | |
| \(\overline{L}\) | |||
| \(0{,}05\) | \(1\) |
Vierfeldertafel, ergänzt um die Eintragung der Wahrscheinlichkeit \(P(A \cap L) = 0{,}03\)
Nun kann die Vierfeldertafel zeilen- bzw. spaltenweise durch Subtraktion (und ggf. Addition) vervollständigt werden, beispielsweise wie folgt:
\[P(\overline{A}) = 1 - P(A) = 1 - 0{,}05 = 0{,}95\]
\[P(\overline{L}) = 1 - P(L) = 1 - 0{,}15 = 0{,}85\]
\[P(\overline{A} \cap L) = P(L) - P(A \cap L) = 0{,}15 - 0{,}03 = 0{,}12\]
\[P(A \cap \overline{L}) = P(A) - P(A \cap L) = 0{,}05 - 0{,}03 = 0{,}02\]
\[P(\overline{A} \cap P(\overline{L})) = P(\overline{A}) - P(\overline{A} \cap L) = 0{,}95 - 0{,}12 = 0{,}83\]
| \(A\) | \(\overline{A}\) | ||
| \(L\) | \(0{,}03\) | \(\mathbf{\textcolor{#e74c3c}{0{,}12}}\) | \(0{,}15\) |
| \(\overline{L}\) | \(\mathbf{\textcolor{#e74c3c}{0{,}02}}\) | \(\mathbf{\textcolor{#e74c3c}{0{,}83}}\) | \(\mathbf{\textcolor{#e74c3c}{0{,}85}}\) |
| \(0{,}05\) | \(\mathbf{\textcolor{#e74c3c}{0{,}95}}\) | \(1\) |
Durch zeilen- bzw. spaltenweise Subtraktion vollständig ausgefüllte Vierfeldertafel
c) Nachweis, dass die Ereignisse \(A\) und \(L\) stochastisch abhängig sind
Es ist beispielsweise nachzuweisen, dass \(P(A \cap L) \neq P(A) \cdot P(L)\) gilt (vgl. Abiturskript - 3.1.6 Unabhängigkeit von Ereignissen).
Stochastische (Un)Abhängigkeit von zwei Ereignissen
Zwei Ereignisse \(A\) und \(B\) heißen stochastisch unabhängig, wenn
\(P(A) \cdot P(B) = P(A \cap B)\) gilt. (vgl. Merkhilfe) *
Andernfalls heißen die Ereignisse \(A\) und \(B\) stochastisch abhängig.
Sind zwei Ereignisse \(A\) und \(B\) stochastisch unabhängig, beeinflusst das Eintreten des Ereignisses \(A\) nicht das Eintreten des Ereignisses \(B\) und umgekehrt.
* Oder wenn
\(P(\overline{A}) \cdot P(B) = P(\overline{A} \cap B)\) bzw.
\(P(A) \cdot P(\overline{B}) = P(A \cap \overline{B})\) bzw.
\(P(\overline{A}) \cdot P(\overline{B}) = P(\overline{A} \cap \overline{B})\) gilt.
Der Angabe bzw. der Vierfeldertafel sind die Wahrscheinlichkeiten \(P(A) = 0{,}05\), \(P(L) = 0{,}15\) und \(P(A \cap L) = 0{,}03\) zu entnehmen.
\[P(A) \cdot P(L) = 0{,}05 \cdot 0{,}15 = 0{,}0075\]
\[\Longrightarrow \quad P(A \cap L) \neq P(A) \cdot P(L)\]
Also sind die Ereignisse \(A\) und \(L\) stochastisch abhängig.
d) Vollständig ausgefülltes Baumdiagramm, beginnend mit dem Ereignis \(A\) sowie Beschreibung, woran die stochastische Abhängigkeit der Ereignisse \(A\) und \(L\) zu erkennen ist
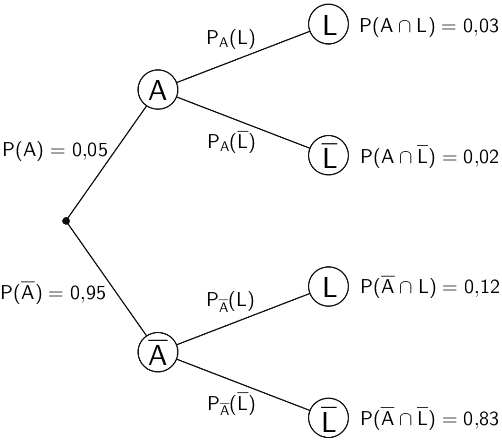
Baumdiagramm beginnend mit dem Ereignis \(A\) und den Eintragungen der aus der Vierfeldertafel bekannten Wahrscheinlichkeiten
Die bedingten Wahrscheinlichkeiten an den zweiten Ästen des Baumdiagramms lassen sich wie folgt berechnen (vgl. Abiturskript - Bedingte Wahrscheinlichkeit):
Bedingte Wahrscheinlichkeit
Die Wahrscheinlichkeit für das Eintreten des Ereignisses \(B\) unter der Voraussetzung oder der Bedingung, dass das Ereignis \(A\) bereits eingetreten ist, heißt bedingte Wahrscheinlichkeit von \(\boldsymbol{B}\) unter der Bedingung \(\boldsymbol{A}\) und wird durch die Schreibweise \(P_{A}(B)\) gekennzeichnet.
Es gilt: \(P_{A}(B) = \dfrac{P(A \cap B)}{P(A)} \quad (P(A) \neq 0)\)
(vgl. Merkhilfe)
\[P_{A}(L) = \frac{P(A \cap L)}{P(A)} = \frac{0{,}03}{0{,}05} = 0{,}6\]
\[P_{\overline{A}}(L) = \frac{P(\overline{A} \cap L)}{P(\overline{A})} = \frac{0{,}12}{0{,}95} = \frac{12}{95}\]
Nach der Knotenregel gilt:
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
\[P_{A}(\overline{L}) = 1 - P_{A}(L) = 1 - 0{,}6 = 0{,}4\]
\[P_{\overline{A}}(\overline{L}) = 1 - P_{\overline{A}}(L) = 1 - \frac{12}{95} = \frac{83}{95}\]
Als Alternative können die bedingten Wahrscheinlichkeiten auch mithilfe der Vierfeldertafel berechnet werden. Sie ergeben sich zeilen- bzw. spaltenweise als Quotient aus dem Eintrags einer inneren Zelle und dem Eintrag der Randzelle.
| \(A\) | \(\overline{A}\) | ||
| \(L\) | \(0{,}03\) | \(0{,}12\) | \(0{,}15\) |
| \(\overline{L}\) | \(0{,}02\) | \(0{,}83\) | \(0{,}85\) |
| \(0{,}05\) | \(0{,}95\) | \(1\) |
\[P_{A}(L) = \frac{0{,}03}{0{,}05} = 0{,}6\]
\[P_{A}(\overline{L}) = \frac{0{,}02}{0{,}05} = 0{,}4\]
\[P_{\overline{A}}(L) = \frac{0{,}12}{0{,}95} = \frac{12}{95}\]
\[P_{\overline{A}}(\overline{L}) = \frac{0{,}83}{0{,}95} = \frac{83}{95}\]
Somit ergibt sich folgendes vollständig ausgefülltes Baumdiagramm:
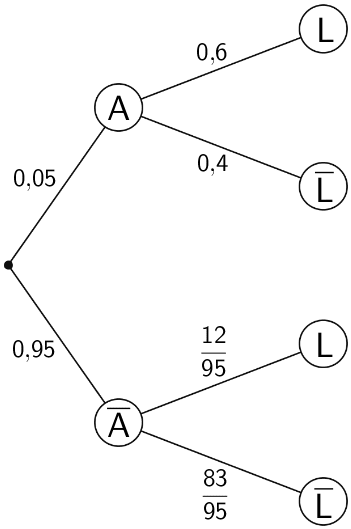
Vollständig ausgefülltes Baumdiagramm beginnend mit dem Ereignis \(A\)
Die stochastische Abhängigkeit der Ereignisse \(A\) und \(L\) ist an den verschiedenen bedingten Wahrscheinlichkeiten der zweiten Äste des Baumdiagramms zu erkennen, den es gilt:
\[0{,}6 \neq \frac{12}{95}\]
\[0{,}4 \neq \frac{83}{95}\]
Im Falle der stochastischen Unabhängigkeit der Ereignisse \(A\) und \(L\) würde beispielsweise \(P_{A}(L) = P_{\overline{A}}(L) = P(L)\) gelten.

