Gegeben ist die Funktion \(f \colon x \mapsto \frac{1}{2}x \cdot e^{1 - x}\). Der Graph der Funktion \(f\) wird mit \(G_{f}\) bezeichnet.
a) Untersuchen Sie die Funktion \(f\) auf Nullstellen und bestimmen Sie das Verhalten von \(f\) an den Rändern des Definitionsbereichs.
b) Berechnen Sie die Lage und die Art der Extrempunkte von \(G_{f}\).
(zur Kontrolle: \(f'(x) = \frac{1}{2}e^{1 - x}(1 - x)\))
c) Untersuchen Sie das Krümmungsverhalten von \(G_{f}\) und geben Sie die Koordinaten des Wendepunkts an. Bestimmen Sie die Gleichung der Wendetangente \(w\).
(zur Kontrolle: \(f''(x) = \frac{1}{2}e^{1 - x}(x - 2)\))
d) Skizzieren Sie \(G_{f}\) sowie die Wendetangente \(w\) unter Berücksichtigung der bisherigen Ergebnisse in ein geeignetes Koordinatensystem.
e) Weisen Sie nach, dass die Funktion \(F\colon x \mapsto -\frac{1}{2}e^{1 - x}(x + 1)\) eine Stammfunktion der Funktion \(f\) ist.
f) Der Graph \(G_{f}\) und die Wendetangente \(w\) schließen im ersten Quadranten ein Flächenstück mit dem Flächeninhalt \(A\) ein. Schraffieren Sie dieses Flächenstück in der Skizze aus Teilaufgabe d und berechnen Sie den Flächeninhalt \(A\).
g) Berechnen Sie das Integral \(\displaystyle \int_{0}^{+\infty} f(x) dx\) und geben Sie die geometrische Bedeutung des Ergebnisses an.
a) Nullstellen und Verhalten an den Rändern des Definitionsbereichs von \(f\)
\[f(x) = \frac{1}{2}x \cdot e^{1 - x}\]
Nullstelle(n) der Funktion \(f\)
\[\begin{align*}f(x) &= 0 \\[0.8em] \frac{1}{2}x \cdot \underbrace{e^{1 - x}}_{>\,0} &= 0 \end{align*}\]
Nullstelle(n) einer Funktion bestimmen
Eine Nullstelle ist die \(x\)-Koordinate eines gemeinsamen Punktes des Graphen einer Funktion \(x \mapsto f(x)\) mit der \(x\)-Achse. An einer Nullstelle gilt: \(f(x) = 0\).

Satz vom Nullprodukt: Ein Produkt ist genau dann null, wenn einer der Faktoren null ist.
\(f(x) \cdot g(x) = 0 \enspace \Rightarrow \enspace f(x) = 0\) oder \(g(x) = 0\)
Ein Quotient von Funktionen ist genau dann null, wenn die Zählerfunktion null ist.
\(\dfrac{f(x)}{g(x)} = 0 \enspace \Rightarrow \enspace f(x) = 0\; (g(x) \neq 0)\)
Lösungsformel für quadratische Gleichungen (Mitternachtsformel, vgl. Merkhilfe)
\[\textcolor{#cc071e}{a}x^2 + \textcolor{#0087c1}{b}x + \textcolor{#e9b509}{c} = 0 \enspace \Leftrightarrow \enspace x_{1,2} = \frac{-\textcolor{#0087c1}{b} \pm \sqrt{\textcolor{#0087c1}{b}^2 - 4\textcolor{#cc071e}{a}\textcolor{#e9b509}{c}}}{2\textcolor{#cc071e}{a}}\]
Diskriminante \(D = b^2 -4ac \;\):
\(D < 0\,\): keine Lösung
\(D = 0\,\): genau eine Lösung
\(D > 0\,\): zwei verschiedene Lösungen
Folgende Fälle lassen sich einfacher durch Umformung lösen:
\[\begin{align*}\textcolor{#cc071e}{a}x^2 + \textcolor{#0087c1}{b}x &= 0 &&| \; x\; \text{ausklammern (Produkt formulieren)} \\[0.8em] x \cdot (ax + b) &= 0 \\[0.8em] \Rightarrow \enspace x = 0 \vee ax + b &= 0 \end{align*}\]
\[\begin{align*}\textcolor{#cc071e}{a}x^2 + \textcolor{#e9b509}{c} &= 0 &&| -c \enspace (c \neq 0) \\[0.8em] ax^2 &= -c &&| : a \\[0.8em] x^2 &= -\frac{c}{a} &&| \; \sqrt{\quad} \\[0.8em] x_{1,2} &= \pm \sqrt{-\frac{c}{a}} \end{align*}\]
Zwei Lösungen, falls \(-\dfrac{c}{a} > 0\), keine Lösung, falls \(-\dfrac{c}{a} < 0\)
Vorgehensweise für die Bestimmung der Nullstelle(n) einer ganzrationalen Funktion ab Grad 3:
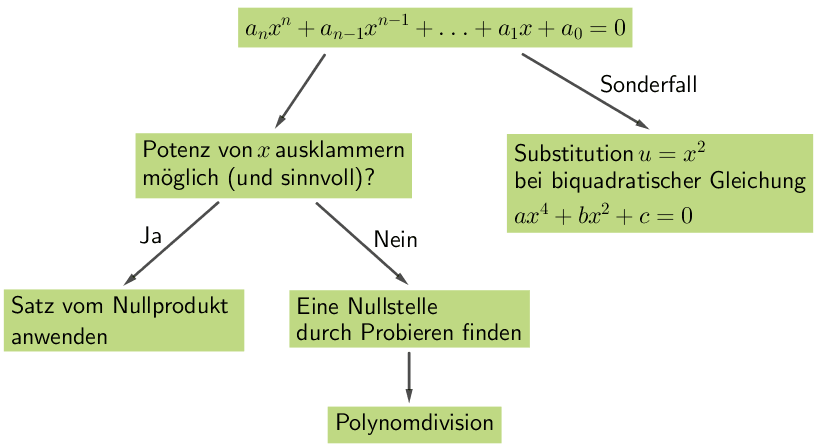
vgl. Abiturskript - 1.1.3 Ganzrationale Funktion, Nullstellen
Nullstellen einer gebrochenrationalen Funktion \(f(x) = \dfrac{\textcolor{#0087c1}{z(x)}}{n(x)}\) sind alle Nullstellen des Zählerpolynoms \(\textcolor{#0087c1}{z(x)}\), die nicht zugleich Nullstellen des Nennerpolynoms \(\boldsymbol{n(x)}\) sind.
Ist \(x_0\) eine Nullstelle des Zählerpolynoms \(\boldsymbol{z(x)}\) und zugleich eine vollständig kürzbare Nullstelle des Nennerpolynoms \(\boldsymbol{n(x)}\), so besitzt die gebrochenrationale Funktion \(f\) an der Stelle \(x_0\) eine hebbare Definitionslücke.
(vgl. Abiturskript - 1.2.1 Gebrochenrationale Funktion, Nullstellen und Polstellen)
Eine Wurzelfunktion \(f(x) = \sqrt{\textcolor{#cc071e}{g(x)}}\) nimmt genau dann den Wert null an, wenn der Radikand (Term unter der Wurzel) null ist.
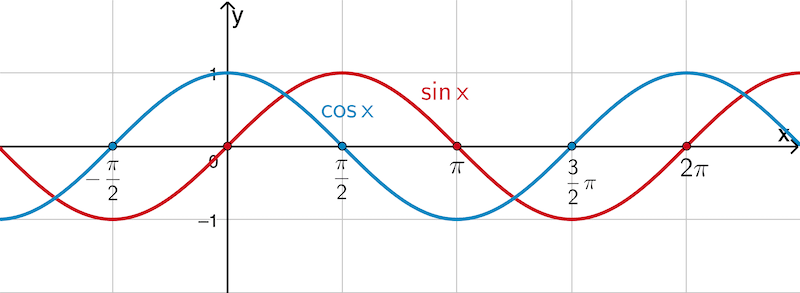
\[\sin{x} = 0 \enspace \Rightarrow \enspace x = k \cdot \pi \; (k \in \mathbb Z)\]
\[\cos{x} = 0 \enspace \Rightarrow \enspace x = \dfrac{\pi}{2} + k \cdot \pi \; (k \in \mathbb Z)\]
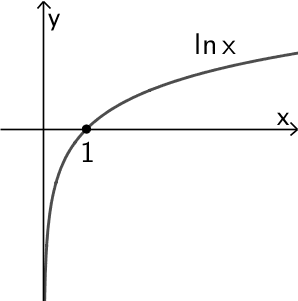
Die natürliche Logarithmusfunktion \(x \mapsto \ln{x}\) besitzt die einzige Nullstelle \(\boldsymbol{x = 1}\).
\[\ln{\left( \textcolor{#0087c1}{f(x)} \right)} = 0 \enspace \Rightarrow \enspace \textcolor{#0087c1}{f(x) = 1}\]
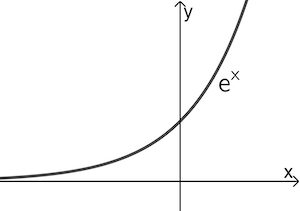
Die natürliche Exponentialfunktion \(x \mapsto e^x\) sowie jede verkettete Funktion \(x \mapsto e^{f(x)}\) besitzt keine Nullstelle!
Satz vom Nullprodukt:
Ein Produkt ist gleich Null, wenn mindestens einer der Faktoren gleich Null ist.
Der natürliche Exponentialterm \(e^{1 - x}\) ist für \(x \in \mathbb R\) stets größer als Null (vgl. Abiturskript - 1.3.1 Eigenschaften und Rechenregeln, Natürliche Exponential- und Logarithmusfunktion).
Es verbleibt \(x = 0\) als einzige Nullstelle der Funktion \(f\).
Verhalten von \(f\) an den Rändern des Definitionsbereichs
Weder der lineare Term \(\frac{1}{2}x\) noch der natürliche Exponentialterm \(e^{1 - x}\) schränkt den Definitionsbereich von \(f\) ein. Die Funktion \(f\) ist also in \(\mathbb R\) definiert und es ist das Verhalten von \(f\) für \(x \to -\infty\) bzw. \(x \to +\infty\) zu untersuchen.
\[D_{f} = \mathbb R = \; ]-\infty;+\infty[\]
\[\lim \limits_{x\,\to\,-\infty} f(x) = \lim \limits_{x\,\to\,-\infty} \underbrace{\frac{1}{2}x}_{\to\,-\infty} \cdot \underbrace{e^{1 - x}}_{\to\,+\infty} = -\infty\]
Wichtiger Grenzwert
\[\lim \limits_{x \, \to \, +\infty} \frac{x^r}{e^x} = 0 \enspace (r > 0)\]
Für \(\,x \to +\infty\,\) wächst \(e^x\) „schneller" als jede Potenz \(x^r \enspace (r > 0)\).
(vgl. Merkhilfe)
\[\begin{align*} \lim \limits_{x\,\to\,+\infty} f(x) &= \lim \limits_{x\,\to\,+\infty} \underbrace{\frac{1}{2}x}_{\to\,+\infty} \cdot \underbrace{e^{1 - x}}_{\to\,0} & &| \; a^{-n} = \frac{1}{a^{n}}; \; \text{hier:}\; e^{-(x - 1)} = \frac{1}{e^{x - 1}} \\[0.8em] &= \lim \limits_{x\,\to\,+\infty} \frac{\overbrace{\frac{1}{2}x}^{\to\,+\infty}}{\underbrace{e^{x - 1}}_{\to\,+\infty}} \\[0.8em] &= 0 \end{align*}\]
Unter Berücksichtigung des wichtigen Grenzwerts \(\lim \limits_{x\,\to\,+\infty} \dfrac{x^{r}}{e^{x}} = 0; \;(r > 0)\) ergibt sich \(\lim \limits_{x\,\to\,+\infty} f(x) = 0\). Der natürliche Exponentialterm \(e^{x - 1}\) wächst für \(x \to +\infty\) „schneller" als der lineare Term \(\frac{1}{2}x\).
b) Lage und die Art der Extrempunkte von \(G_{f}\)
Die notwendige Bedingung für einen Extrempunkt von \(G_{f}\) lautet (vgl. Abiturskript - 1.5.3 Monotonieverhalten, Extrem- und Terrassenpunkte):
Anwendung der Differentialrechnung:
Extrempunkte
Ist \(f'(x_{0}) = 0\) und wechselt \(f'\) an der Stelle \(x_{0}\) das Vorzeichen, so hat \(G_{f}\) an der Stelle \(x_{0}\) einen Extrempunkt.
(vgl. Merkhilfe)
\[f'(x) = 0\]
Erste Ableitung \(f'\) von \(f\) bilden:
Die Funktion \(f\) lässt sich mithilfe der Produktregel und der Kettenregel sowie der Ableitung der natürlichen Exponentialfunktion bzw. einer Potenzfunktion ableiten. Für die anschließende Untersuchung der Nullstellen von \(f'\) ist es zweckmäßig, den Funktionsterm \(f'(x)\) als Produkt zu formulieren (Ausklammern des Exponentialterms).
\[f(x) = \frac{1}{2}x \cdot e^{1 - x}; \; D_{f} = \mathbb R\]
Ableitung einer Potenzfunktion
\[ f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Ableitung der natürlichen Exponentialfunktion
\[ f(x) = e^x \quad \Longrightarrow \quad f'(x) = e^x\]
Produktregel
\[f(x) = u(x) \cdot v(x) \quad \Longrightarrow \quad f'(x) = u'(x) \cdot v(x) + u(x) \cdot v'(x)\]
Kettenregel
\[ f(x) = u(v(x)) \quad \Longrightarrow \quad f'(x) = u'(v(x)) \cdot v'(x) \]
(vgl. Merkhilfe)
\[\begin{align*} f'(x) &= \frac{1}{2} \cdot e^{1 - x} + \frac{1}{2}x \cdot e^{1 - x} \cdot (-1) \\[0.8em] &= \frac{1}{2}e^{1 - x} - \frac{1}{2}xe^{1 - x} & &| \; \frac{1}{2}e^{1 - x} \; \text{ausklammern} \\[0.8em] &= \frac{1}{2}e^{1 - x}(1 - x) \end{align*}\]
Nullstelle von \(f'\) bestimmen:
\[f'(x) = \underbrace{\frac{1}{2}e^{1 - x}}_{>\,0}(1 - x)\]
Da der natürliche Exponentialterm \(\frac{1}{2}e^{1 - x}\) für \(x \in \mathbb R\) stets größer als Null ist (vgl. Abiturskript - 1.3.1 Eigenschaften und Rechenregeln, Natürliche Exponential- und Logarithmusfunktion), besitzt \(f'(x)\) die einzige Nullstelle \(x = 1\).
\[\begin{align*}f'(x) = 0 \quad \Longrightarrow \quad 1 - x &= 0 & &| + 1 \\[0.8em] 1 = x \end{align*}\]
An der Stelle \(x = 1\) besitzt der Graph der Funktion \(f\) eine waagrechte Tangente, welche auf einen Extrempunkt hinweist. Die in Teilaufgabe a ermittelten Grenzwerte \(\lim \limits_{x\,\to\,-\infty} f(x) = -\infty\) und \(\lim \limits_{x\,\to\,+\infty } f(x) = 0\) bestätigen den Hinweis und deuten auf ein globales Maximum von \(f\) an der Stelle \(x = 1\) hin.
Art des Extrempunkts nachweisen:
Da in Teilaufgabe c für die Bestimmung des Krümmungsverhaltens die zweite Ableitung \(f''\) benötigt wird, ist es sinnvoll, den Nachweis der Art des Extrempunkts mithilfe von \(f''(1)\) zu führen. Ein Nachweis mithilfe des Monotoniekriteriums (einer Monotonietabelle) ist ebenso möglich.
1. Möglichkeit: Nachweis der Art des Extrempunkts mithilfe der zweiten Ableitung
Anwendung der Differentialrechnung:
Art von Extrempunkten mithilfe der zweiten Ableitung nachweisen
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) > 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Minimum (Tiefpunkt).
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) < 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Maximum (Hochpunkt).
Zweite Ableitung \(f''\) von \(f\) bilden:
Die zweite Ableitung \(f''\) wird wiederum mithilfe der Produktregel und der Kettenregel sowie der Ableitung der natürlichen Exponentialfunktion bzw. einer Potenzfunktion gebildet.
\[f'(x) = \frac{1}{2}e^{1 - x}(1 - x)\]
Ableitung einer Potenzfunktion
\[ f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Ableitung der natürlichen Exponentialfunktion
\[ f(x) = e^x \quad \Longrightarrow \quad f'(x) = e^x\]
Produktregel
\[f(x) = u(x) \cdot v(x) \quad \Longrightarrow \quad f'(x) = u'(x) \cdot v(x) + u(x) \cdot v'(x)\]
Kettenregel
\[ f(x) = u(v(x)) \quad \Longrightarrow \quad f'(x) = u'(v(x)) \cdot v'(x) \]
(vgl. Merkhilfe)
\[\begin{align*} f''(x) &= \frac{1}{2}e^{1 - x} \cdot (-1) \cdot (1 - x) + \frac{1}{2}e^{1 - x} \cdot (-1) \\[0.8em] &= \frac{1}{2}e^{1 - x} (x - 1) - \frac{1}{2}e^{1 - x} & &| \; \frac{1}{2}e^{1 - x} \; \text{ausklammern} \\[0.8em] &= \frac{1}{2}e^{1 - x}(x - 2) \end{align*}\]
Das Vorzeichen des Funktionswerts \(f''(1)\) bestimmt die Art des Extrempunkts von \(G_{f}\) an der Stelle \(x = 1\).
Anwendung der Differentialrechnung:
Art von Extrempunkten mithilfe der zweiten Ableitung nachweisen
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) > 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Minimum (Tiefpunkt).
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) < 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Maximum (Hochpunkt).
\[f''(1) = \frac{1}{2}e^{1 - 1}(1 - 2) = \frac{1}{2} \cdot 1 \cdot (-1) = -\frac{1}{2}\]
\[\left. \begin{align*} &f'(1) = 0 \\[0.8em] &f''(1) < 0 \end{align*} \right\}\enspace \Rightarrow \enspace \text{Hochpunkt}\;HoP(1|f(1))\]
2. Möglichkeit: Nachweis der Art des Extrempunkt mithilfe des Monotoniekriteriums bzw. einer Monotonietabelle
Anwendung der Differetialrechnung:
Monotoniekriterium
\(f'(x) < 0\) im Intervall \( I \enspace \Rightarrow \enspace G_{f}\) fällt streng monoton in \(I\)
\(f'(x) > 0\) im Intervall \( I \enspace \Rightarrow \enspace G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
\[f'(x) = \underbrace{\frac{1}{2}e^{1 - x}}_{>\,0}(1 - x)\]
Der Faktor \((1 - x)\) bestimmt den Vorzeichenwechsel von \(f'\) und damit das Monotonieverhalten in der Umgebung der Stelle \(x = 1\).
\[\left. \begin{align*}&f'(x) > 0 \; \text{für} \; x < 1 \\[0.8em] &f'(1) = 0 \\[0.8em] &f'(x) < 0 \; \text{für} \; x > 1 \end{align*} \right\}\enspace \Rightarrow \enspace \text{Hochpunkt}\;HoP(1|f(1))\]
Veranschaulichung mit einer Monotonietabelle:
| \(x\) | \(x < 1\) | \(x = 1\) | \(x > 1\) |
| \(\frac{1}{2}e^{x - 1}\) | \(+\) | \(+\) | \(+\) |
| \((1 - x)\) | \(+\) | \(0\) | \(-\) |
| \(f'(x)\) | \(+\) | \(0\) | \(-\) |
| \(G_{f}\) | \(\nearrow\) | \(HoP(1|f(1))\) | \(\searrow\) |
\(y\)-Koordinate des Hochpunkts berechnen:
\[f(x) = \frac{1}{2}x \cdot e^{1 - x}; \; D_{f} = \mathbb R\]
\[f(1) = \frac{1}{2} \cdot 1 \cdot e^{1 - 1} = \frac{1}{2}\]
\[\Longrightarrow \quad HoP\Big(1\Big| \textstyle{\frac{1}{2}}\Big)\]
c) Krümmungsverhalten von \(G_{f}\), Koordinaten des Wendepunkts und Gleichung der Wendetangente \(w\)
Krümmungsverhalten von \(G_{f}\) und Koordinaten des Wendepunkts
(vgl. Abiturskript - 1.5.4 Krümmungsverhalten und Wendepunkte)
Anwendung der Differentialrechnung:
Krümmungsverhalten von Funktionsgraphen
\(f''(x) < 0\) im Intervall \(I \quad \Longrightarrow \quad G_f\) ist in \(I\) rechtsgekrümmt.
\(f''(x) > 0\) im Intervall \(I \quad \Longrightarrow \quad G_f\) ist in \(I\) linksgekrümmt.
(vgl. Merkhilfe)
Die zweite Ableitung \(f''\) von \(f\) ist aus Teilaufgabe b bereits bekannt.
\[f''(x) = \underbrace{\frac{1}{2}e^{1 - x}}_{> \, 0}(x - 2)\]
Der Faktor \((x - 2)\) bestimmt den Vorzeichenwechsel von \(f''(x)\).
Für \(x < 2\) gilt \(f''(x) < 0\). Folglich ist \(G_{f}\) für \(x < 2\) rechtsgekrümmt.
Für \(x > 2\) gilt \(f''(x) > 0\). Folglich ist \(G_{f}\) für \(x > 2\) linksgekrümmt.
Zudem gilt \(f''(2) = 0\). Da \(f''\) in der Umgebung der Stelle \(x = 2\) das Vorzeichen wechselt, hat \(G_{f}\) an der Stelle \(x = 2\) einen Wendepunkt.
Anwendung der Differetialrechnung:
Wendepunkt
Ist \(f''(x_0) = 0\) und wechselt \(f''\) an der Stelle \(x_0\) das Vorzeichen, so hat \(G_f\) an der Stelle \(x_0\) einen Wendepunkt.
(vgl. Merkhilfe)
Alternative:
Es muss \(f''(x_{0}) = 0\) und \(f'''(x_{0}) \neq 0\) gelten.
\[\left. \begin{align*}&f''(x) < 0 \; \text{für} \; x < 2 \\[0.8em] &f''(2) = 0 \\[0.8em] &f''(x) > 0 \; \text{für} \; x > 2 \end{align*} \right\}\enspace \Rightarrow \enspace \text{Wendepunkt}\;W(2|f(2))\]
Veranschaulichung mit einer Krümmungstabelle:
| \(x\) | \(x < 2\) | \(x = 2\) | \(x > 2\) |
| \(\frac{1}{2}e^{x - 1}\) | \(+\) | \(+\) | \(+\) |
| \((x - 2)\) | \(-\) | \(0\) | \(+\) |
| \(f''(x)\) | \(-\) | \(0\) | \(+\) |
| \(G_{f}\) | \(\Large \curvearrowright\) | \(W(2|f(2))\) | \(\style{display: inline-block; transform:rotate(0.5turn);}{\Large \curvearrowleft}\) |
\(y\)-Koordinate des Wendepunkts berechnen:
\[f(x) = \frac{1}{2}x \cdot e^{1 - x}; \; D_{f} = \mathbb R\]
\[f(2) = \frac{1}{2} \cdot 2 \cdot e^{1 - 2} = e^{-1} = \frac{1}{e}\]
\[\Longrightarrow \quad W\Big(2\Big| \textstyle{\frac{1}{e}}\Big)\]
Gleichung der Wendetangente \(w\)
Der Ansatz für die Gleichung der Wendetangente \(w\) kann mit der allgemeinen Geradengleichung oder mit der Tangentengleichung erfolgen.
1. Lösungsansatz: Allgemeine Geradengleichung
Allgemeine Geradengleichung
\[y = mx + t\]
Wobei \(m\) die Steigung und \(t\) der \(y\)-Achsenabschnitt der Geraden ist.
\[w \colon y = m_{w} \cdot x + t\]
Die erste Ableitung \(f'\) an der Wendestelle \(x = 2\) beschreibt die Steigung \(m_{w}\) der Wendetangente \(w\).
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
\(f'(x) = \frac{1}{2}e^{1 - x}(1 - x)\) (vgl. Teilaufgabe b)
\[\begin{align*} m_{w} &= f'(2) \\[0.8em] &= \frac{1}{2}e^{1 - 2}(1 - 2) \\[0.8em] &= -\frac{1}{2}e^{-1} & &| \; a^{-n} = \frac{1}{a^{n}} \\[0.8em] &= -\frac{1}{2e} \end{align*}\]
Damit ergibt sich die Gleichung der Wendetangente \(w\) zu:
\[w \colon y = -\frac{1}{2e}x + t\]
\(y\)-Achsenabschnitt \(t\) bestimmen:
Die Wendetangente \(w\) verläuft durch den Wendepunkt \(W\Big(2\Big| \textstyle{\frac{1}{e}}\Big)\). Setz man die Koordinaten von \(W\) in die Gleichung der Wendetangente \(w\) ein, lässt sich damit der \(y\)-Achsenabschnitt \(t\) berechnen.
\[\begin{align*}W \in w\colon \frac{1}{e} &= -\frac{1}{2e} \cdot 2 + t \\[0.8em] \frac{1}{e} &= -\frac{1}{e} + t & &| + \frac{1}{e} \\[0.8em] \frac{2}{e} &= t \end{align*}\]
Gleichung der Wendetangente \(w\) angeben:
\[w \colon y = -\frac{1}{2e}x + \frac{2}{e}\]
2. Lösungsansatz: Tangentengleichung
Gleichung einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\;(x_0|f(x_0)) \):
\[y = f'(x_{0}) \cdot (x - x_{0}) + f(x_{0})\]
\(W\Big(2\Big| \textstyle{\frac{1}{e}}\Big)\)
\[w \colon y = f'(2) \cdot (x - 2) + f(2)\]
Mit \(f'(2) = -\frac{1}{2e}\) und \(f(2) = \frac{1}{e}\) (vgl. 1. Lösungsansatz) folgt:
\[\begin{align*}w \colon y &= f'(2) \cdot (x - 2) + f(2) \\[0.8em] &= -\frac{1}{2e} \cdot (x - 2) + \frac{1}{e} \\[0.8em] &= -\frac{1}{2e}x + \frac{1}{e} + \frac{1}{e} \\[0.8em] &= -\frac{1}{2e}x + \frac{2}{e} \end{align*}\]
d) Skizze von \(G_{f}\) und der Wendetangente \(w\) unter Berücksichtigung der bisherigen Ergebnisse
Bisherige Ergebnisse:
- \(x = 0\) ist einzige Nullstelle von \(f\).
- \(\lim \limits_{x\,\to\,-\infty} f(x) = -\infty; \; \lim \limits_{x\,\to\,+\infty} f(x) = 0\)
- \(G_{f}\) besitzt den Hochpunkt \(HoP\Big(1\Big| \textstyle{\frac{1}{2}}\Big)\).
- \(G_{f}\) besitzt den Wendepunkt \(W\Big(2\Big| \textstyle{\frac{1}{e}}\Big)\).
- Die Gleichung der Wendetangente \(w\) lautet: \(w \colon y = -\frac{1}{2e}x + \frac{2}{e}\).
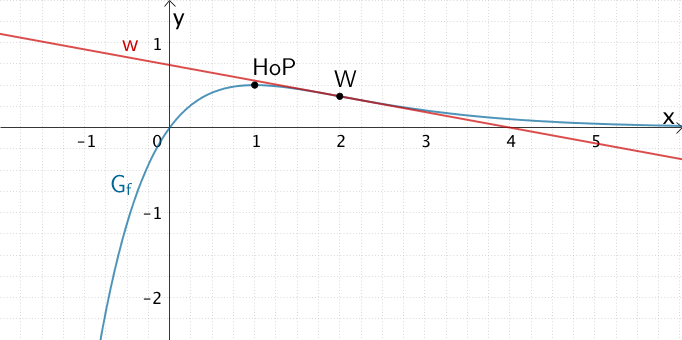
Graph \(G_{f}\) der Funktion \(f \colon x \mapsto \frac{1}{2}x \cdot e^{1 - x}\) mit Hochpunkt \(HoP\Big(1\Big| \textstyle{\frac{1}{2}}\Big)\), Wendepunkt \(W\Big(2\Big| \textstyle{\frac{1}{e}}\Big)\) und Wendetangente \(w \colon y = -\frac{1}{2e}x + \frac{2}{e}\)
e) Nachweis, dass die Funktion \(F\colon x \mapsto -\frac{1}{2}e^{1 - x}(x + 1)\) eine Stammfunktion von \(f\) ist
Gemäß der Definition einer Stammfunktion muss \(F'(x) = f(x)\) gelten.
Stammfunktion
Eine differenzierbare Funktion \(F(x)\) heißt eine Stammfunktion von \(f(x)\), wenn
\(F'(x) = f(x)\) mit \(D_{F} = D_{f}\)
gilt.
\(F(x) = -\frac{1}{2}e^{1 - x}(x + 1)\)
\(f(x) = \frac{1}{2}xe^{1 - x}; \; D_{f} = \mathbb R\)
Die Funktion \(F\) lässt sich unter Anwendung der Produktregel, der Kettenregel, der Summen- und der Faktorregel sowie der Ableitung der natürlichen Exponentialfunktion bzw. einer Potenzfunktion ableiten.
Produktregel
\[f(x) = u(x) \cdot v(x) \quad \Longrightarrow \quad f'(x) = u'(x) \cdot v(x) + u(x) \cdot v'(x)\]
Kettenregel
\[f(x) = u(v(x)) \quad \Longrightarrow \quad f'(x) = u'(v(x)) \cdot v'(x) \]
Ableitung der natürlichen Exponentialfunktion
\[ f(x) = e^x \quad \Longrightarrow \quad f'(x) = e^x\]
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Faktorregel
\(f(x) = a \cdot u(x) \quad \Longrightarrow \quad f'(x) = a \cdot u'(x)\)
Summenregel
\(f(x) = u(x) + v(x) \quad \Longrightarrow \quad f'(x) = u'(x) + v'(x)\)
(vgl. Merkhilfe)
\[\begin{align*}F'(x) &= -\frac{1}{2}\left[ e^{1 - x} \cdot (-1) \cdot (x + 1) + e^{1 - x} \cdot (1 + 0) \right]\\[0.8em] &= -\frac{1}{2}\left[ e^{1 - x} \cdot (-x - 1) + e^{1 - x} \right] & &| \; e^{1 - x} \; \text{ausklammern} \\[0.8em] &= -\frac{1}{2} \left( -x - 1 + 1 \right) \\[0.8em] &= -\frac{1}{2}e^{1 - x} \cdot (-x) \\[0.8em] &= \frac{1}{2}xe^{1 - x} \\[0.8em] &= f(x) \end{align*}\]
Also ist die Funktion \(F \colon x \mapsto -\dfrac{1}{2}e^{1 - x}(x + 1)\) eine Stammfunktion der Funktion \(f \colon x \mapsto \dfrac{1}{2}xe^{1 - x}\).
f) Schraffieren des Flächenstücks mit dem Flächeninhalt \(A\) und Berechnung des Flächeninhalts \(A\)
Schraffieren des Flächenstücks mit dem Flächeninhalt \(A\)
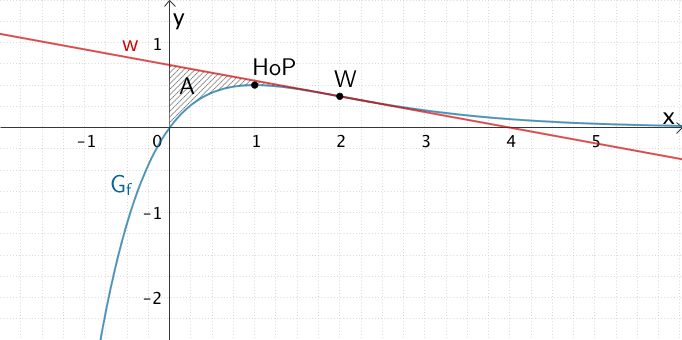
Flächenstück mit dem Flächeninhalt \(A\), das der Graph \(G_{f}\) und die Wendetangente \(w\) im ersten Quadranten einschließen.
Berechnung des Flächeninhalts \(A\)
1. Möglichkeit: Flächeninhalt eines Trapezes mit einbeziehen
![Flächenstücke, welche die Wendetangente w bzw. der Graph der Funktion f im Intervall [0;2] mit der x-Achse einschließen. Flächenstücke, welche die Wendetangente w bzw. der Graph der Funktion f im Intervall [0;2] mit der x-Achse einschließen.](/images/stories/Klausuren/Klausuren_Q12_1/Klausur_Q12_1-002/Klausur_Q12_1-002_A2_3.png)
Flächeninhalte der Flächenstücke, welche die Wendetangente \(w\) bzw. der Graph der Funktion \(f\) im Intervall \([0;2]\) mit der \(x\)-Achse einschließen.
Die Wendetangente \(w\) schneidet die \(y\)-Achse im Punkt \(\Big( 0 \Big| \textstyle \frac{2}{e} \Big)\) (vgl. Teilaufgabe c, \(y\)-Achsenabschnitt der Gleichung der Wendetangente). Der Wendepunkt \(W\Big(2\Big| \textstyle{\frac{1}{e}}\Big)\) ist gemeinsamer Punkt von \(G_{f}\) und der Wendetangente \(w\).
Der Flächeninhalt des Flächenstücks, das die Wendetangente im Intervall \([0;2]\) mit der \(x\)-Achse einschließt lässt sich mithilfe der Formel für den Flächeninhalt eines Trapezes berechnen.
Das bestimmte Integral \(\displaystyle \int_{0}^{2} f(x) dx\) errechnet die Maßzahl des Flächeninhalts des Flächenstücks, das \(G_{f}\) im Intervall \([0;2]\) mit der \(x\)-Achse einschließt.
Der gesuchte Flächeninhalt \(A\) lässt sich mithilfe der Differenz der beiden Flächeninhalte ermitteln.
\[A = A_{Trapez} - \int_{0}^{2} f(x) dx\]
Für die Berechnung des bestimmten Integrals \(\displaystyle \int_{0}^{2} f(x) dx\) wird die Stammfunktion \(F\) aus Teilaufgabe e verwendet.
\(F(x) = -\frac{1}{2}e^{1 - x}(x + 1)\)
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
\[\begin{align*}A &= A_{Trapez} - \int_{0}^{2} f(x) dx \\[0.8em] &= \frac{\frac{2}{e} + \frac{1}{e}}{2} \cdot 2 - \int_{0}^{2} \frac{1}{2}xe^{1 - x} dx \\[0.8em] &= \frac{3}{e} - \left[ -\frac{1}{2}e^{1 - x}(x + 1) \right]_{0}^{2} \\[0.8em] &= \frac{3}{e} - \left[ -\frac{1}{2}e^{1 - 2}(2 + 1) - \left( -\frac{1}{2}e^{1 - 0}(0 + 1) \right) \right] \\[0.8em] &= \frac{3}{e} + \frac{3}{2e} - \frac{e}{2} \\[0.8em] &= \frac{6}{2e} + \frac{3}{2e} - \frac{e}{2} \\[0.8em] &= \frac{9}{2e} - \frac{e}{2} \\[0.8em] &\approx 0{,}30 \end{align*}\]
Der Flächeninhalt \(A\) des Flächenstücks, das der Graph \(G_{f}\) und die Wendetangente \(w\) im ersten Quadranten einschließen beträgt ca 0,30 FE (Flächeneinheiten).
2. Möglichkeit: Differenzfunktion integrieren
\(w(x) = -\frac{1}{2e}x + \frac{2}{e}\) (vgl. Teilaufgabe c, Gleichung der Wendetangente \(w\))
\(f(x) = \frac{1}{2}xe^{1 - x}\)
Aus der in Teilaufgabe d angefertigten Skizze geht hervor, dass die Wendetangente \(w\) im Intervall \([0;2]\) stets oberhalb des Graphen \(G_{f}\) verläuft.
Der Flächeninhalt \(A\) kann durch Integration der Differenzfunktion \(w(x) - f(x)\) bestimmt werden (vgl. Abiturskript - 1.6.4 Flächenberechnung, Flächeninhalt zwischen zwei Funktionsgraphen ).
\[A = \int_{0}^{2} (w(x) - f(x))dx\]
Da aus Teilaufgabe e bereits die Stammfunktion \(F(x) = -\frac{1}{2}e^{1 - x}(x + 1)\) von \(f\) bekannt ist, empfiehlt es sich, die Summenregel anzuwenden.
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
\[A = \int_{0}^{2} (w(x) - f(x))dx = \int_{0}^{2} w(x) dx - \int_{0}^{2} f(x) dx\]
Mithilfe des unbestimmten Integrals \(\displaystyle \int x^r \,dx = \frac{x^{r + 1}}{r + 1} + C \quad (r \neq -1)\) wird eine Stammfunktion \(W\) der Funktion \(w\) ermittelt.
\[\begin{align*}\int \left(-\frac{1}{2e}x + \frac{2}{e}\right)dx &= -\frac{1}{2e} \cdot \frac{1}{2}x^{2} + \frac{2}{e}x + C \\[0.8em] &= -\frac{1}{4e}x^{2} + \frac{2}{e}x + C \end{align*}\]
Mit \(C = 0\) ist die Funktion \(W \colon x \mapsto -\frac{1}{4e}x^{2} + \frac{2}{e}x\) eine Stammfunktion der Funktion \(w \colon x \mapsto -\frac{1}{2e}x + \frac{2}{e}\).
Damit lässt sich der Flächeninhalt \(A\) wie folgt berechnen:
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
\[\begin{align*}A &= \int_{0}^{2} (w(x) - f(x))dx \\[0.8em] &= \int_{0}^{2} w(x) dx - \int_{0}^{2} f(x) dx \\[0.8em] &= \int_{0}^{2} \left( -\frac{1}{2e}x + \frac{2}{e} \right) dx - \int_{0}^{2} \frac{1}{2}e^{1 - x} dx \\[0.8em] &= \left[ -\frac{1}{4e}x^{2} + \frac{2}{e}x \right]_{0}^{2} - \left[ -\frac{1}{2}e^{1 - x}(x + 1) \right]_{0}^{2} \\[0.8em] &= -\frac{1}{4e} \cdot 2^{2} + \frac{2}{e} \cdot 2 - \left( -\frac{1}{4e} \cdot 0^{2} + \frac{2}{e} \cdot 0 \right) - \left[ -\frac{1}{2}e^{1 - 2}(2 + 1) - \left( -\frac{1}{2}e^{1 - 0}(0 + 1) \right) \right] \\[0.8em] &= -\frac{1}{e} + \frac{4}{e} + \frac{3}{2e} - \frac{e}{2} \\[0.8em] &= \frac{3}{e} + \frac{3}{2e} - \frac{e}{2} \\[0.8em] &= \frac{6}{2e} + \frac{3}{2e} - \frac{e}{2} \\[0.8em] &= \frac{9}{2e} - \frac{e}{2} \\[0.8em] &\approx 0{,}30 \end{align*}\]
Der Flächeninhalt \(A\) des Flächenstücks, das der Graph \(G_{f}\) und die Wendetangente \(w\) im ersten Quadranten einschließen beträgt ca 0,30 FE (Flächeneinheiten).
g) Berechnung des Integrals \(\displaystyle \int_{0}^{+\infty} f(x) dx\) und geometrische Bedeutung des Ergebnisses
Für die Berechnung des uneigentlichen Integrals \(\displaystyle \int_{0}^{+\infty} f(x) dx\) wird dieses zunächst mithilfe der variablen oberen Integragtionsgrenze \(z\) integralfrei beschrieben und anschließend die Grenzwertbetrachtung für \(z \to +\infty\) durchgeführt (vgl. Abiturskript - 1.6.5 Uneigentliches Integrall).
\[\int_{0}^{+\infty} f(x) dx = \lim \limits_{z\, \to\, +\infty} \int_{0}^{z} f(x) dx\]
Integralfreie Darstellung des Integrals \(\displaystyle \int_{0}^{z} f(x) dx\):
Für die integralfreie Darstellung des Integrals \(\displaystyle \int_{0}^{z} f(x) dx\) (Integralfunktion) wird die Stammfunktion \(F\) aus Teilaufgabe e verwendet.
\(F(x) = -\frac{1}{2}e^{1 - x}(x + 1)\)
Integralfreie Darstellung einer Integralfunktion
Es gilt:
\(\displaystyle I_{a}(x) = \int_{a}^{x} f(t)\, dt = F(x) - F(a)\), wobei \(F\) eine Stammfunktion von \(f\) ist.
\[\begin{align*}\int_{0}^{z} f(x) dx &= \int_{0}^{z} \frac{1}{2}x \cdot e^{1 - x} dx \\[0.8em] &= \left[ -\frac{1}{2}e^{1 - x}(x + 1) \right]_{0}^{z} \\[0.8em] &= -\frac{1}{2}e^{1 - z}(z + 1) - \left[ -\frac{1}{2}e^{1 - 0}(0 + 1) \right] \\[0.8em] &= -\frac{1}{2}e^{1 - z}(z + 1) + \frac{e}{2} \end{align*}\]
Grenzwertbetrachtung für \(z \to +\infty\) durchführen (vgl. Abiturskript - 1.4 Grenzwerte):
Wichtiger Grenzwert
\[\lim \limits_{x \, \to \, +\infty} \frac{x^r}{e^x} = 0 \enspace (r > 0)\]
Für \(\,x \to +\infty\,\) wächst \(e^x\) „schneller" als jede Potenz \(x^r \enspace (r > 0)\).
(vgl. Merkhilfe)
\[\begin{align*}\lim \limits_{z\,\to\,+\infty} \left(-\frac{1}{2}e^{1 - z}(z + 1) + \frac{e}{2} \right) &= \lim \limits_{z\,\to\,+\infty} -\frac{1}{2}e^{1 - z}(z + 1) + \lim \limits_{z\,\to\,+\infty} \frac{e}{2} \\[0.8em] &= \lim \limits_{z\,\to\,+\infty} -\frac{1}{2}e^{1 - z}(z + 1) + \frac{e}{2} \\[0.8em] &= \lim \limits_{z\,\to\,+\infty} -\frac{1}{2}e^{-(z - 1)}(z + 1) + \frac{e}{2} & &| \; a^{-n} = \frac{1}{a^{n}} \\[0.8em] &= \lim \limits_{z\,\to\,+\infty} \underbrace{-\frac{z + 1}{2e^{z - 1}}}_{\to\,0} + \frac{e}{2} \\[0.8em] &= \frac{e}{2} \end{align*}\]
Für \(z \to +\infty\) wächst der Exponentialterm \(2e^{z - 1}\) „schneller" als der lineare Term \(z + 1\).
Geometrische Bedeutung des Ergebnisses \(\displaystyle \int_{0}^{+\infty} f(x) dx = \frac{e}{2}\):
Der Flächeninhalt des Flächenstücks, das der Graph \(G_{f}\) im Intervall \([0;+\infty[\) mit der \(x\)-Achse einschließt, ist mit \(\frac{e}{2}\) FE (Flächeneinheiten) endlich.


