Untersuchen Sie, ob die Punkte \(A(3|1|0)\), \(B(2|-1|-2)\), \(C(-2|1|-2)\) und \(D(4|3|-4)\) in einer Ebene liegen.
Drei Punkte, die nicht auf einer Geraden liegen, legen eine Ebene \(E\) fest.
Beispielsweise wählt man die Punkte \(A\), \(B\) und \(C\) und überprüft zunächst die lineare Unabhängigkeit der Verbindungsvektoren \(\overrightarrow{AB}\) und \(\overrightarrow{AC}\). Im Falle der linearen Unabhängigkeit spannen die Vektoren eine Ebene auf.
Eine Punktprobe untersucht, ob der vierte Punkt \(D\) ebenfalls in der Ebene liegt.
Die Gleichung der Ebene \(E\) kann in der Parameterform oder in der Normalenform aufgestellt werden.
Verbindungsvektoren \(\overrightarrow{AB}\) und \(\overrightarrow{AC}\) berechnen:
\(A(3|1|0)\), \(B(2|-1|-2)\), \(C(-2|1|-2)\)
\[\overrightarrow{AB} = \overrightarrow{B} - \overrightarrow{A} = \begin{pmatrix} 2 \\ -1 \\ -2 \end{pmatrix} - \begin{pmatrix} 3 \\ 1 \\ 0 \end{pmatrix} = \begin{pmatrix} -1 \\ -2 \\ -2 \end{pmatrix}\]
\[\overrightarrow{AC} = \overrightarrow{C} - \overrightarrow{A} = \begin{pmatrix} -2 \\ 1 \\ -2 \end{pmatrix} - \begin{pmatrix} 3 \\ 1 \\ 0 \end{pmatrix} = \begin{pmatrix} -5 \\ 0 \\ -2 \end{pmatrix}\]
Lineare Unabhängigkeit der Vektoren \(\overrightarrow{AB}\) und \(\overrightarrow{AC}\) überprüfen:
Die Vektoren \(\overrightarrow{AB}\) und \(\overrightarrow{AC}\) sind linear unabhängig, wenn \(\overrightarrow{AB} \neq k \cdot \overrightarrow{AC}; \; k \in \mathbb R\) gilt (vgl. Abiturskript - 2.1.2 Lineare (Un-)Abhängigkeit von Vektorenktoren).
\[\begin{align*} \overrightarrow{AB} &= k \cdot \overrightarrow{AC}; \; k \in \mathbb R \\[0.8em] \begin{pmatrix} -2 \\ -1 \\ -2 \end{pmatrix} &= k \cdot \begin{pmatrix} -5 \\ 0 \\ -2 \end{pmatrix}; \; k \in \mathbb R \end{align*}\]
\[\Longrightarrow \quad \left\{ \begin{align*} -1 &= -5k \quad \Longleftrightarrow \quad k = \textstyle \frac{1}{5} \\[0.8em] - 2 &= 0 \\[0.8em] -2 &= -2k \quad \Longleftrightarrow \quad k = 1 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Widerspruch!}\]
\[\Longrightarrow \quad \overrightarrow{AB} \neq k \cdot \overrightarrow{AC}; \; k \in \mathbb R\]
Also sind die Vektoren \(\overrightarrow{AB}\) und \(\overrightarrow{AC}\) linear unabhängig und spannen eine Ebene auf.
1. Möglichkeit: Ebenengleichung in Parameterform aufstellen
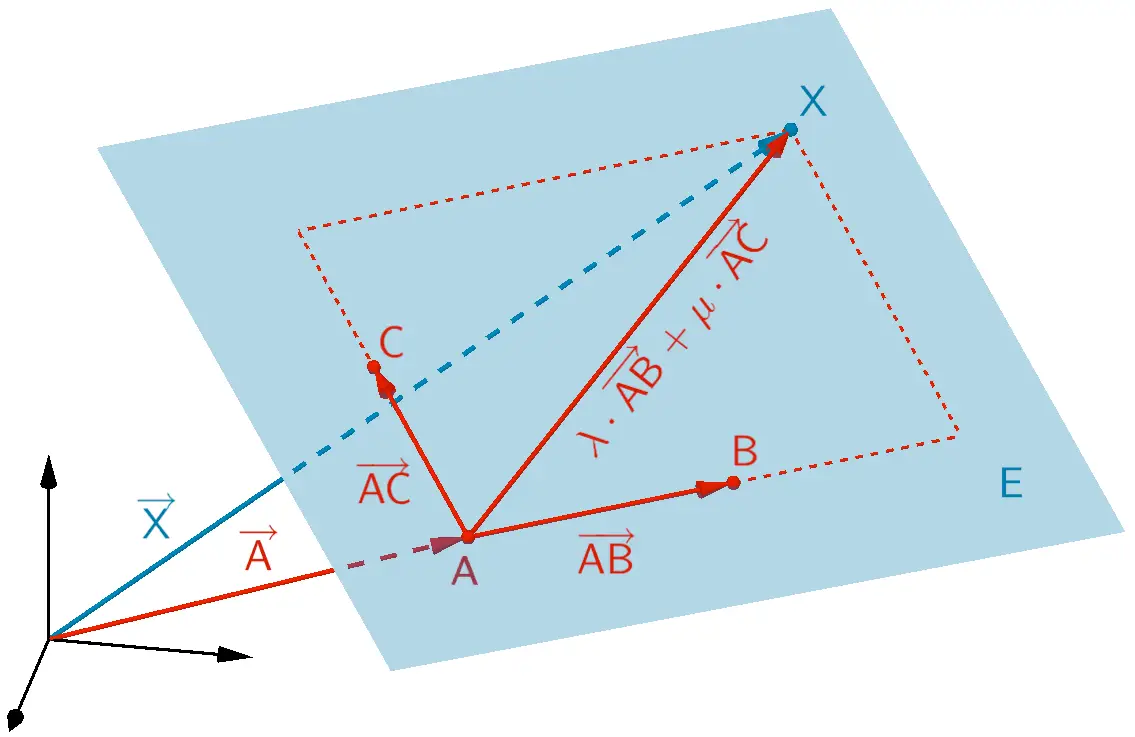
Veranschaulichung: Ebenengleichung einer Ebene \(E\) durch drei Punkte \(A\), \(B\) und \(C\) in Parameterform (vgl. Abiturskript - 2.2.2 Ebenengleichung in Parameterform)
Es sei \(A(3|1|0)\) der Aufpunkt der Gleichung der Ebene \(E\) in Parameterform.
\(\overrightarrow{AB} = \begin{pmatrix} -1 \\ -2 \\ -2 \end{pmatrix}; \; \overrightarrow{AC} = \begin{pmatrix} -5 \\ 0 \\ -2 \end{pmatrix}\)
\[E \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{AB} + \mu \cdot \overrightarrow{AC}; \; \lambda, \mu \in \mathbb R\]
\[E \colon \overrightarrow{X} = \begin{pmatrix} 3 \\ 1 \\ 0 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -1 \\ -2 \\ -2 \end{pmatrix} + \mu \cdot \begin{pmatrix} -5 \\ 0 \\ -2 \end{pmatrix}; \lambda, \mu \in \mathbb R\]
Prüfen, ob der Punkt \(D(4|3|-4)\) in der Ebene \(E\) liegt (Punktprobe):
Hierfür wird der Ortsvektor \(\overrightarrow{D}\) und der Ortsvektor \(\overrightarrow{X}\) der Gleichung der Ebene \(E\) gleichgesetzt. Zeilenweise gelesen ergibt die Vektorgleichung ein (überbestimmtes) lineares Gleichungssystem.
\[\begin{pmatrix} 4 \\ 3 \\ -4 \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \\ 0 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -1 \\ -2 \\ -2 \end{pmatrix} + \mu \cdot \begin{pmatrix} -5 \\ 0 \\ -2 \end{pmatrix}\]
\[\begin{align*} \text{I} & & & \quad \; 4 = 3 - \enspace \lambda - 5\mu \\[0.8em] \text{II} & & \wedge \enspace & \quad \; 3 = 1 - 2\lambda \quad \Longleftrightarrow \quad \lambda = -1 \\[0.8em] \text{III} & &\wedge \enspace & -4 = \enspace \; -\,2\lambda - 2\mu \end{align*}\]
\[\begin{align*} \lambda = -1 \; \text{in I}\colon \; 4 &= 3 - (-1) - 5\mu \\[0.8em] 4 &= 4 - 5\mu &&| - 4 \\[0.8em] 0 &= -5\mu \\[0.8em] 0 &= \mu \end{align*}\]
\[\begin{align*}\lambda = -1, \mu = 0 \; \text{in III} \colon \; -4 &= -2 \colon (-1) - 2 \cdot 0 \\[0.8em] -4 &= 2 \qquad (\text{f}) \end{align*}\]
Das Gleichungssystem besitzt keine eindeutige Lösung. Der Punkt \(D\) liegt folglich nicht in der Ebene \(E\).
Schlussfolgerung:
Die Punkte \(A\), \(B\), \(C\) und \(D\) liegen nicht in einer Ebene.
2. Möglichkeit: Ebenengleichung in Normalenform aufstellen
Das Vektorprodukt der linear unabhängigen Vektoren \(\overrightarrow{AB}\) und \(\overrightarrow{AC}\) (vgl. oben) liefert einen Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\), welche die Punkte \(A\), \(B\) und \(C\) festlegen (vgl. Abiturskript - 2.2.3 Ebenengleichung in Normalenform ).
Vektorprodukt (Kreuzprodukt)
Das Vektorprodukt \(\overrightarrow{a} \times \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) erzeugt einen neuen Vektor \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) mit den Eigenschaften:
\(\overrightarrow{c}\) ist sowohl zu \(\overrightarrow{a}\) als auch zu \(\overrightarrow{b}\) senkrecht.
\[\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b} \quad \Longrightarrow \quad \overrightarrow{c} \perp \overrightarrow{a}, \enspace \overrightarrow{c} \perp \overrightarrow{b}\]
Der Betrag des Vektorprodukts zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) ist gleich dem Produkt aus den Beträgen der Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) und dem Sinus des von ihnen eingeschlossenen Winkels \(\varphi\).
\[\vert \overrightarrow{a} \times \overrightarrow{b} \vert = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \sin{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Die Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) bilden in dieser Reihenfolge ein Rechtssystem. Rechtehandregel: Weist \(\overrightarrow{a}\) in Richtung des Daumens und \(\overrightarrow{b}\) in Richtung des Zeigefingers, dann weist \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) in Richtung des Mittelfingers.
Berechnung eines Vektorprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \times \overrightarrow{b} = \begin {pmatrix} a_1 \\ a_2 \\ a_3 \end {pmatrix} \times \begin {pmatrix} b_1 \\ b_2 \\ b_3 \end {pmatrix} = \begin {pmatrix} a_2 \cdot b_3 - a_3 \cdot b_2 \\ a_3 \cdot b_1 - a_1 \cdot b_3 \\ a_1 \cdot b_2 - a_2 \cdot b_1 \end {pmatrix}\]
\(\overrightarrow{AB} = \begin{pmatrix} -1 \\ -2 \\ -2 \end{pmatrix}; \; \overrightarrow{AC} = \begin{pmatrix} -5 \\ 0 \\ -2 \end{pmatrix}\) (vgl. oben)
\[\begin{align*} \overrightarrow{AB} \times \overrightarrow{AC} &= \begin{pmatrix} -1 \\ -2 \\ -2 \end{pmatrix} \times \begin{pmatrix} -5 \\ 0 \\ -2 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} (-2)& \cdot & (-2) & - & (-2) & \cdot & 0 \\ (-2) & \cdot & (-5) & - & (-1) & \cdot & (-2) \\ (-1) & \cdot & 0 & - & (-2) & \cdot & (-5) \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 4 \\ 8 \\ -10 \end{pmatrix} \\[0.8em] &= 2 \cdot \begin{pmatrix} 2 \\ 4 \\ -5 \end{pmatrix}\end{align*}\]
\[\Longrightarrow \quad \overrightarrow{n}_{E} = \begin{pmatrix} 2 \\ 4 \\ -5 \end{pmatrix}\]
Es sei \(A(3|1|0)\) der Aufpunkt der Gleichung der Ebene \(E\) in Normalenform.
Ebenengleichung in Normalenform (vgl. Merkhilfe)
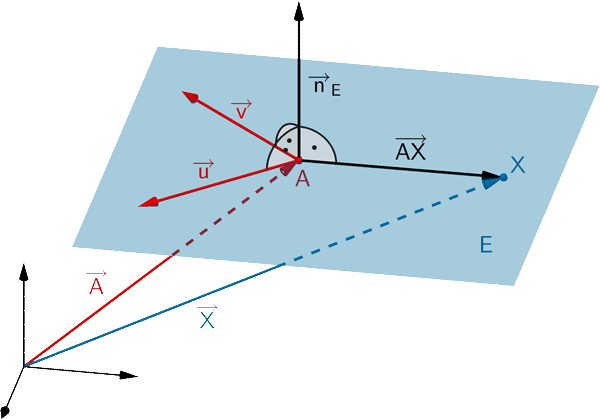
Jeden Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]
Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]
\[E \colon \begin{pmatrix} 2 \\ 4 \\ -5 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} 3 \\ 1 \\ 0 \end{pmatrix} \right] = 0\]
Prüfen, ob der Punkt \(D(4|3|-4)\) in der Ebene \(E\) liegt (Punktprobe):
Hierfür wird der Ortsvektor \(\overrightarrow{D}\) anstelle des Ortsvektors \(\overrightarrow{X}\) der Gleichung der Ebene \(E\) in Normalenform (in Vektordarstellung) gesetzt und das Skalarprodukt ausmultipliziert.
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin{align*}D \in E \colon \begin{pmatrix} 2 \\ 4 \\ -5 \end{pmatrix} \circ \left[ \begin{pmatrix} 4 \\ 3 \\ -4 \end{pmatrix} - \begin{pmatrix} 3 \\ 1 \\ 0 \end{pmatrix} \right] &= 0 \\[0.8em] \begin{pmatrix} 2 \\ 4 \\ -5 \end{pmatrix} \circ \begin{pmatrix} 1 \\ 2 \\ -4 \end{pmatrix} &= 0 \\[0.8em] 2 \cdot 1 + 4 \cdot 2 + (-5) \cdot (-4) &= 0 \\[0.8em] 30 &= 0 \qquad (\text{f}) \end{align*}\]
Die Gleichung liefert eine falsche Aussage. Folglich liegt der Punkt \(D\) nicht in der Ebene \(E\).
Schlussfolgerung:
Die Punkte \(A\), \(B\), \(C\) und \(D\) liegen nicht in einer Ebene.

