Teilaufgabe 2
Lösung zu Teilaufgabe 2
Nachweis der Stammfunktion \(F(x)\)
\[F(x) = \frac{1}{4}x^2 \cdot (2\ln x - 1); \qquad D = \mathbb R^+\]
\[f(x) = x \cdot \ln x\]
Zu beweisen: \(F'(x) = f(x) \quad \Longleftrightarrow \quad \left ( \frac{1}{4}x^2 \cdot (2\ln x - 1) \right )' = x \cdot \ln x\)
\[\begin{align*} F'(x) &= 2 \cdot \frac{1}{4}x \cdot (2\ln x - 1) + \frac{1}{4}x^2 \cdot \frac{2}{x} \\[0.8em] &= x \cdot \ln x - \frac{1}{2}x + \frac{1}{2}x \\[0.8em] &= x \cdot \ln x \\[0.8em] F'(x) &= f(x) \end{align*}\]
\(\Longrightarrow \quad F(x)\) ist Stammfunktion von \(f(x)\).
Stammfunktion von \(f\), die in \(x = 1\) eine Nullstelle hat
Die Menge aller Stammfunktionen von \(f\) ist gegeben durch das unbestimmte Integral:
\[\int f(x)\,dx = F(x) + C; \qquad C \in \mathbb R\]
Die gesuchte Stammfunktion \(F_C(x)\), die in \(x = 1\) eine Nullstelle hat, unterscheidet sich von \(F(x)\) nur um eine additive Integrationskonstnate \(C\).
\[F_C(x) = F(x) + C \quad \Longleftrightarrow \quad F_C(x) = \frac{1}{4}x^2 \cdot (2\ln x - 1) + C\]
Die Bedingung, dass die Stamfunktion \(F_C(x)\) in \(x = 1\) ein Nullstelle haben soll, legt die Integrationskonstante \(C\) fest:
\[\begin {align*}F_C(1) \overset{!}{=} 0 \quad \Longrightarrow \quad \frac{1}{4} \cdot 1^2 \cdot (2 \underbrace{\ln 1}_{0} - 1) + C &= 0 \\[0.8em] -\frac{1}{4} + C &= 0 \\[0.8em] C &= \frac{1}{4} \end {align*}\]
\[\Longrightarrow \quad F_{\frac{1}{4}}(x) = \frac{1}{4}x^2 \cdot (2\ln x - 1) + \frac{1}{4}\]
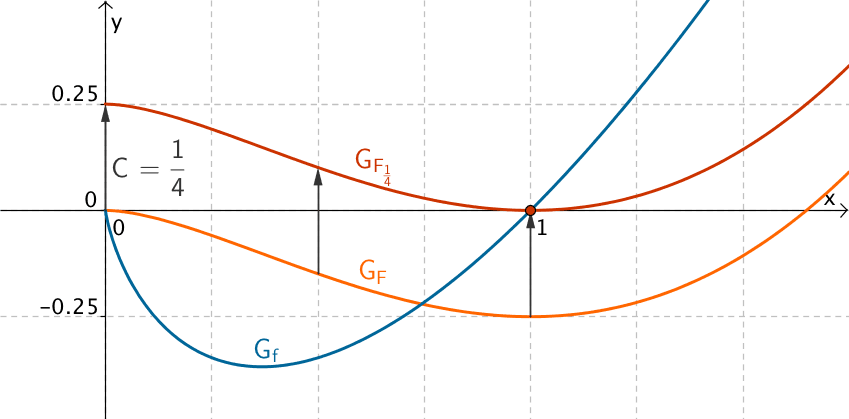
Der Graph von \(F_{\frac{1}{4}}\) geht aus dem Graphen von \(F\) durch Verschiebung in \(y\)-Richtung um \(C = \frac{1}{4}\) hervor.
