Mathematik Abitur Bayern 2011 G8 Analysis II Teil 2 - Aufgaben mit Lösungen

Gegeben ist die in \(\mathbb R\) definierte Funktion \(f : x \mapsto 6 \cdot e^{-0{,}5x} + x\). Der Graph von \(f\) wird mit \(G_f\) bezeichnet.

Untersuchen Sie das Monotonie- und das Krümmungsverhalten von \(G_f\). Bestimmen Sie Lage und Art des Extrempunkts \(E(x_E|y_E)\) von \(G_f\).

(zur Kontrolle: \(x_E = 2 \cdot \ln 3; \enspace f''(x) = 1{,}5 \cdot e^{-0{,}5x}\))

(10 BE)

Geben Sie das Verhalten von \(f\) für \(x \to -\infty\) an. Machen Sie plausibel, dass \(G_f\) für \(x \to +\infty\) die Gerade mit der Gleichung \(y = x\) als schräge Asymptote besitzt.

(3 BE)

Bestimmen Sie die Gleichung der Tangente an \(G_f\) im Punkt \((0|6)\). Skizzieren Sie \(G_f\) unter Verwendung der bisherigen Ergebnisse in ein geeignet anzulegendes Koordinatensystem.

(6 BE)

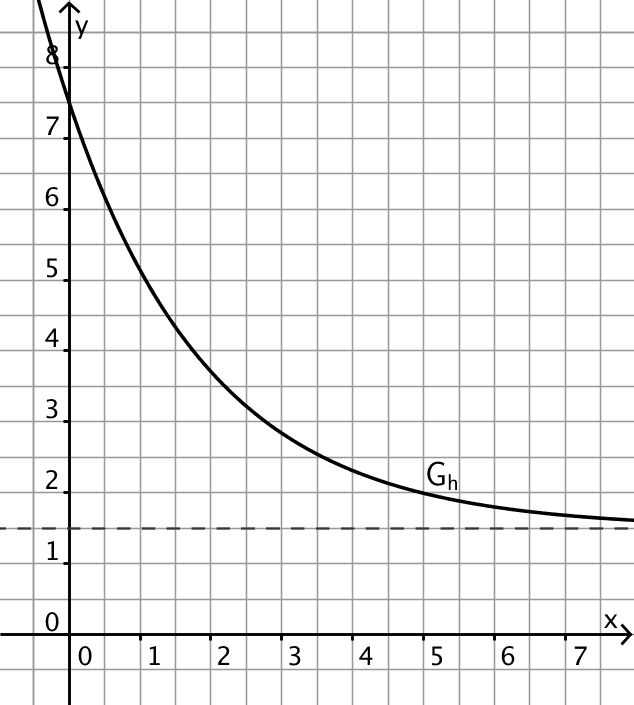
Gegeben ist die in \(\mathbb R\) definierte Funktion \(h : x \mapsto 6 \cdot e^{-0{,}5x} + 1{,}5\). Die Abbildung zeigt den in \(\mathbb R\) streng monoton fallenden Graphen \(G_h\) von \(h\) sowie dessen Asymptote, die durch die Gleichung \(y = 1{,}5\) gegeben ist.

Beschreiben Sie, wie \(G_h\) aus dem Graphen der in \(\mathbb R\) definierten natürlichen Exponentialfunktion \(x \mapsto e^x\) hervorgeht.

(4 BE)

Für \(x \geq 0\) beschreibt die Funktion \(h\) modelhaft die zeitliche Entwicklung des momentanen Schadstoffausstoßes einer Maschine. Dabei ist \(x\) die seit dem Start der Maschine vergangene Zeit in Minuten und \(h(x)\) die momentane Schadstoffausstoßrate in Milligramm pro Minute.

Geben Sie in diesem Sachzusammenhang die Bedeutung des Monotonieverhaltens von \(G_h\) sowie des Grenzwerts von \(h\) für \(x \to +\infty\) an.

(3 BE)

Bestimmen Sie den Inhalt des Flächenstücks, das \(G_h\), die Koordinatenachsen und die Gerade mit der Gleichung \(x = 5\) einschließen. Interpretieren Sie das Ergebnis im Sachzusammenhang.

(6 BE)

Gegeben ist die Schar der Funktionen \(f_a : x \mapsto 6 \cdot e^{-0{,}5x} - a \cdot x\) mit \(a \in \mathbb R^+\) und Definitionsmenge \(\mathbb R\).

Weisen Sie nach, dass die Graphen aller Funktionen der Schar die \(y\)-Achse im selben Punkt schneiden und in \(\mathbb R\) streng monoton fallend sind. Zeigen Sie, dass \(\lim \limits_{x \, \to \, +\infty} f_a(x) = -\infty\) gilt.

(5 BE)

Aus den Ergebnissen der Aufgabe 3a ergibt sich, dass jede Funktion der Schar genau eine Nullstelle besitzt. Bestimmen Sie für diese Nullstelle in Abhängigkeit von \(a\) einen Näherungswert \(x_1\), indem Sie den ersten Schritt des Newton-Verfahrens mit dem Startwert \(x_0 = 0\) durchführen.

(3 BE)