Weisen Sie nach, dass der Koordinatenursprung \(O\) mit den Punkten \(A\), \(B\) und \(C\) ein Rechteck \(OABC\) festlegt. Bestätigen Sie, dass dieses Rechteck den Flächeninhalt 6000 besitzt, und zeichnen Sie es in ein Koordinatensystem (vgl. Abbildung) ein.
(6 BE)
Lösung zu Teilaufgabe b
Nachweis, dass das Viereck \(OABC\) ein Rechteck ist
Der Koordinatenursprung \(O\) legt mit den Punkten \(A\), \(B\) und \(C\) ein Rechteck fest, wenn je zwei gegenüberliegende Seiten des Vierecks \(OABC\) gleiche Länge besitzen und zwei anliegende Seiten senkrecht aufeinander stehen (Orthogonalität).
\[\overline{OA} = \overline{CB} \quad \Longleftrightarrow \quad \left| \overrightarrow{OA} \right| = \left| \overrightarrow{CB} \right|\]
\[\overline{OC} = \overline{AB} \quad \Longleftrightarrow \quad \left| \overrightarrow{OC} \right| = \left| \overrightarrow{AB} \right|\]
z.B. \(\;\overrightarrow{OA} \perp \overrightarrow{OC}\)
Überprüfen der Seitenlängen:
\[\overrightarrow{OA} = \overrightarrow A = \begin {pmatrix} 0 \\ 60 \\ 0 \end {pmatrix}\]
\[\overrightarrow{CB} = \overrightarrow B - \overrightarrow C = \begin {pmatrix} -80 \\ 60 \\ 60 \end {pmatrix} - \begin {pmatrix} -80 \\ 0 \\ 60 \end {pmatrix} = \begin {pmatrix} 0 \\ 60 \\ 0 \end {pmatrix}\]
\[\Longrightarrow \quad \overrightarrow{OA} = \overrightarrow{CB} \quad \Longrightarrow \quad \overline{OA} = \overline{CB}\]
\[\overrightarrow{OC} = \overrightarrow C = \begin {pmatrix} -80 \\ 0 \\ 60 \end {pmatrix}\]
\[\overrightarrow{AB} = \overrightarrow B - \overrightarrow A = \begin {pmatrix} -80 \\ 60 \\ 60 \end {pmatrix} - \begin {pmatrix} 0 \\ 60 \\ 0 \end {pmatrix} = \begin {pmatrix} -80 \\ 0 \\ 60 \end {pmatrix}\]
\[\Longrightarrow \quad \overrightarrow{OC} = \overrightarrow{AB} \quad \Longrightarrow \quad \overline{OC} = \overline{AB}\]
Überprüfen der Orthogonalität:
Anwendung des Skalarprodukts:
Orthogonale (zueinander senkrechte) Vektoren (vgl. Merkhilfe)
\[\overrightarrow{a} \perp \overrightarrow{b} \quad \Longleftrightarrow \quad \overrightarrow{a} \circ \overrightarrow{b} \quad (\overrightarrow{a} \neq \overrightarrow{0},\; \overrightarrow{b} \neq \overrightarrow{0})\]
\[\overrightarrow{OA} \circ \overrightarrow{OC} \overset{!}{=} 0\]
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin {align*} \overrightarrow{OA} \circ \overrightarrow{OC} &= \overrightarrow A \circ \overrightarrow C \\[0.8em] &= \begin {pmatrix} 0 \\ 60 \\ 0 \end {pmatrix} \circ \begin {pmatrix} -80 \\ 0 \\ 60 \end {pmatrix} \\[0.8em] &= 0 \cdot (-80) + 60 \cdot 0 + 0 \cdot 60 \\[0.8em] &= 0 \end{align*}\]
\[\Longrightarrow \quad \overrightarrow{OA} \perp \overrightarrow{OC}\]
\(\Longrightarrow \quad\) Der Koordinatenursprung \(O\) legt mit den Punkten \(A\), \(B\) und \(C\) ein Rechteck fest.
Flächeninhalt des Rechtecks \(OABC\)
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[ \begin {align*} A_{OABC} &= \left| \overrightarrow{OA} \right| \cdot \left| \overrightarrow{OC} \right| \\[0.8em] &= \left| \overrightarrow A \right| \cdot \left| \overrightarrow C \right| \\[0.8em] &= \left| \begin {pmatrix} 0 \\ 60 \\ 0 \end {pmatrix} \right| \cdot \left| \begin {pmatrix} -80 \\ 0 \\ 60 \end {pmatrix} \right| \\[0.8em] &= \sqrt{0^2 + 60^2 + 0^2} \cdot \sqrt{(-80)^2 + 0^2 + 60^2} \\[0.8em] &= 60 \cdot 100 \\[0.8em] &= 6000 \end {align*} \]
Alternativer Lösungsansatz: Anwenden des Vektorprodukts
Anwendung des Vekorprodukts:
Flächeninhalt eines Parallelogramms
Flächeninhalt des von den Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) aufgespannten Parallelogramms:
\[A = \vert \; \overrightarrow{a} \times \overrightarrow{b} \; \vert = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \sin \varphi\]

Vektorprodukt (Kreuzprodukt)
Das Vektorprodukt \(\overrightarrow{a} \times \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) erzeugt einen neuen Vektor \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) mit den Eigenschaften:
\(\overrightarrow{c}\) ist sowohl zu \(\overrightarrow{a}\) als auch zu \(\overrightarrow{b}\) senkrecht.
\[\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b} \quad \Longrightarrow \quad \overrightarrow{c} \perp \overrightarrow{a}, \enspace \overrightarrow{c} \perp \overrightarrow{b}\]
Der Betrag des Vektorprodukts zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) ist gleich dem Produkt aus den Beträgen der Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) und dem Sinus des von ihnen eingeschlossenen Winkels \(\varphi\).
\[\vert \overrightarrow{a} \times \overrightarrow{b} \vert = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \sin{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Die Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) bilden in dieser Reihenfolge ein Rechtssystem. Rechtehandregel: Weist \(\overrightarrow{a}\) in Richtung des Daumens und \(\overrightarrow{b}\) in Richtung des Zeigefingers, dann weist \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) in Richtung des Mittelfingers.
Berechnung eines Vektorprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \times \overrightarrow{b} = \begin {pmatrix} a_1 \\ a_2 \\ a_3 \end {pmatrix} \times \begin {pmatrix} b_1 \\ b_2 \\ b_3 \end {pmatrix} = \begin {pmatrix} a_2 \cdot b_3 - a_3 \cdot b_2 \\ a_3 \cdot b_1 - a_1 \cdot b_3 \\ a_1 \cdot b_2 - a_2 \cdot b_1 \end {pmatrix}\]
\[ \begin {align*} A_{OABC} &= \left| \overrightarrow{OA} \times \overrightarrow{OC} \right| \\[0.8em] &= \left| \overrightarrow A \times \overrightarrow C \right| \\[0.8em] &= \left| \begin {pmatrix} 0 \\ 60 \\ 0 \end {pmatrix} \times \begin {pmatrix} -80 \\ 0 \\ 60 \end {pmatrix} \right| \\[0.8em] &= \left| \begin {pmatrix} 60 & \cdot & 60 & - & 0 & \cdot & 0 \\ 0 & \cdot & (-80) & - & 0 & \cdot & 60 \\ 0 & \cdot & 0 & - & 60 & \cdot & (-80) \end {pmatrix} \right| \\[0.8em] &= \left| \begin {pmatrix} 3600 \\ 0 \\ 4800 \end {pmatrix} \right| \\[0.8em] &= \sqrt{3600^2 + 0^2 + 4800^2} \\[0.8em] &= 6000 \end {align*} \]
Zeichnung des Rechtecks \(OABC\)
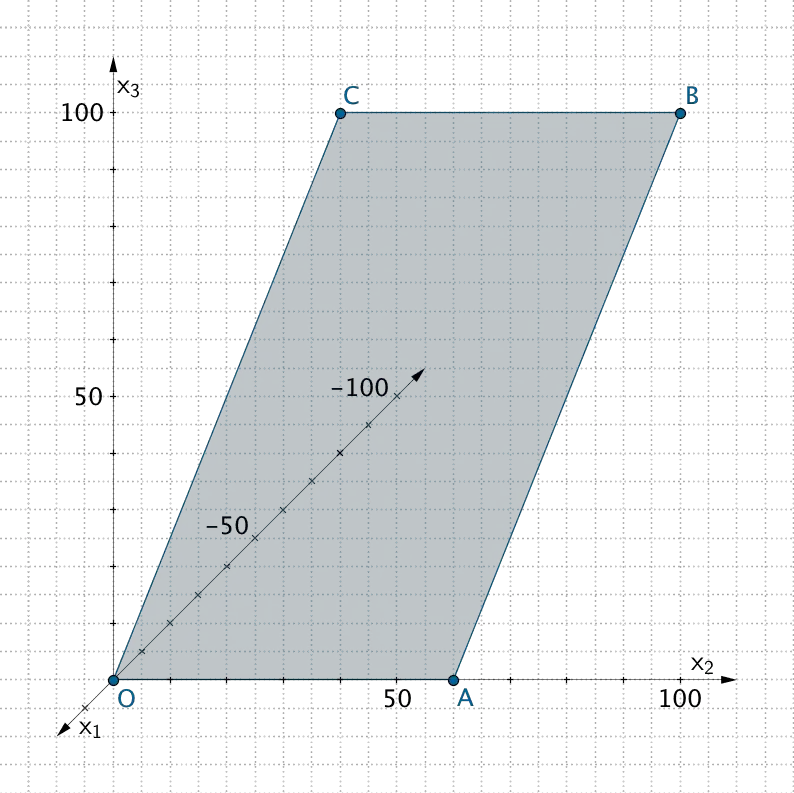
Lage des Rechtecks \(\,OABC\,\)

