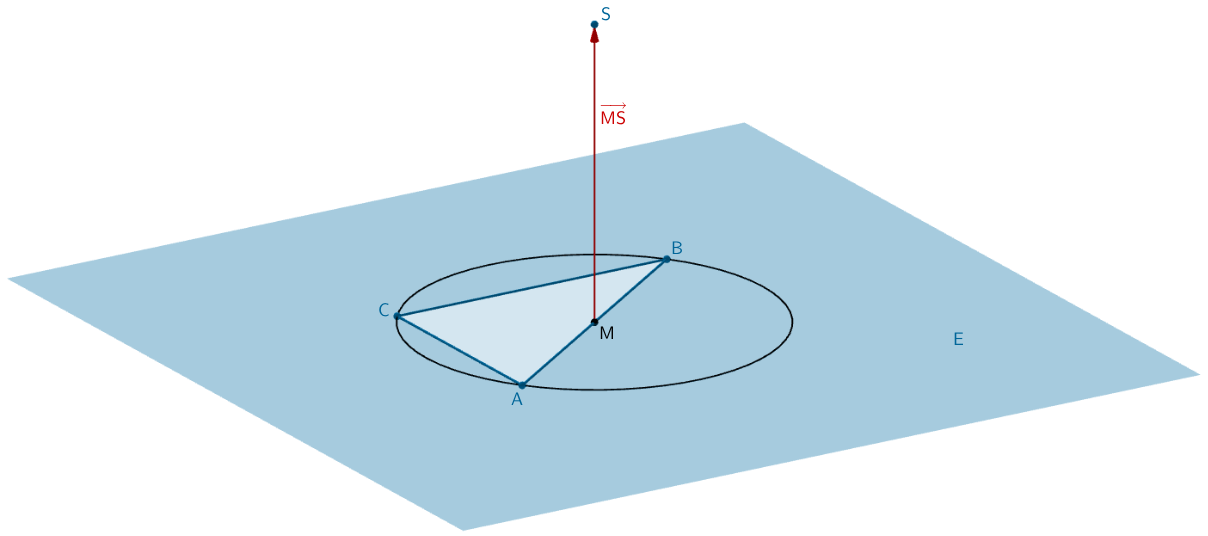
Der Umkreis des Dreiecks \(ABC\) und der Punkt \(S\) legen einen Kegel fest. Zeigen Sie, dass es sich um einen geraden Kegel handelt, der Mittelpunkt des Grundkreises also zugleich der Höhenfußpunkt des Kegels ist. Berechnen Sie, um wie viel Prozent das Volumen des Kegels größer ist als das Volumen der Pyramide \(ABCS\).
(7 BE)
Lösung zu Teilaufgabe f
Nachweis, dass der Mittelpunkt \(M\) zugleich Höhenfußpunkt des Kegels ist
Satz des Thales
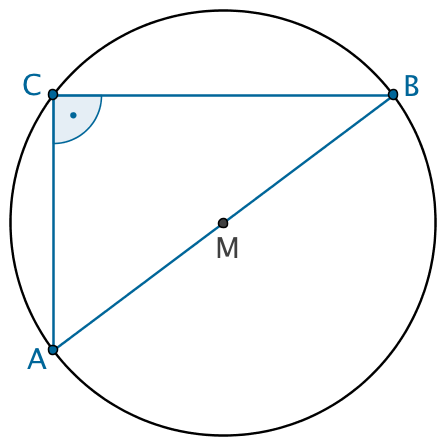
Liegt der Punkt \(C\) eines Dreiecks \(ABC\) auf einem Kreis mit dem Durchmesser \([AB]\), ist der Winkel bei Punkt \(C\) ein rechter Winkel.
Der Mittelpunkt des Umkreises eines rechtwinkligen Dreiecks liegt immer in der Mitte der Hypotenuse.
Der Umkreis eines rechtwinkligen Dreiecks ist der Thaleskreis. Folglich liegt der Mittelpunkt \(M\) des Umkreises des Dreiecks \(ABC\) auf der Mitte der Strecke \([AB]\) (Hypotenuse).
1. Lösungsansatz: Mittelpunkt \(M\) berechnen und \(\overrightarrow{MS} \perp E\) nachweisen
Der Mittelpunkt \(M\) des Umkreises des Dreiecks \(ABC\) ist Höhenfußpunkt des Kegels, wenn der Vektor \(\overrightarrow{MS}\) senkrecht auf der Ebene \(E\) steht.
Mittelpunkt \(M\) des Umkreises berechnen:
Mittelpunkt einer Strecke
Für den Ortsvektor \(\overrightarrow{M}\) des Mittelpunkts \(M\) einer Strecke \([AB]\) gilt:
\[\overrightarrow{M} = \frac{1}{2} \left( \overrightarrow{A} + \overrightarrow{B} \right)\]
\[\begin{align*} \overrightarrow M &= \frac{1}{2}\left( \overrightarrow A + \overrightarrow B \right) \\[0.8em] &= \frac{1}{2} \left[ \begin {pmatrix} 1 \\ 7 \\ 3 \end {pmatrix} + \begin {pmatrix} 6 \\ -7 \\ 1 \end {pmatrix} \right] \\[0.8em] &= \begin {pmatrix} 3{,}5 \\ 0 \\ 2 \end {pmatrix} \end{align*}\]
\[\Longrightarrow \quad M(3{,}5|0|2)\]
Nachweis, dass gilt: \(\overrightarrow{MS} \perp E\):
Der Vektor \(\overrightarrow{MS}\) steht senkrecht auf der Ebene \(E\), wenn er ein Vielfaches des Normalenvektors \(\overrightarrow{n}_E\) der Ebene \(E\) ist (Kollinearität, Lineare Abhängigkeit).
Lineare (Un-)Abhängigkeit von zwei Vektoren
Zwei Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) sind
linear abhängig, wenn
\(\overrightarrow{a} \parallel \overrightarrow{b}\quad\) bzw. \(\quad\overrightarrow{a} = k \cdot \overrightarrow{b}\,; \enspace k \in \mathbb R \quad\) gilt.
linear unabhängig, wenn
\(\overrightarrow{a} \nparallel \overrightarrow{b}\quad\) bzw. \(\quad\overrightarrow{a} \neq k \cdot \overrightarrow{b}\,; \enspace k \in \mathbb R \quad\) gilt.
Lineare (Un-)Abhängigkeit von drei Vektoren
Drei Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) sind
linear abhängig, wenn
sie in einer Ebene liegen bzw. wenn
die lineare Vektorgleichung \(\overrightarrow{c} = r \cdot \overrightarrow{a} + s \cdot \overrightarrow{b}\) eine eindeutige Lösung hat.
linear unabhängig, wenn
sie den Raum \(\mathbb R^{3}\) aufspannen bzw. wenn
die lineare Vektorgleichung \(\overrightarrow{c} = r \cdot \overrightarrow{a} + s \cdot \overrightarrow{b}\) keine Lösung hat.
Bei der Untersuchung der linearen (Un)Abhängigkeit dreier Vektoren spielt es keine Rolle, welche der drei Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) oder \(\overrightarrow{c}\) man als Linearkombination der beiden anderen Vektoren darzustellen versucht.
\(\overrightarrow{n}_E = \begin {pmatrix} 2 \\ 1 \\ -2 \end {pmatrix}\) (siehe Teilaufgabe c)
\[\overrightarrow{MS} = \overrightarrow S - \overrightarrow M = \begin {pmatrix} 11{,}5 \\ 4 \\ -6 \end {pmatrix} - \begin {pmatrix} 3{,}5 \\ 0 \\ 2 \end {pmatrix} = \begin {pmatrix} 8 \\ 4 \\ -8 \end {pmatrix} = 4 \cdot \begin {pmatrix} 2 \\ 1 \\ -2 \end {pmatrix}\]
\[\Longrightarrow \quad \overrightarrow{MS}= 4 \cdot \overrightarrow{n}_E\]
\[\Longrightarrow \quad \overrightarrow{MS} \perp E\]
\(\Longrightarrow \quad\) Der Kegel, den der Umkreis des Dreiecks \(ABC\) mit dem Punkt \(S\) festlegt, ist ein gerader Kegel.
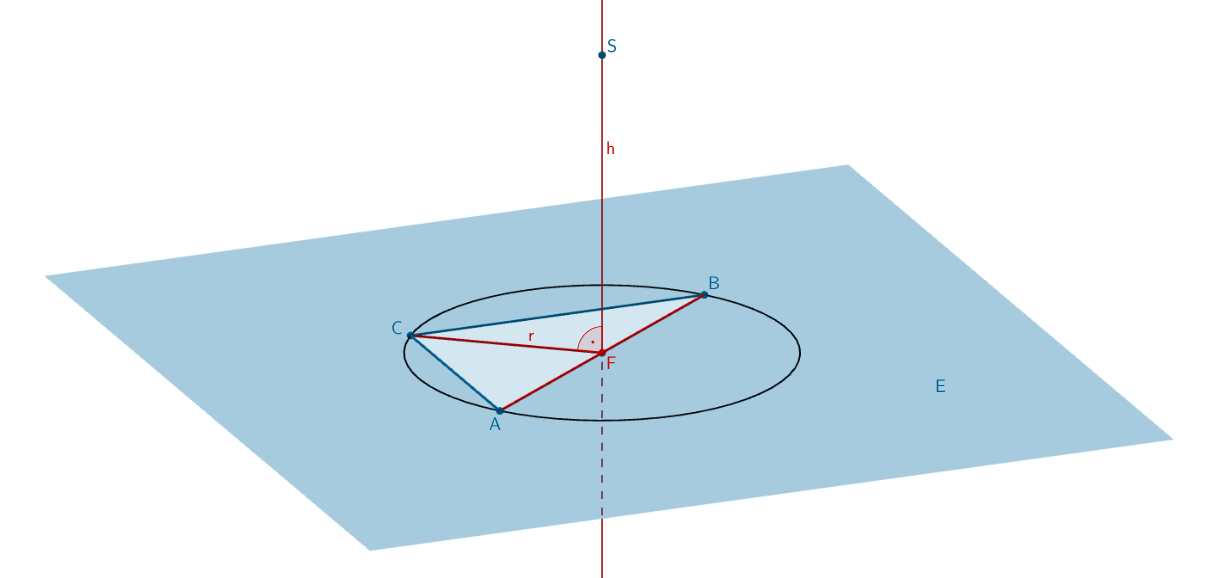
2. Lösungsansatz: Nachweisen, dass der Lotfußpunkt von \(S\) Mittelpunkt des Umkreises ist
Die Lotgerade \(h\) mit \(S \in h\) schneidet die Ebene \(E\) im Lotfußpunkt \(F\). Der Umkreis des Dreiecks \(ABC\) und der Punkt \(S\) legen dann einen geraden Kegel fest, wenn gilt: \(\overline{FA} = \overline{FB} = \overline{FC} = r\).
Lotgerade \(h\) bestimmen:
Lotgerade auf eine Ebene
\[E\,\colon \overrightarrow{n}_E \circ (\overrightarrow{X} - \overrightarrow{A}) = 0; \quad P\,(p_1|p_2|p_3)\]
Die Lotgerade \(\ell\) mit \(P \in \ell\) auf eine Ebene \(E\) ist durch den Ortsvektor \(\overrightarrow{P}\) und den Normalenvektor \(\overrightarrow{n}_E\) eindeutig bestimmt:
\[\ell\,\colon \overrightarrow{X} = \overrightarrow{P} + \lambda \cdot \overrightarrow{n}_E; \; \lambda \in \mathbb R\]
\[h \colon \enspace \overrightarrow X = \overrightarrow S + \mu \cdot \overrightarrow{v}_h\,; \quad \mu \in \mathbb R\]
Die Lotgerade \(h\) steht senkrecht auf der Ebene \(E\).
\(\Longrightarrow \quad \overrightarrow {v}_h = \overrightarrow {n}_E = \begin {pmatrix} 2 \\ 1 \\ -2 \end {pmatrix}\) (siehe Teilaufgabe c)
Mit \(S(11{,}5|4|-6)\) folgt:
\[h \colon \enspace \overrightarrow X = \begin {pmatrix} 11{,}5 \\ 4 \\ -6 \end {pmatrix} + \mu \cdot \begin {pmatrix} 2 \\ 1 \\ -2 \end {pmatrix}\]
Lotfußpunkt \(F\) berechnen:
Zur Berechnung des Lotfußpunktes \(F\) (Schnittpunkt \(h, E\)) setzt man die Koordinaten des Ortsvektors \(\overrightarrow X\) aus der Geradengleichung von \(h\) in die Normalengleichung der Ebene \(E\) ein und löst die Gleichung nach dem Parameter \(\mu\) auf.
\[h \colon \enspace \overrightarrow X = \begin {pmatrix} 11{,}5 \\ 4 \\ -6 \end {pmatrix} + \mu \cdot \begin {pmatrix} 2 \\ 1 \\ -2 \end {pmatrix}\]
\(E \colon \enspace 2x_1 + x_2 - 2x_3 - 3 = 0\) (siehe Teilaufgabe c )
\[ \begin {align*} h \cap E \colon \enspace 2 \cdot (11{,}5 + 2 \mu) + 4 + \mu - 2 \cdot (-6 - 2 \mu) - 3 &= 0 \\[0.8em] 23 + 4 \mu + 4 + \mu + 12 + 4 \mu - 3 &= 0 \\[0.8em] 9 \mu + 36 &= 0 \\[0.8em] 9 \mu &= -36 \\[0.8em] \mu &= -4 \end {align*} \]
Parameterwert \(\mu = -4\) in \(h\) einsetzen:
\[F \in h \colon \enspace \overrightarrow {F} = \begin {pmatrix} 11{,}5 \\ 4 \\ -6 \end {pmatrix} - 4 \cdot \begin {pmatrix} 2 \\ 1 \\ -2 \end {pmatrix} = \begin {pmatrix} 3{,}5 \\ 0 \\ 2 \end {pmatrix}\]
Nachweisen, dass \(F\) der Mittelpunkt des Umkreises ist:
\[A\,(1|7|3)\,, \quad B\,(6|-7|1)\,, \quad C\,(-2|1|-3)\,, \quad F\,(3{,}5|0|2)\]
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\vert \overrightarrow{FA} \vert = \left| \begin{pmatrix} 1 \\ 7 \\ 3 \end{pmatrix} - \begin{pmatrix} 3{,}5 \\ 0 \\ 2 \end{pmatrix} \right| = \left| \begin{pmatrix} 2{,}5 \\ 7 \\ 1 \end{pmatrix} \right| = \sqrt{2{,}5^2 + 7^2 + 1^2} = 7{,}5 \]
\[\vert \overrightarrow{FB} \vert = \left| \begin{pmatrix} 6 \\ -7 \\ 1 \end{pmatrix} - \begin{pmatrix} 3{,}5 \\ 0 \\ 2 \end{pmatrix} \right| = \left| \begin{pmatrix} 2{,}5 \\ -7 \\ -1 \end{pmatrix} \right| = \sqrt{2{,}5^2 + (-7)^2 + (-1)^2} = 7{,}5 \]
\[\vert \overrightarrow{FC} \vert = \left| \begin{pmatrix} -2 \\ 1 \\ -3 \end{pmatrix} - \begin{pmatrix} 3{,}5 \\ 0 \\ 2 \end{pmatrix} \right| = \left| \begin{pmatrix} -5{,}5 \\ 1 \\ -5 \end{pmatrix} \right| = \sqrt{(-5{,}5)^2 + 1^2 + (-5)^2} = 7{,}5 \]
\[\Longrightarrow \quad \overline{FA} = \overline{FB} = \overline{FC} = r = 7{,}5\]
\(\Longrightarrow \quad\) Der Kegel, den der Umkreis des Dreiecks \(ABC\) mit dem Punkt \(S\) festlegt, ist ein gerader Kegel.
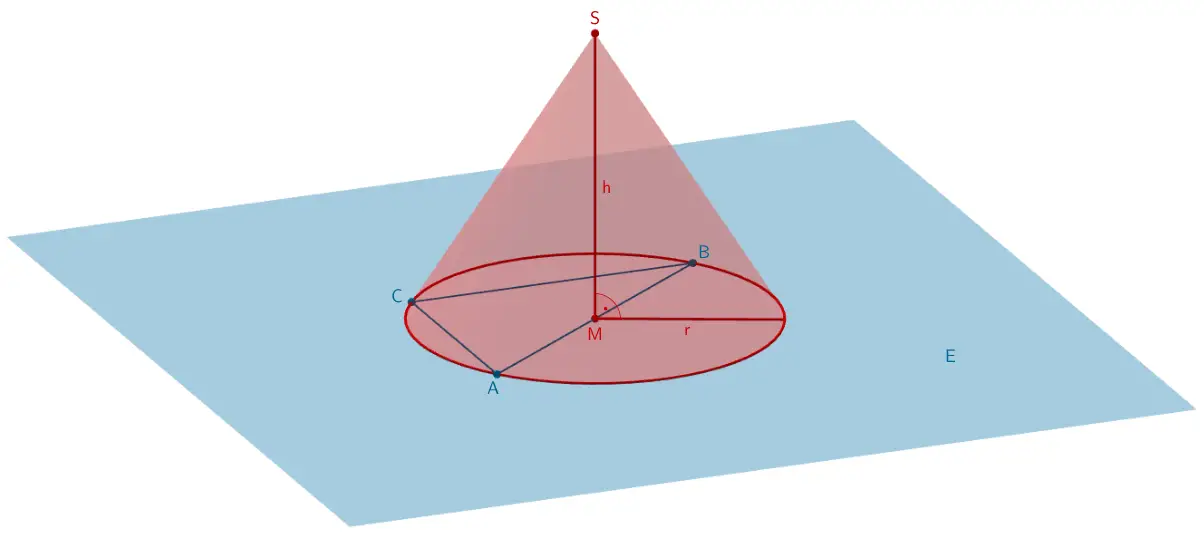
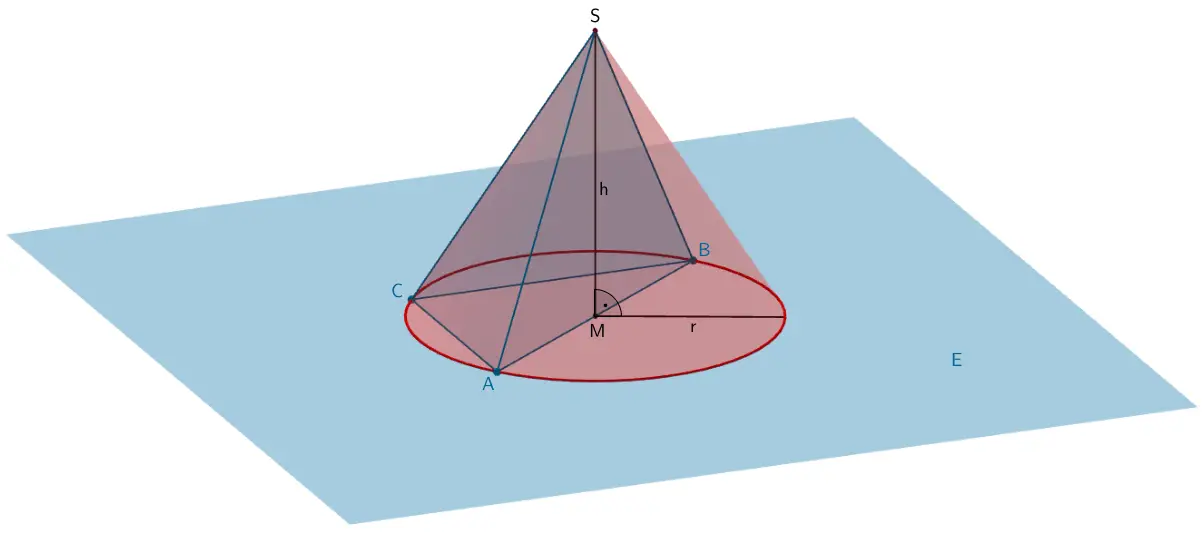
Größenvergleich: Volumen des Kegels - Volumen der Pyramide \(ABCS\)
Volumen des Kegels:
Volumen eines geraden Kreiskegels
\[V = \frac{1}{3}r^{2} \pi h\]
(vgl. Merkhilfe)
\[V_{\text{Kegel}} = \frac{1}{3} \cdot r^2 \pi \cdot \overline{MS}\]
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\overline{MS} = \vert \overrightarrow{MS} \vert = \left| \begin {pmatrix} 8 \\ 4 \\ -8 \end {pmatrix} \right| = \sqrt{(8^2 + 4^2 + (-8)^2} = 12\]
\[V_{\text{Kegel}} = \frac{1}{3} \cdot 7{,}5^2 \pi \cdot 12 = 225 \pi\]
\(V_{ABCS} = 216\) (siehe Teilaufgabe d)
\[\frac{V_{\text{Kegel}} - V_{ABCS}}{V_{ABCS}} = \frac{225 \pi - 216}{216} \approx 2{,}27 = 227 \%\]
Das Volumen des Kegels, den der Umkreis \(k\) des Dreiecks \(ABC\) mit dem Punkt \(S\) festlegt, ist ca. \(227 \; \%\) größer als das Volumen der Pyramide \(ABCS\).