Mathematik Abitur Bayern 2011 G8 Stochastik I - Aufgaben mit Lösungen

Ein Investor plant, in einer Gemeinde, die aus den Orten Oberberg und Niederberg bestehen, eine Windkraftanlage zu errichten.

Um sich einen Überblick darüber zu verschaffen, wie die Einwohner zu diesem Vorhaben stehen, beschließt der Gemeinderat, eine Umfrage unter den Wahlberechtigten der Gemeinde durchzuführen. In Niederberg werden 1722, in Oberberg 258 Einwohner befragt. 1089 aller Befragten äußern keine Einwände gegen die Windkraftanlage, darunter sind allerdings nur 27 Einwohner von Oberberg. Die übrigen befragten Personen sprechen sich gegen die Windkraftanlage aus.

Bestimmen Sie jeweils den prozentualen Anteil der Gegner der Windkraftanlage unter den Befragten von Niederberg und unter den Befragten von Oberberg.

(4 BE)

Aus allen Befragten wird zufällig eine Person ausgewählt.

Ermitteln Sie

• die Wahrscheinlichkeit \(p_1\) dafür, dass die ausgewählte Person in Oberberg wohnt und sich gegen die Windkraftanlage aussprach.

• die Wahrscheinlichkeit \(p_2\) dafür, dass die ausgewählte Person in Oberberg wohnt, wenn bekannt ist, dass sie sich gegen die Windkraftanlage aussprach.

(4 BE)

Begründen Sie, dass kein Ergebnis der Umfrage denkbar ist, bei dem \(p_1 > p_2\) ist.

(2 BE)

Die Windkraftgegner schließen sich zu einer Bürgerinitiative zusammen.

Zur Verbesserung ihrer finanziellen Mittel hat die Bürgerinitiative auf dem Gemeindefest ein Glücksrad mit zehn gleich großen Sektoren aufgebaut (vgl. Abbildung). Ein Spiel besteht aus dem einmaligen Drehen des Glücksrads; die erzielte Zahl gibt die Kategorie des Preises an, den der Spieler erhält.

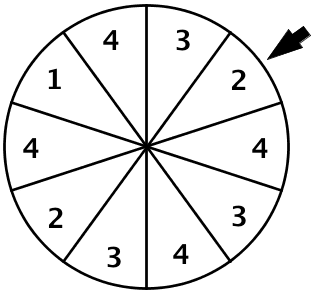
Ein Preis der Kategorie 1 ist für die Bürgerinitiative mit Unkosten in Höhe von zehn Euro, ein Preis der Kategorie 2 mit Unkosten in Höhe von fünf Euro verbunden. Preise der Kategorie 3 und 4 werden von Sponsoren gestellt und verursachen keine Unkosten. Bestimmen Sie den im Mittel pro Spiel zu erwartenden Gewinn der Bürgerinitiative, wenn der Einsatz für ein Spiel 2,50 Euro beträgt und keine weiteren Unkosten anfallen.

(5 BE)

Zehn Besucher des Gemeindefests drehen nacheinander jeweils einmal das Glücksrad. Geben Sie zu jedem der folgenden Ereignisse einen Term an, mit dem sich die Wahrscheinlichkeit des Ereignisses berechnen lässt.

\(A\): "Nur die ersten fünf Preise entfallen auf die Kategorie 4."

\(B\): "Genau die Hälfte der Preise entfällt auf die Kategorie 4."

\(C\): "Die Preise verteilen sich jeweils zur Hälfte auf die Kategorien 1 und 4."

(5 BE)

Die Bürgerinitiative veranstaltet am viel besuchten Badesee der Gemeinde eine Unterschriftenaktion gegen die geplante Windkraftanlage.

Berechnen Sie, wie hoch der Anteil \(p\) der Gegner der Windkraftanlage unter den Badegästen mindestens sein muss, damit sich unter zehn zufällig ausgewählten Badegästen mit einer Wahrscheinlichkeit von mindestens 99 % wenigstens ein Gegner der Windkraftanlage befindet. 

(5 BE)

Aufgrund der vielfältigen Aktivitäten der Bürgerinitiative vermutet der Gemeinderat, dass inzwischen mindestens 55 % der Wahlberechtigten der Gemeinde gegen die Einrichtung der Windkraftanlage sind. Um diese Vermutung zu testen, werden 200 zufällig ausgewählte Wahlberechtigte der Gemeinde befragt. Wie muss die Entscheidungsregel mit einem möglichst großen Ablehnungsbereich lauten, wenn die Vermutung des Gemeinderats mit einer Wahrscheinlichkeit von höchstens 5 % irrtümlich abgelehnt werden soll?

(5 BE)