Teilaufgabe 1f

Analysis I - Teil 2

Einen Kommentar verfassen

Begründen Sie, dass \(f\) in \(\mathbb R\) umkehrbar ist. Geben Sie den Definitionsbereich und den Wertebereich der Umkehrfunktion \(f^{-1}\) an und zeichnen Sie den Graphen von \(f^{-1}\) in Abbildung 2 ein.

(6 BE)

Lösung zu Teilaufgabe 1f

Umkehrbarkeit der Funktion \(f\)

Kriterien für die Umkehrbarkeit einer Funktion

Kriterien für die Umkehrbarkeit einer Funktion

Eine Funktion \(f\,\colon\,\mapsto f(x)\) mit der Definitionsmenge \(D_{f}\) und der Wertemenge \(W_{f}\) heißt umkehrbar, falls es zu jedem \(y \in W_{f}\) genau ein \(x \in D_{f}\) mit \(f(x) = y\) gibt.

Ist eine Funktion auf Ihrer Definitionsmenge oder einer Teilmenge streng monoton (steigend oder fallend), so ist sie dort umkehrbar.

Aus Teilaufgabe 1c ist bekannt, dass \(G_f\) in \(\mathbb R\) streng monoton steigend ist. Folglich ist \(f\) umkehrbar.

Definitionsbereich und Wetebereich der Umkehrfunktion \(f^{-1}(x)\)

Umkehrfunktion

Umkehrfunktion \(\boldsymbol{f^{-1}}\) einer Funktion \(\boldsymbol{f}\)

Bestimmung des Funktionsterms \(\boldsymbol{f^{-1}(x)}\)

1. Funktionsgleichung \(\,y = f(x)\,\) nach \(\,x\,\) auflösen

2. Variablen tauschen: \(\;x \longleftrightarrow y \quad \Longrightarrow \quad y = f^{-1}(x)\)

Es gilt: \(\;D_{f^{-1}} = W_f\;\) und \(\; W_{f^{-1}} = D_f\)

Graph der Umkehrfunktion

Die Graphen einer Funktion und ihrer Umkehrfunktion sind zueinander symmetrisch bzgl. der Winkelhalbierenden des I. und III. Quadranten mit der Gleichung \(y = x\).

Aus den Teilaufgaben 1b,c ist bekannt: \(\,D_f = \mathbb R\,\) und \(\,W_f = \; ]0;2[\,\).

\[D_{f^{-1}} = W_f = \; ]0;2[\]

\[W_{f^{-1}} = D_f = \mathbb R\]

Einzeichnen des Graphen von \(f^{-1}\)

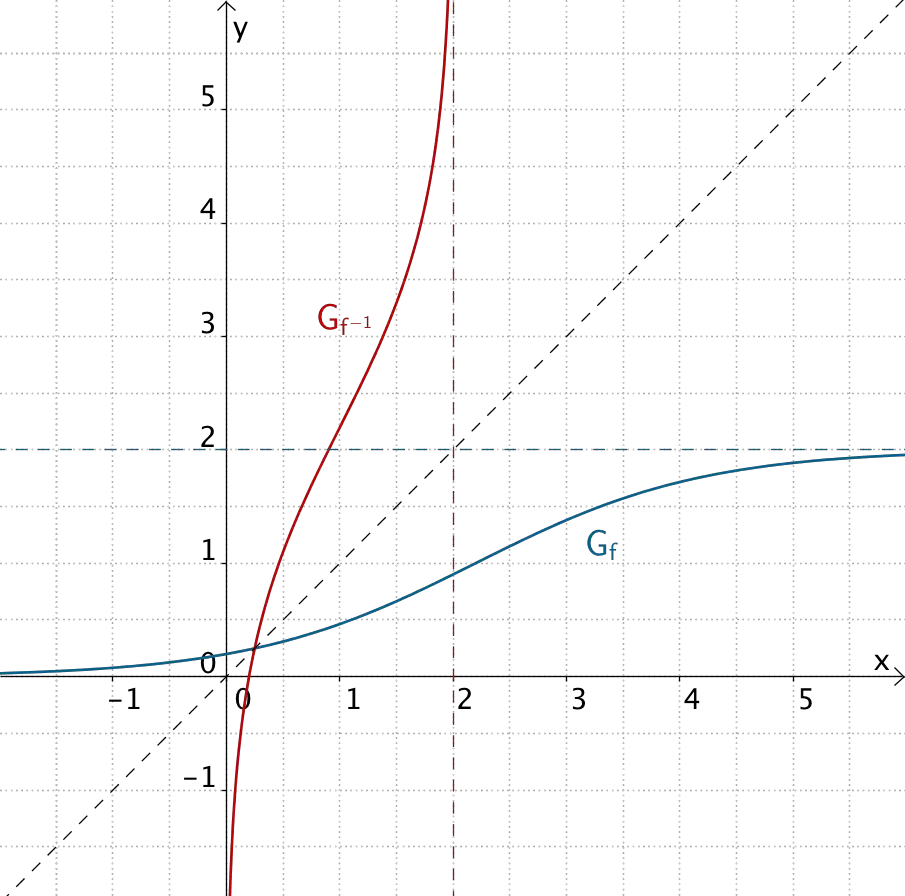
Graph der Funktion f und Graph der Umkehrfunktion fˉ¹

Graph der Funktion \(\,f\,\) und Graph der Umkehrfunktion \(\,f^{-1}\)

Alles für Dein erfolgreiches Mathe Abi Bayern