Teilaufgabe 3b
Lösung zu Teilaufgabe 3b
\[h(x) = -\ln x + 3\,; \quad D_h = \mathbb R^+\]
\[P\,(1|h(1))\]
1. Lösungsansatz: Tangentengleichung
\[T\,\colon y = h'(x_{0}) \cdot (x - x_{0}) + h(x_{0})\]
\[x_0 = 1\]
\[h(x_0) = h(1) = - \ln 1 + 3 = 3\]
Erste Ableitung \(h'\) bilden:
\[h(x) = -\ln x + 3 \quad \Longrightarrow \quad h'(x) = -\frac{1}{x}\]
\[h'(x_0) = h'(1) = -\frac{1}{1} = -1\]
\[\begin{align*} y &= h'(x_{0}) \cdot (x - x_{0}) + h(x_{0}) \\[0.8em] &= (-1) \cdot (x - 1) + 3 \\[0.8em] &= -x + 4 \end{align*}\]
\[\Longrightarrow \quad T\,\colon\, y = -x + 4\]
2. Lösungsansatz: Allgemeine Geradengleichung
\[T\,\colon\,y = m_{T} \cdot x + t\,; \quad P\,(1|h(1))\]
Tangentensteigung bestimmen:
\(\displaystyle h'(x) = -\frac{1}{x}\,\) (siehe oben)
\[m_{T} = h'(1) = -\frac{1}{1} = -1 \]
\(y\)-Achsenabschnitt \(t\) der Tangente bestimmen:
\[T\,\colon\,y = -x + t\]
\[h(1) = -\ln 1 + 3 = 3 \quad \Longrightarrow \quad P\,(1|3)\]
\[\begin{align*} P \in T\,\colon\, & & 3 &= (-1) \cdot 1 + t \\[0.8em] & & 3 &= -1+ t & &| + 1 \\[0.8em] & & 4 &= t \end{align*}\]
\[\Longrightarrow \quad T\,\colon\, y = -x + 4\]
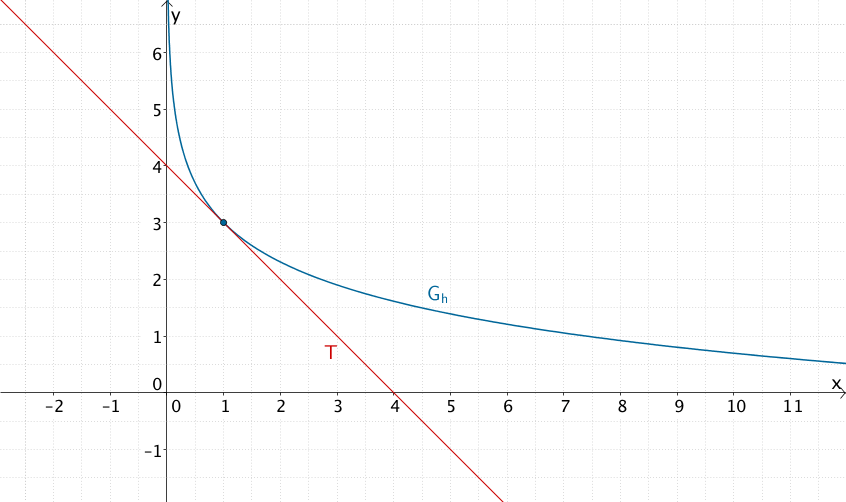
Tangente \(T\) an den Graphen der Funktion \(h\) im Punkt \((1|3)\)
