Unter dem Wasserdurchfluss eines Bachs an einer bestimmten Stelle versteht man das Volumen des Wassers, das an der Stelle in einer bestimmten Zeit vorbeifließt. Die Funktion \(f\) beschreibt die zeitliche Entwicklung des Wasserdurchflusses eines Bachs an einer Messstelle, nachdem zum Zeitpunkt \(t = 0\) eine bachaufwärts gelegene Schleuse geöffnet wurde. Abbildung 3 zeigt den Graphen \(G_f\) von \(f\,\).
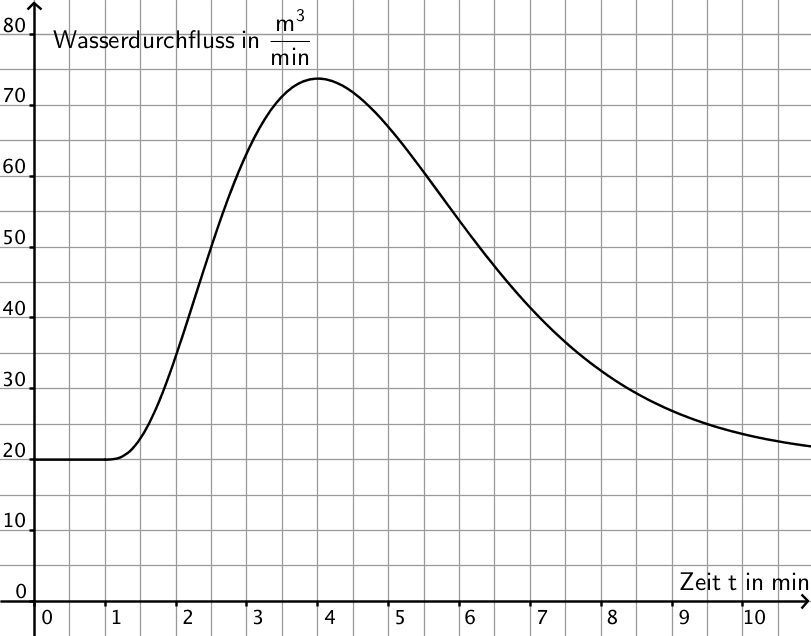
Abb. 3
Entnehmen Sie Abbildung 3 im Bereich \(t > 1\) Näherungswerte für die Koordinaten des Hochpunkts sowie für die \(t\)-Koordinaten der beiden Wendepunkte von \(G_f\) und geben Sie unter Berücksichtigung dieser Näherungswerte die jeweilige Bedeutung der genannten Punkte im Sachzusammenhang an.
(5 BE)
Lösung zu Teilaufgabe 2a
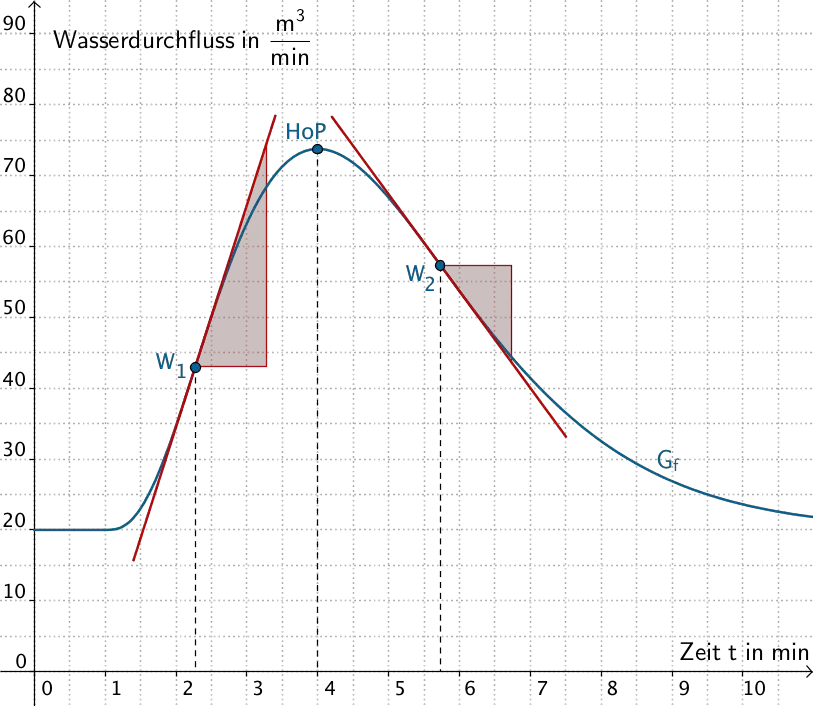
An der Wendestelle einer Funktion ändert der Funktionsgraph sein Krümmungsverhalten. Die Steigung der Tangente an eine Funktion im Wendepunkt ist - abhängig vom Krümmungsverhalten des Funktionsgraphen - maximal oder minimal. Wendepunkte entsprechen Hoch- bzw. Tiefpunkten der Ableitung einer Funktion, d.h. die lokale (momentane) Änderungsrate einer Funktion erreicht an den Wendestellen ein Maximum oder ein Minimum.
Näherungswerte: Koordinaten des Hochpunkts, Wendestellen
Im Rahmen der Ablesegenauigkeit lassen sich folgende Näherungswerte entnehmen:
\[HoP\,(4\, \pm\, 0{,}1\,|\, 74\, \pm\, 1)\]
\[t_{W_1} \approx 2{,}3\, \pm\, 0{,}2\]
\[t_{W_2} \approx 5{,}7\, \pm\, 0{,}2\]
Bedeutung im Sachzusammenhang
Bedeutung des Hochpunkts:
Zum Zeitpunkt \(t \approx 4 \:\text{min}\) nach dem Öffnen der Schleuse ist der Wasserdurchfluss des Baches an der Meßstelle mit 74 \(\frac{\text{m}^3}{\text{min}}\) am höchsten.
Bedeutung des Wendepunkts \(W_1\,\):
Zum Zeitpunkt \(t_{W_1} \approx 2{,}3 \;\text{min}\) nach dem Öffnen der Schleuse ist die Zunahme des Wasserdurchflusses an der Meßstelle am größten.
Die Steigung der Wendetangente beschreibt die maximale momentane Zunahme des Wasserdurchflusses (Einheit: \(\,\frac{\text{m}^3}{\text{min}^2}\)).
Bedeutung des Wendepunktes \(W_2\,\):
Zum Zeitpunkt \(t_{W_2} \approx 5{,}7\;\text{min}\) nach dem Öffnen der Schleuse ist die Abnahme des Wasserdurchflusses an der Meßstelle am größten.
Die Steigung der Wendetangente beschreibt die maximale momentane Abnahme des Wasserdurchflusses (Einheit: \(\,\frac{\text{m}^3}{\text{min}^2}\)).


