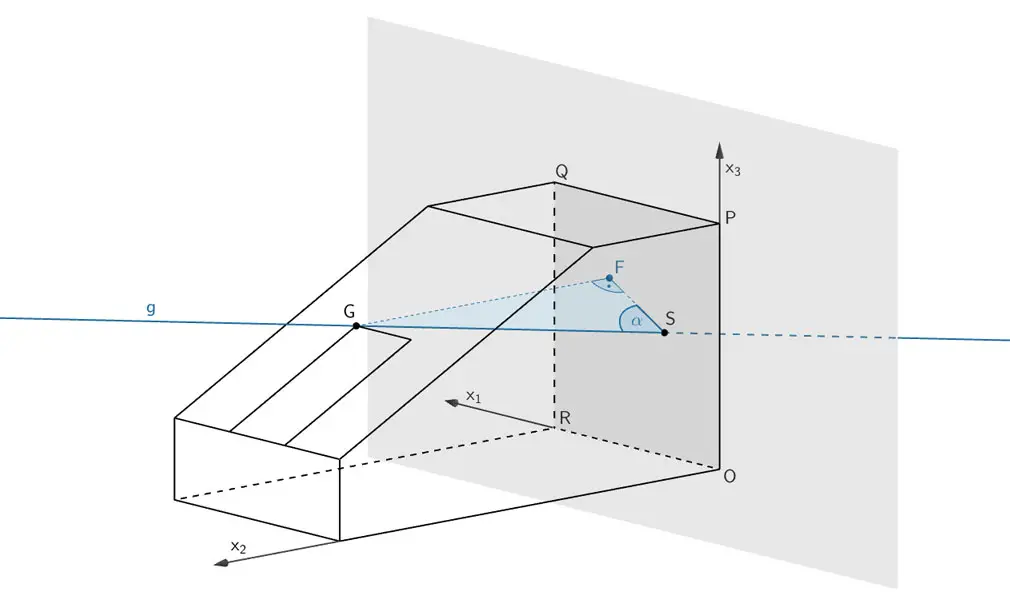
Durch das Fenster einfallendes Sonnenlicht wird im Zimmer durch parallele Geraden mit dem Richtungsvektor \(\overrightarrow v = \begin{pmatrix} -2 \\ -8 \\ -1 \end{pmatrix}\) repräsentiert. Eine dieser Geraden verläuft durch den Punkt \(G\) und schneidet die Seitenwand \(OPQR\) im Punkt \(S\). Berechnen Sie die Koordinaten von \(S\) sowie die Größe des Winkels, den diese Gerade mit der Seitenwand \(OPQR\) einschließt.
(6 BE)
Lösung zu Teilaufgabe d
Koordinaten des Schnittpunktes \(S\)
Lagebeziehung von Gerade und Ebene
| \(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}; \; \lambda \in \mathbb R \enspace\) und \(\enspace E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{B}) = 0\) | |||
| \(\overrightarrow{u} \circ \overrightarrow{n}_{E} = 0 \enspace \Longleftrightarrow \enspace \overrightarrow{u} \perp \overrightarrow{n}_{E}\) | \(\overrightarrow{u} \circ \overrightarrow{n}_{E} \neq 0\) | ||
|
\(A \in E\) \(\Longrightarrow \enspace g \subset E\) \(g\) liegt in der Ebene \(E\)
|
\(A \notin E\) \(\Longrightarrow \quad g \parallel E\) \(g\) verläuft (echt) parallel zur Ebene \(E\) (ggf. Abstand berechnen).
|
\(\Longrightarrow \enspace\)\(g\) schneidet die Ebene \(E\) im Schnittpunkt \(S\) unter dem Schnittwinkel \(\alpha\) (ggf. Schnittpunkt und/oder Schnitwinkel berechnen). |
|
Es sei \(g\) die Gerade mit dem Richtungsvektor \(\overrightarrow{v} = \begin{pmatrix} -2 \\ -8 \\ -1 \end{pmatrix}\) und dem Aufpunkt \(G\,(2|4|2)\).
\[g \colon \enspace \overrightarrow{X} = \begin{pmatrix} 2 \\ 4 \\ 2 \end{pmatrix} + \mu \cdot \begin{pmatrix} -2 \\ -8 \\ -1 \end{pmatrix}\,, \quad \mu \in \mathbb R\]
Die Seitenwand \(OPQR\) liegt in der \(x_1x_3\)-Ebene:
\[OPQR \subset x_1x_3\text{-Ebene}\,, \qquad x_1x_3\text{-Ebene}\, \colon \enspace x_2 = 0\]
Zur Berechnung des Schnittpunktes \(S\) setzt man die \(x_2\)-Koordinate des Ortsverktors \(\overrightarrow X\) aus der Geradengleichung von \(g\) in die Normalengleichung der \(x_1x_3\)-Ebene ein und löst die Gleichung nach dem Parameter \(\mu\) auf.
\[\begin{align*} g \cap x_1x_3\text{-Ebene} \, \colon \enspace 4 - 8\mu &= 0 & &| +8\mu \\[0.8em] 4 &= 8\mu & &| : 8 \\[0.8em] \mu &= \frac{1}{2} \end{align*}\]
Parameterwert \(\mu = \frac{1}{2}\) in \(g\) einsetzen:
\[S \in g \, \colon \enspace \overrightarrow{S} = \begin{pmatrix} 2 \\ 4 \\ 2 \end{pmatrix} + \frac{1}{2} \cdot \begin{pmatrix} -2 \\ -8 \\ -1 \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ 1{,}5 \end{pmatrix} \quad \Longrightarrow \quad S\,(1|0|1{,}5)\]
Schnittwinkel der Gerade mit der Seitenwand \(OPQR\)
Das Lot des Punktes \(\,G\,\) auf die \(x_1x_3\)-Ebene legt den Lotfußpunkt \(\,F\,\) fest. Der Schnittwinkel \(\,\alpha\,\) ist definiert als der Winkel \(\,FSG\,\) im rechtwinkligen Dreieck \(\,GSF\,\).
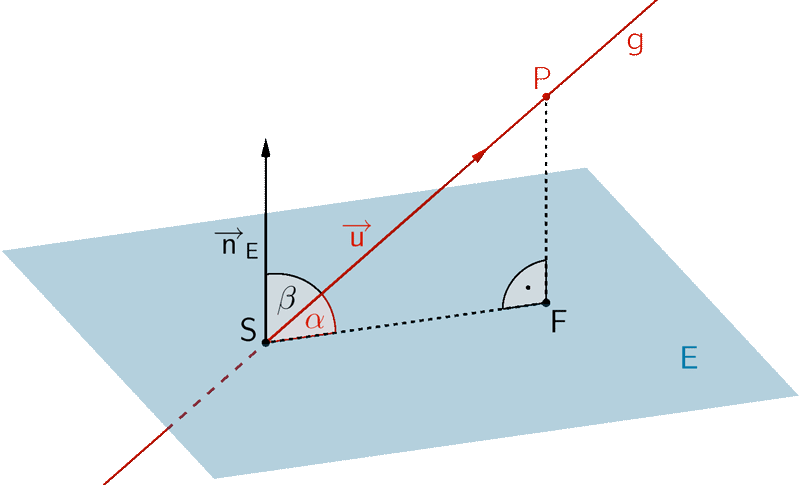
Schnittwinkel \(\boldsymbol{\alpha}\) zwischen Gerade und Ebene
Für \(0^{\circ} \leq \alpha \leq 90^{\circ}\) und \(0^{\circ} \leq \beta \leq 90^{\circ}\) gilt:
\[\begin{align*} \cos \beta &= \frac{\vert \overrightarrow{u} \circ \overrightarrow{n}_{E} \vert}{\vert \overrightarrow{u} \vert \cdot \vert \overrightarrow{n}_{E} \vert} \enspace \Rightarrow \enspace \beta = \cos^{-1}(\dots) \\[0.8em] \alpha &= 90^{\circ} - \beta \end{align*}\]
\[\sin \alpha = \frac{\vert \overrightarrow{u} \circ \overrightarrow{n}_{E} \vert}{\vert \overrightarrow{u} \vert \cdot \vert \overrightarrow{n}_{E} \vert} \enspace \Rightarrow \enspace \alpha = \sin^{-1}(\dots)\]
Richtungsvektor der Geraden \(g\,\): \(\enspace \overrightarrow{v} = \begin{pmatrix} -2 \\ -8 \\ -1 \end{pmatrix}\)
Nornmalenvektor der \(x_1x_3\)-Ebene: \(\enspace \overrightarrow{n}_{x_1x_3} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}\)
Schnittwinkel \(\alpha\) berechnen:
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin{align*} \sin \alpha &= \frac{\vert \overrightarrow{v} \circ \overrightarrow{n}_{x_1x_3} \vert}{\vert \overrightarrow{v}^{\,*} \vert \cdot \vert \overrightarrow{n}_{x_1x_3} \vert} \\[0.8em] &= \frac{\left| \begin{pmatrix} -2 \\ -8 \\ -1 \end{pmatrix} \circ \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} \right|}{\left| \begin{pmatrix} -2 \\ -8 \\ -1 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} \right|} \\[0.8em] &= \frac{\vert (-2) \cdot 0 + (-8) \cdot 1 + (-1) \cdot 0 \vert}{\sqrt{(-2)^2 + (-8)^2 + (-1)^2} \cdot \sqrt{0^2 + 1^2 + 0^2}} \\[0.8em] &= \frac{8}{\sqrt{69}} & &| \; \sin^{-1}(\dots) \\[1.6em] \alpha &\approx 74{,}4^{\circ} \end{align*}\]