Teilaufgabe 4a

Lösung zu Teilaufgabe 4a

 

Wahrscheinlichkeit von Ereignis \(A\)

 

Ereignis \(A\,\): "Bei einer Aufführung wird der Vorhang kein einziges Mal von Hand zugezogen."

 

Binomialverteilung

Möglichkeit a: "Schließen des Vorhangs von Hand" als Treffer festlegen

 

Zufallsgröße \(X \colon \enspace\) "Anzahl der Schließungen des Vorhangs von Hand"

 

Analyse der Angabe:

 

"Bei jeder Aufführung wird der Vorhang 15-mal geschlossen; ..."

\[\Longrightarrow \quad n = 15\]

 

"Erfahrungsgemäß funktioniert der Mechanismus ... mit einer Wahrscheinlichkeit von 90 %."

\(\Longrightarrow \quad\) Automatisches Schließen: \(\,p = 0{,}9\,\), Schließen von Hand: \(\,p = 0{,}1\)

 

\(A\,\): "Bei einer Aufführung wird der Vorhang kein einziges Mal von Hand zugezogen."

\[\Longrightarrow \quad X = 0\]

 

Die Zufallsgröße \(X\) ist nach \(B(15;0{,}1)\) binomialverteilt.

 

\[\Longrightarrow \quad P(A) = P^{15}_{0{,}1}(X = 0)\]

 

Stochastisches Tafelwerk (ST) verwenden:

 

\[P(A) = P^{15}_{0{,}1}(X = 0) = B(15;0{,}1;0) \enspace \overset{\text{ST}}{=} \enspace 0{,}20589 \approx 20{,}6\,\%\]

 

Alternative: Anwenden der Formel von Bernouli:

\[\begin{align*}P(A) &= P^{15}_{0{,}1}(X = 0) = B(15;0{,}1;0) \\[0.8em] &= \underbrace{\binom{15}{0}}_{1} \cdot \underbrace{0{,}1^0}_{1} \cdot (1 - 0{,}1)^{15 - 0} \\[0.8em] &\approx 0{,}206 = 20{,}6\,\% \end{align*}\]

 

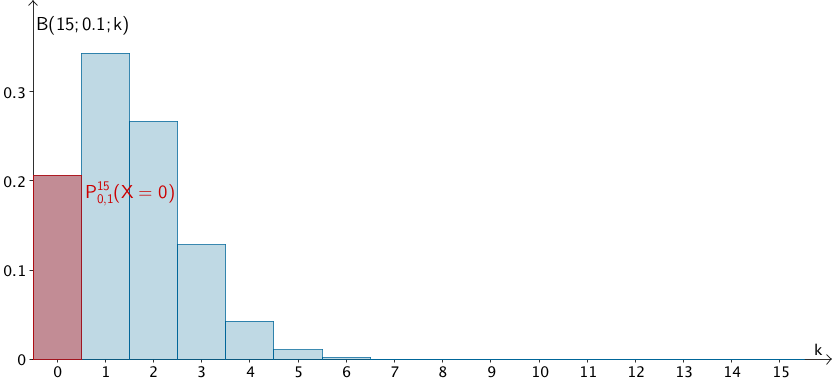
Wahrscheinlichkeitsverteilung der nach \(\,B(15;0{,}1)\,\) binomialverteilten Zufallsgöße \(\,X \colon \enspace\) "Anzahl der Schließungen des Vorhangs von Hand"

 

Möglichkeit b: "Automatisches Schließen des Vorhangs" als Treffer festlegen

 

Zufallsgröße \(Y\colon \enspace\) "Anzahl der automatischen Schließungen des Vorhangs"

 

Automatisches Schließen: \(\,p = 0{,}9\) (Trefferwarscheinlichkeit)

15 Schließversuche: \(n = 15\)

Fünfzehnmal automatisches Schließen: \(Y = 15\)

 

Die Zufallsgröße \(Y\) ist nach \(B(15; 0{,}9)\) binomialverteilt.

 

\[\Longrightarrow \quad P(A) = P^{15}_{0{,}9}(Y = 15)\]

 

Stochastisches Tafelwerk (ST) verwenden:

 

\[P(A) = P^{15}_{0{,}9}(Y = 15) = B(15;0{,}9;15) \enspace \overset{\text{ST}}{=} \enspace 0{,}20589 \approx 20{,}6\,\%\]

 

Alternative: Anwenden der Formel von Bernouli:

\[\begin{align*}P(A) &= P^{15}_{0{,}9}(Y = 15) = B(15;0{,}9;15) \\[0.8em] &= \underbrace{\binom{15}{15}}_{1} \cdot 0{,}9^{15} \cdot \underbrace{(1 - 0{,}9)^{15 - 15}}_{1} \\[0.8em] &\approx 0{,}206 = 20{,}6\,\% \end{align*}\]

 

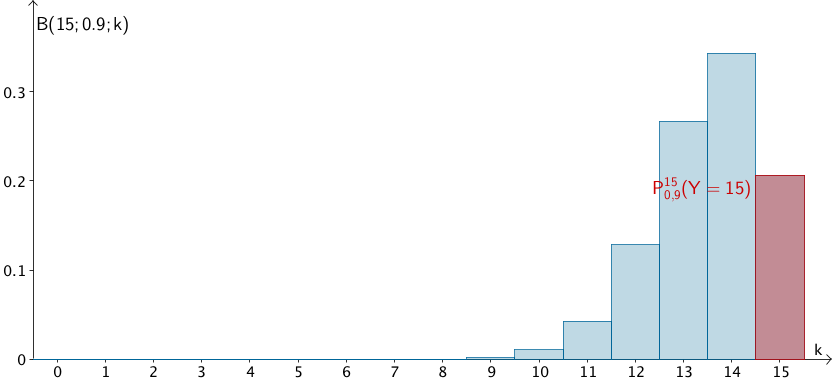
Wahrscheinlichkeitsverteilung der nach \(\,B(15;0{,}9)\,\) binomialverteilten Zufallsgöße \(\,Y \colon \enspace\) "Anzahl der automatischen Schließungen des Vorhangs"

 

Wahrscheinlichkeit von Ereignis \(B\)

 

Ereignis \(B\,\): "Bei einer Aufführung lässt sich der Vorhang zunächst viermal automatisch schließen, insgesamt wird der Vorhang jedoch genau zweimal von Hand zugezogen."

 

1. Lösungsansatz: Ereignis \(B\) als zwei aufeinander folgende Bernoulli-Ketten betrachten

 

Jeder Schließversuch des Vorhangs beschreibt ein Bernoulli-Experiment mit den Ergebnissen: "automatisches Schließen" und "Schließen von Hand". Das Ereignis \(B\) formuliert für die ersten vier Schließungen eine andere Bedingung als für die verbleibenden elf Schließungen:

- die ersten vier Mal soll der Vorhang automatisch schließen,

- bei den folgenden elf Schließversuchen soll der Vorhang zweimal von Hand schließen.

Somit kann das Ereignis \(B\) als zwei aufeinander folgende Bernoulli-Ketten betrachtet werden, für die jeweils das Ergebnis "automatisches Schließen" oder das Ergebnis " Schließen von Hand" als Treffer festzulegen ist.

 

Zufallsgröße \(X \colon \enspace\) "Anzahl der Schließungen des Vorhangs von Hand"

Zufallsgröße \(Y\colon \enspace\) "Anzahl der automatischen Schließungen des Vorhangs"

 

Betrachten der ersten vier Schließversuche

Vier Schließversuche: \(n = 4\)

Schließen von Hand: \(p = 0{,}1\) (Trefferwahrscheinlichkeit)

Kein Schließen von Hand unter den ersten vier Schließversuchen: \(X = 0\)

 

Die Zufallsgröße \(X\) ist nach \(B(4;0{,}1)\) binomialverteilt.

 

oder:

 

Vier Schließversuche: \(n = 4\)

Automatisches Schließen: \(p = 0{,}9\) (Trefferwahrscheinlichkeit)

Viermal automatisches Schließen: \(Y = 4\)

 

Die Zufallsgröße \(Y\) ist nach \(B(4;0{,}9)\) binomialverteilt.

 

\[\Longrightarrow \quad P_{0{,}1}^4(X = 0) = P_{0{,}9}^4(Y = 4)\]

 

Betrachten der verbleibenden elf Schließversuche

Elf Schließversuche: \(n = 11\)

Schließen von Hand: \(p = 0{,}1\) (Trefferwahrscheinlichkeit)

Zweimal Schließen von Hand unter den verbeibenden elf Schließversuchen: \(X = 2\)

 

Die Zufallsgröße \(X\) ist nach \(B(11;0{,}1)\) binomialverteilt.

 

oder:

 

Elf Schließversuche: \(n = 11\)

Automatisches Schließen: \(p = 0{,}9\) (Trefferwahrscheinlichkeit)

Neunmal automatisches Schließen unter den verbleibenden elf Schließversuchen: \(Y = 9\)

 

Die Zufallsgröße \(Y\) ist nach \(B(11;0{,}9)\) binomialverteilt.

 

\[\Longrightarrow \quad P_{0{,}1}^{11}(X = 2) = P_{0{,}9}^{11}(Y = 9)\]

 

Damit ergeben sich folgende vier Möglichkeiten, um die Wahrscheinlichkeit des Ereignisses \(B\) zu errechnen:

0 mal Schießen von Hand bei den ersten 4 Schließversuchen von 2 mal Schließen von Hand bei den verbleibenden 11 Schließversuchen:

\[\begin{align*} P(B) &= \underbrace{P_{0{,}1}^4(X = 0)}_{n = 4} \cdot \underbrace{P_{0{,}1}^{11}(X = 2)}_{n = 11} \\[0.8em] &= \left[\binom{4}{0} \cdot 0{,}1^0 \cdot (1 - 0{,}1)^{4 - 0}\right] \cdot \left[\binom{11}{2} \cdot 0{,}1^2 \cdot (1 - 0{,}1)^{11 - 2}\right] \\[0.8em] &= \left[0{,}9^4\right] \cdot \left[55 \cdot 0{,}1^2 \cdot 0{,}9^9\right] \\[0.8em] &\approx 0{,}14 = 14\,\%\end{align*}\]

 

4 mal automatisches Schießen bei den ersten 4 Schließversuchen von 9 mal automatisches Schließen bei den verbleibenden 11 Schließversuchen:

\[\begin{align*} P(B) &= \underbrace{P_{0{,}9}^4(Y = 4)}_{n = 4} \cdot \underbrace{P_{0{,}9}^{11}(Y = 9)}_{n = 11} \\[0.8em] &= \left[\binom{4}{4} \cdot 0{,}9^4 \cdot (1 - 0{,}9)^{4 - 4}\right] \cdot \left[\binom{11}{9} \cdot 0{,}9^9 \cdot (1 - 0{,}9)^{11 - 9}\right] \\[0.8em] &= \left[0{,}9^4\right] \cdot \left[55 \cdot 0{,}9^9 \cdot 0{,}1^2\right] \\[0.8em] &\approx 0{,}14 = 14\,\%\end{align*}\]

 

0 mal Schießen von Hand bei den ersten 4 Schließversuchen von 9 mal Schließen von Hand bei den verbleibenden 11 Schließversuchen:

\[\begin{align*} P(B) &= \underbrace{P_{0{,}1}^4(X = 0)}_{n = 4} \cdot \underbrace{P_{0{,}9}^{11}(Y = 9)}_{n = 11} \\[0.8em] &= \left[\binom{4}{0} \cdot 0{,}1^0 \cdot (1 - 0{,}1)^{4 - 0}\right] \cdot \left[\binom{11}{9} \cdot 0{,}9^9 \cdot (1 - 0{,}1)^{11 - 9}\right] \\[0.8em] &= \left[0{,}9^4\right] \cdot \left[55 \cdot 0{,}9^9 \cdot 0{,}1^2\right] \\[0.8em] &\approx 0{,}14 = 14\,\%\end{align*}\]

 

4 mal automatisches Schießen bei den ersten 4 Schließversuchen von 2 mal Schließen von Hand bei den verbleibenden 11 Schließversuchen:

\[\begin{align*} P(B) &= \underbrace{P_{0{,}9}^4(Y = 4)}_{n = 4} \cdot \underbrace{P_{0{,}1}^{11}(X = 2)}_{n = 11} \\[0.8em] &= \left[\binom{4}{4} \cdot 0{,}9^4 \cdot (1 - 0{,}9)^{4 - 4}\right] \cdot \left[\binom{11}{2} \cdot 0{,}1^2 \cdot (1 - 0{,}1)^{11 - 2}\right] \\[0.8em] &= \left[0{,}9^4\right] \cdot \left[55 \cdot 0{,}1^2 \cdot 0{,}9^9\right] \\[0.8em] &\approx 0{,}14 = 14\,\%\end{align*}\]

 

2. Lösungsansatz: Veranschaulichung der relevanten Pfade eines Baumdiagramms

 

Betrachtung der ersten vier Schließversuche

 

Automatisches Schließen: \(\,p = 0{,}9\)

 

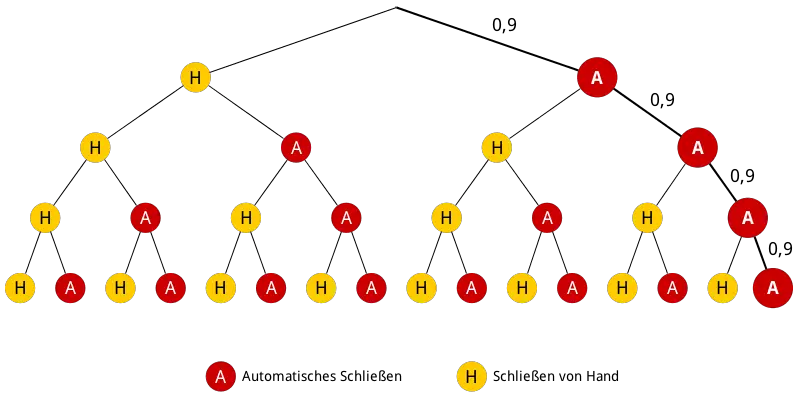
Die Abbildung zeigt das vollständige Baumdiagramm für die ersten vier Schließversuche. Der rechte Pfad beschreibt das Ereignis "Bei einer Aufführung lässt sich der Vorhang zunächst viermal automatisch schließen."

 

Anwenden der 1. Pfadregel:

\[P(\text{"Viermal A"}) = 0{,}9^4\]

 

Betrachtung der verbleibenden elf Schließungen des Vorhangs

 

Automatisches Schließen: \(p = 0{,}9\)

Schließen von Hand: \(p = 0{,}1\)

 

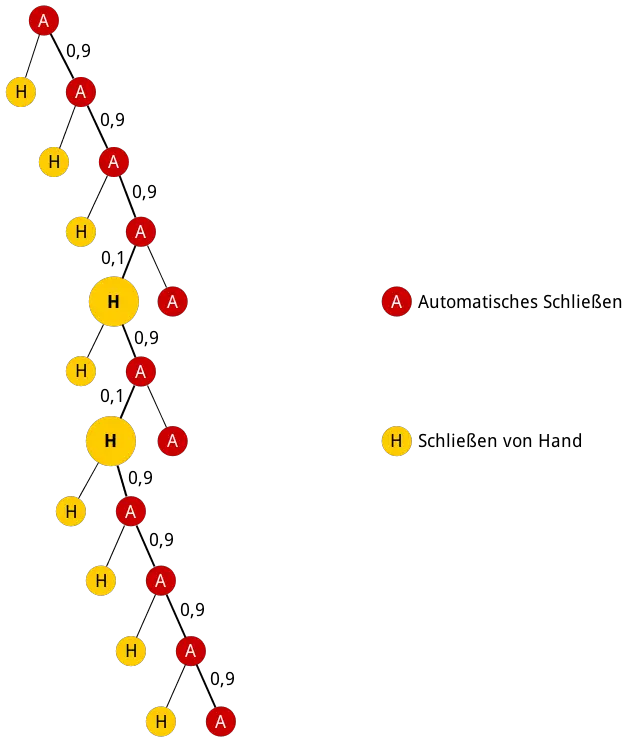
Die Abbildung zeigt einen möglichen Pfad, der ein Ergebnis des Ereignisses "Zweimal Schließen von Hand von elf verbleibenden Schließversuchen" ist.

Da die Reihenfolge der Schließergebnisse keine Rolle spielt, gibt es \(\binom{11}{2} = 55\) verschiedene Ergebnisse, die zusammen das Ereignis "Zweimal Schließen von Hand von elf verbleibenden Schließversuchen" beschreiben.

Nach der 1. Pfadregel bestimmt der Term \(0{,}1^2 \cdot 0{,}9^9\) die Wahrscheinlickeit eines der 55 Ergebnisse.

 

\[P(\text{"Zweimal H"}) = \binom{11}{2} \cdot 0{,}1^2 \cdot 0{,}9^9\]

 

Wahrscheinlichkeit \(P(B)\) berechnen:

 

\[\begin{align*}P(B) &= P(\text{"Viermal A"}) \cdot P(\text{"Zweimal H"}) \\[0.8em] &= 0{,}9^4 \cdot \binom{11}{2} \cdot 0{,}1^2 \cdot 0{,}9^9 \\[0.8em] &\approx 0{,}14 = 14\,\%\end{align*}\]