Geben Sie jeweils den Term einer in \(\mathbb R\) definierten Funktion an, die die angegebene Wertemenge \(\mathbb W\) hat.
\(\mathbb W = [-2;2]\)
(2 BE)
Lösung zu Teilaufgabe 2b
1. Lösungsansatz: Sinusfunktion oder Kosinusfunktion
Eine Sinusfunktion oder eine Kosinusfunktion, die nicht in \(y\)-Richtung verschoben ist, und deren Amplitude \(a = 2\) beträgt, ist in \(\mathbb R\) definiert und hat die Wertemenge \(W = [-2;2]\).
Allgemeine Sinusfunktion
\[f(x) = a \cdot \sin(bx + c) + d = a \cdot \sin \left[b \left(x + \frac{c}{b} \right) \right] + d\]
\[a,b,c,d \in \mathbb R\;; \quad a,b \neq 0\;; \quad x \in \mathbb R\]
Streckung um \(a\) in \(y\)-Richtung
Streckung um \(\displaystyle \frac{1}{b}\) in \(x\)-Richtung, Periode: \(\displaystyle p = \frac{2\pi}{\vert b \vert}\)
Verschiebung um \(\displaystyle -\frac{c}{b}\) in \(x\)-Richtung
Verschiebung um \(d\) in \(y\)-Richtung
\[f(x) = 2 \cdot \sin(bx + c)\]
Allgemeine Kosinusfunktion
\[f(x) = a \cdot \cos(bx + c) + d = a \cdot \cos \left[b \left(x + \frac{c}{b} \right) \right] + d\]
\[a,b,c,d \in \mathbb R\;; \quad a,b \neq 0\;; \quad x \in \mathbb R\]
Streckung um \(a\) in \(y\)-Richtung
Streckung um \(\displaystyle \frac{1}{b}\) in \(x\)-Richtung, Periode: \(\displaystyle p = \frac{2\pi}{\vert b \vert}\)
Verschiebung um \(\displaystyle -\frac{c}{b}\) in \(x\)-Richtung
Verschiebung um \(d\) in \(y\)-Richtung
\[g(x) = 2 \cdot \cos(bx + c)\]
Beispiele:
\[f(x) = 2 \cdot \sin x\]
\[g(x) = 2 \cdot \cos \left(3x + \frac{\pi}{3} \right)\]
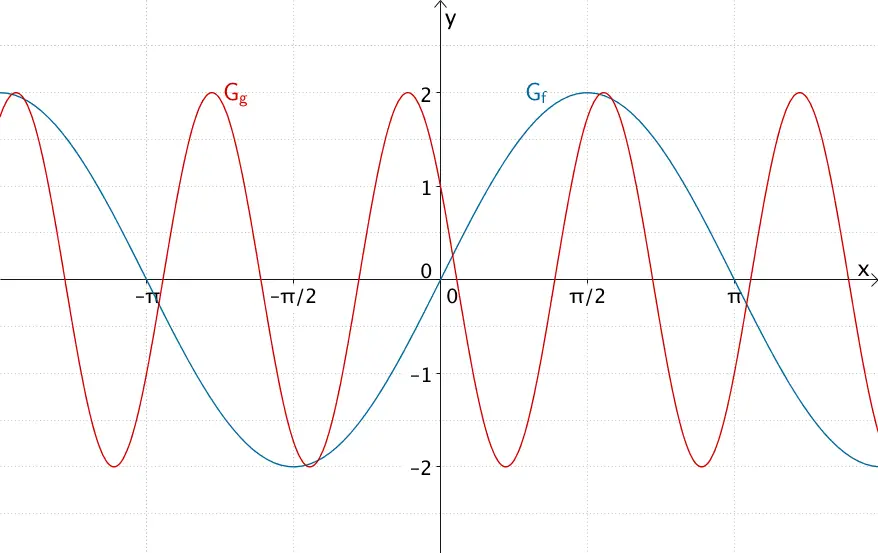
Sinusfunktion \(f\) und Kosinusfunktion \(g\) mit dem Wertebereich \(\mathbb W = [-2;2]\)
Anmerkung: Der Nachfolgende 2. Lösungsansatz erfordert ein vertieftes Verständnis der Funktionenlehre. Er orientiert sich nicht am Grundwissen eines Teil 1 des Aufgabenbereichs Analysis.
2. Lösungsansatz: Funktionen, deren absolute Extrema die Wertemenge bestimmen
Für den Ansatz wird eine gebrochenrationale Funktion \(k\) mit folgenden Eigenschaften gewählt:
- Der Graph von \(k\) hat keine Polstelle (\(D_k = \mathbb R\))
- Der Graph von \(k\) besitzt eine einfache Nullstelle (mit Vorzeichenwechsel)
- Die \(x\)-Achse ist für \(x \to \pm \infty\) waagrechte Asymptote von \(G_k\)
\[k(x) = a \cdot \frac{x}{x^2 + 1}\]
Da für den Nennerterm \(x^2 + 1 > 0\) gilt, ist die gebrochenrationale Funktion \(k\) in \(\mathbb R\) definiert. Für \(x = 0\) hat \(G_k\) eine Nullstelle mit Vorzeichenwechsel. Da der Grad des Zählerpolynoms um eins kleiner ist als der Grad des Nennerpolynoms, besitzt der Graph von \(k\) die \(x\)-Achse als waagrechte Asymptote.
Asymptoten gebrochenrationaler Funktionen
Eine Funktion \(f(x) = \dfrac{z(x)}{n(x)} = \dfrac{\textcolor{#cc071e}{a_{m}}x^{\textcolor{#cc071e}{m}} + a_{m - 1}x^{m - 1} + \dots + a_{1}x +a_{0}}{\textcolor{#0087c1}{b_{n}}x^{\textcolor{#0087c1}{n}} + b_{n - 1}x^{n - 1} + \dots + b_{1}x + b_{0}}\), die sich als Quotient zweier ganzrationaler Funktionen (Polynome) \(z(x)\) und \(n(x)\) darstellen lässt, heißt gebrochenrationale Funktion. Die Nullstellen des Nennerpolynoms \(n(x)\) können nicht in der Definitionsmenge \(D_{f}\) enthalten sein und werden als Definitionslücken bezeichnet.
Senkrechte Asymptoten
Wenn an einer Definitionslücke \(x_{0}\) einer gebrochenrationalen Funktion \(f\)
\(\begin{align*}\lim \limits_{x\,\to\,x_{0}^{-}}f(x) = +\infty \enspace &\text{oder} \enspace \lim \limits_{x\,\to\,x_{0}^{-}}f(x) = -\infty \\[0.8em] \text{und} \enspace \lim \limits_{x\,\to\,x_{0}^{+}}f(x) = +\infty \enspace &\text{oder} \enspace \lim \limits_{x\,\to\,x_{0}^{+}}f(x) = -\infty \end{align*}\)
gilt, so nennt man \(x_{0}\) eine Polstelle von \(f\) und die Gerade mit der Gleichung \(x = x_{0}\) ist senkrechte Asymptote des Graphen von \(f\).
Waagrechte und schräge Asymptoten
Der Graph einer gebrochenrationalen Funktion \(f\) hat für \(x \to - \infty\) bzw. \(x \to + \infty\) im Fall
| \(\textcolor{#cc071e}{m} < \textcolor{#0087c1}{n}\): | die \(x\)-Achse \((y = 0)\) als waagrechte Asymptote, |
| \(\textcolor{#cc071e}{m} = \textcolor{#0087c1}{n}\): | eine waagrechte Asymptote parallel zur \(\boldsymbol{x}\)-Achse mit der Gleichung \(y = \dfrac{\textcolor{#cc071e}{a_{m}}}{\textcolor{#0087c1}{b_{n}}}\), |
| \(\textcolor{#cc071e}{m} = \textcolor{#0087c1}{n} + 1\): | eine schräge Asymptote, |
| \(\textcolor{#cc071e}{m} > \textcolor{#0087c1}{n} + 1\): | keine waagrechte oder schräge Asymptote. |
\(\displaystyle \lim \limits_{x \, \to \, - \infty} \biggl( a \cdot \frac{x}{\underbrace{x^2 + 1}_{\to \, + \infty}} \biggr) = 0^- \,; \quad\) \(\displaystyle \lim \limits_{x \, \to \, + \infty} \biggl( a \cdot \frac{x}{\underbrace{x^2 + 1}_{\to \, + \infty}} \biggr) = 0^+ \,;\)
Strecken von Funktionsgraphen
Streckung in \(\textcolor{#0087c1}{x}\)-Richtung mit Streckungsfaktor \(\textcolor{#0087c1}{k}\,\):
\[h(x) = f\left(\textcolor{#0087c1}{\frac{1}{k}} \cdot x \right), \enspace k > 0\]
Streckung in \(\textcolor{#0087c1}{x}\)-Richtung mit Streckungsfaktor \(\textcolor{#0087c1}{\dfrac{1}{k}}\):
\[h(x) = f(\textcolor{#0087c1}{k} \cdot x), \enspace k > 0\]
Streckung in \(\textcolor{#cc071e}{y}\)-Richtung mit Streckungsfaktor \(\textcolor{#cc071e}{k}\,\):
\[g(x) = \textcolor{#cc071e}{k} \cdot f(x), \enspace k > 0\]
Der Faktor \(a\) bewirkt eine Streckung von \(G_k\) in \(y\)-Richtung. Er bestimmt die Lage der absoluten Extrema, welche die Wertemenge einschränken.
Symmetrieverhalten von Funktionsgraphen bzgl. des Koordinatensystems
\(f(-x) = f(x) \hspace{32px} \Longrightarrow \quad G_f\) ist achsensymmetrisch zur \(y\)-Achse
\(f(-x) = -f(x) \hspace{20px} \Longrightarrow \quad G_f\) ist punktsymmetrisch zum Ursprung
Der Graph von \(k\) ist punktsymmetrisch \(k(-x) = -k(x)\), weshalb ein absolutes Maximum und ein absolutes Minimum zu erwarten ist.
Faktor \(a\) bzw. Lage der absoluten Extrema bestimmen:
Die Wertemnge \(\mathbb W = [-2;2]\) legt die Funktionswerte an den Extremstellen \(x_{E_1}\) und \(x_{E_2}\) fest.
\[k(x_{E_1}) = -2\,; \quad k(x_{E_2}) = 2\]
oder
\[k(x_{E_1}) = 2\,; \quad k(x_{E_2}) = -2\]
Notwendige Bedingung für die Extremstellen von \(G_k\):
\[k'(x) \overset{!}{=} 0\]
1. Ableitung \(k'(x)\) bilden:
Quotientenregel
\[ f(x) = \frac{u(x)}{v(x)} \quad \Longrightarrow \quad f'(x) = \frac{u'(x) \cdot v(x) - u(x) \cdot v'(x)}{[v(x)]^2}\]
Ableitung einer Potenzfunktionen
\[ f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
(vgl. Merkhilfe)
\[k(x) = a \cdot \frac{x}{x^2 + 1}\]
\[\begin{align*}k'(x) &= a \cdot \frac{1 \cdot (x^2 + 1) - x \cdot 2x}{(x^2 + 1)^2} \\[0.8em] &= a \cdot \frac{-x^2 + 1}{(x^2 + 1)^2} \end{align*}\]
\[\begin{align*}k'(x) \overset{!}{=} 0 \quad \Longrightarrow \quad -x^2 + 1 &= 0 & &| + x^2 \\[0.8em] 1 &= x^2 & &| \; \sqrt{\quad} \\[0.8em] \pm 1 &= x_{1,2} \end{align*}\]
\[\Longrightarrow \quad x_{E_1} = -1; \quad x_{E_2} = 1\]
Faktor \(a\) berechnen:
\[\begin{align*} k(x_{E_1}) &= -2 \\[0.8em] k(-1) &= -2 \\[0.8em] a \cdot \frac{-1}{((-1)^2 + 1)} &= -2 \\[0.8em] -\frac{a}{2} &= -2 & &| \cdot (-2) \\[0.8em] a &= 4 \end{align*}\]
\[\begin{align*} k(x_{E_2}) &= 2 \\[0.8em] k(1) &= 2 \\[0.8em] a \cdot \frac{1}{(1^2 + 1)} &= 2 \\[0.8em] \frac{a}{2} &= 2 & &| \cdot 2 \\[0.8em] a &= 4 \end{align*}\]
\[\Longrightarrow \quad k_1(x) = 4 \cdot \frac{x}{(x^2 + 1)}\]
Für \(a = -4\) ist der Graph von \(G_{k_1}\) an der \(y\)-Achse gespiegelt.
Spiegeln von Funktionsgraphen
Spiegelung an der \(x\)-Achse: \(g(x) = -f(x)\)
Spiegelung an der \(y\)-Achse: \(h(x) = f(-x)\)
\[\Longrightarrow \quad k_2(x) = -4 \cdot \frac{x}{(x^2 + 1)}\]
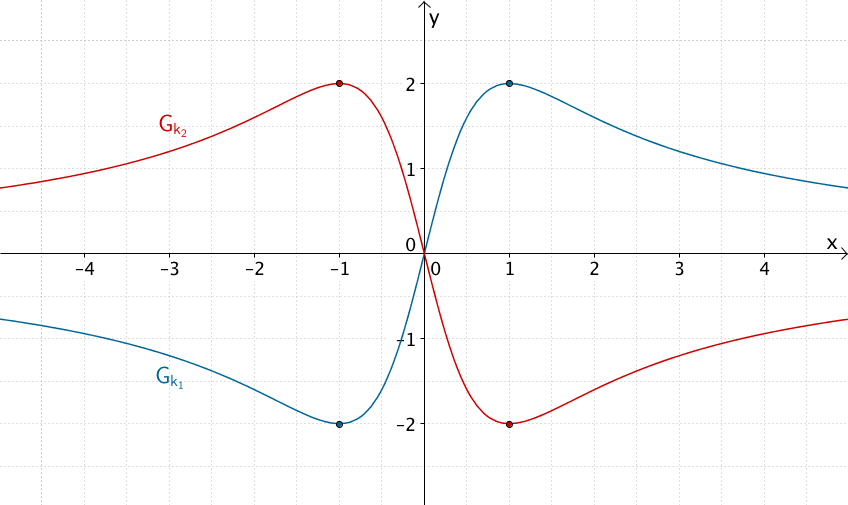
Graphen der in \(\mathbb R\) definierten gebrochenrationalen Funktionen \(k_1\) und \(k_2\) mit der Wertemenge \(\mathbb W = [-2;2]\)

