Berechnen Sie die mittlere Änderungsrate \(m_S\) von \(f\) im Intervall \([-0{,}5; 0{,}5]\) sowie die lokale Änderungsrate \(m_T\) an der Stelle \(x = 0\). Berechnen Sie, um wie viel Prozent \(m_S\) von \(m_T\) abweicht.
(4 BE)
Lösung zu Teilaufgabe 1c
\[f(x) = 2x \cdot e^{-0{,}5x^2}\,; \quad D = \mathbb R\]
Mittlere Änderungsrate \(m_S\)
![Mittlere Änderungsrate von f im Intervall [-0,5;0,5] Mittlere Änderungsrate von f im Intervall [-0,5;0,5]](/images/stories/B2013_A_I/B2013_A_I_T2_1c_01.png)
Die mittlere Änderungsrate \(m_S\) der Funktion \(f\) im Intervall \([-0{,}5;0{,}5]\) ist gleich der Steigung der Sekante \(S\), welche die Punkte \((-0{,}5)|f(-0{,}5)\) und \((0{,}5|f(0{,}5))\) festlegen.
Differenzenquotient oder mittlere Änderungsrate
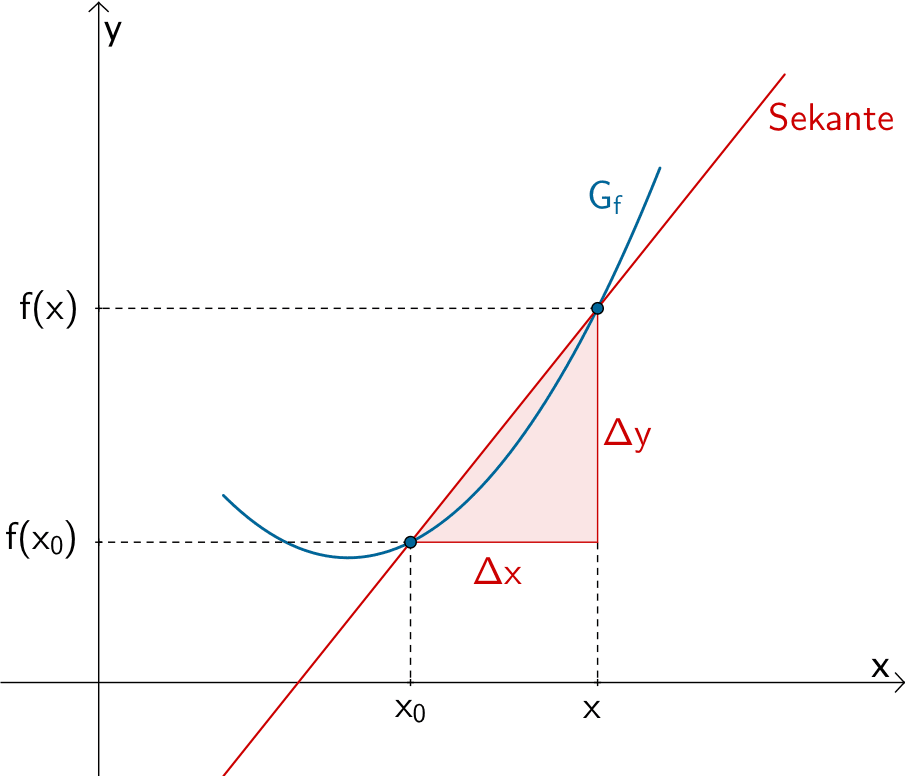
Der Differenzenquotient oder die mittlere Änderungsrate \(m_{s} = \dfrac{f(x) - f(x_{0})}{x - x_{0}}\) beschreibt die Steigung der Sekante durch den Punkt \((x_{0}|f(x_{0}))\) und einen weiteren Punkt des Graphen der Funktion \(f\).
\[\begin{align*} m_S &= \frac{f(0{,}5) - f(-0{,}5)}{0{,}5 - (-0{,}5)} \\[0.8em] &= \frac{2 \cdot 0{,}5 \cdot e^{-0{,}5 \cdot 0{,}5^2} - 2 \cdot (-0{,}5) \cdot e^{-0{,}5 \cdot (-0{,}5)^2}}{1} \\[0.8em] &= e^{-0{,}125} + e^{-0{,}125} \\[0.8em] &= 2e^{-0{,}125} \\[0.8em] &\approx 1{,}765 \end{align*}\]
Lokale Änderungsrate \(m_T\)
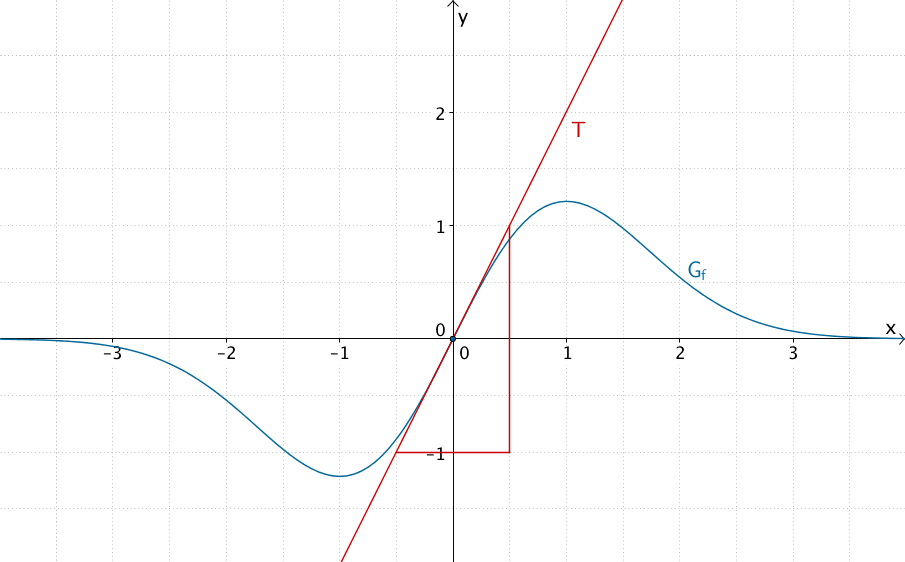
Die lokalen Änderungsrate \(m_T\) ist gleich der Steigung der Tangente \(T\) an den Graphen der Funktion \(f\) an der Stelle \(x = 0\).
Differentialquotient oder lokale bzw. momentane Änderungsrate
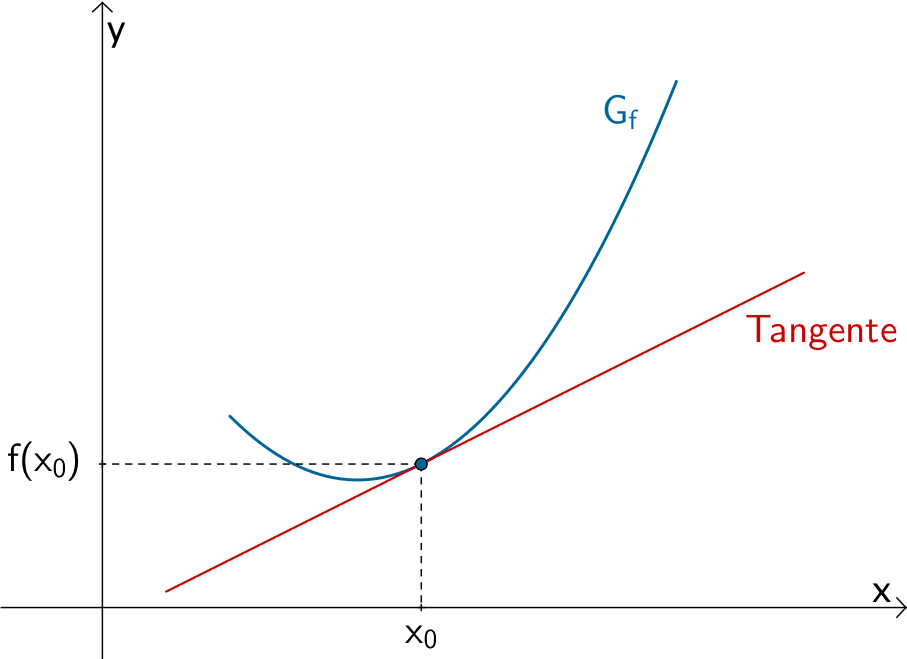
Der Differentialquotient oder die lokale bzw. momentane Änderungsrate \(m_{x_{0}} = \lim \limits_{x \, \to \, x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\) beschreibt den Grenzwert des Differenzenquotienten \(\dfrac{f(x) - f(x_{0})}{x - x_{0}}\) bei beliebig genauer Annäherung \(x \to x_{0}\) und damit die Steigung der Tangente an den Graphen der Funktion \(f\) an der Stelle \(x_{0}\).
Man nennt den Grenzwert \(m_{x_{0}}\) die Ableitung von \(f\) an der Stelle \(x_{0}\) und schreibt dafür \(f'(x_{0})\). Voraussetzung: Der Grenzwert existiert an der Stelle \(x_{0}\) und ist endlich.
\[f'(x_{0}) = \lim \limits_{x \, \to \, x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\]
(vgl. Merkhilfe)
\[m_T = \lim \limits_{x \, \to \, 0} \frac{f(x) - f(0)}{x - 0} = f'(0)\]
Die lokale Änderungsrate \(m_T\) ist gleich dem Wert der Ableitung der in \(\mathbb R\) differenzierteren Funktion \(f\) an der Stelle \(x = 0\).
\(\displaystyle f'(x) = 2e^{-0{,}5x^2} \cdot (1 - x^2)\) (siehe Teilaufgabe 1b)
\[m_T = f'(0) = 2 \cdot e^{-0{,}5 \cdot 0^2} \cdot (1 - 0^2) = 2 \cdot e^0 = 2\]
Prozentuale Abweichung von \(m_S\)
\[\frac{m_T - m_S}{m_T} = \frac{2 - 1{,}765}{2} \approx 0{,}118 = 11{,}8\,\%\]
Die mittlere Änderungsrate \(m_S\) weicht um 11,8 % von der lokalen Änderungsrate \(m_T\) ab.

