Teilaufgabe 3c
Lösung zu Teilaufgabe 3c
\[g_{1{,}4}(x) = 2x \cdot e^{-0{,}5x^2} + 1{,}4\,; \quad x \geq 0\]
Jahr, in dem die Geburtenziffer am stärksten abnimmt
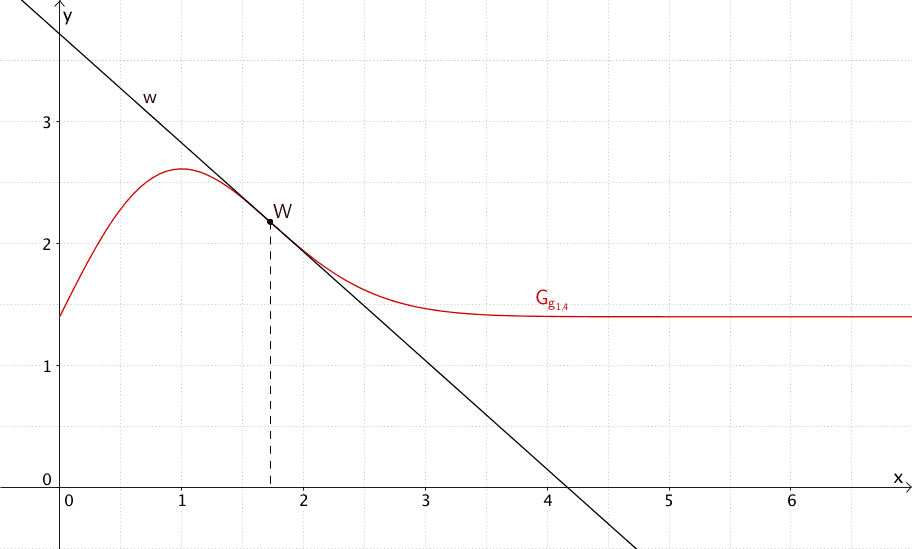
Graph der Funktion \(g_{1{,}4}\) für \(x \geq 0\) mit Wendepunkt \(W\) und Wendetangente \(w\)
Im Intervall \([0;+\infty]\) hat der Graph von \(g_{1{,}4}\) für \(x \approx 1{,}7\) eine Wendestelle an der die momentane Änderungsrate der Geburtenziffer maximal ist. Da \(G_{g_{1{,}4}}\) im Intervall \([1;+\infty]\) zudem strreng monoton fällt, nimmt die Geburtenziffer an der Wendestelle am stärksten ab.
\(x \approx 1{,}7\) entspricht dem Jahr 1972.
Im Jahr 1972 nimmt die Geburtenziffer am stärksten ab.
Beschreibung eines rechnerischen Nachweises dafür, dass die Geburtenziffer ab dem Jahr 1972 kontinuierlich schwächer wird
Vorgehensweise:
1. Nachweis der Wendestelle \(x_W\) von \(G_{g_{1{,}4}}\)
2. Nachweis, dass der Graph von \(g_{1{,}4}\) für \(x > x_W\) linksgekrümmt ist.
\(g''_{1{,}4}(x) > 0\) für \(x > x_W\)
3. Nachweis, dass die Funktion \(g_{1{,}4}\) für \(x \to \infty\) einen unteren Grenzwert besitzt.
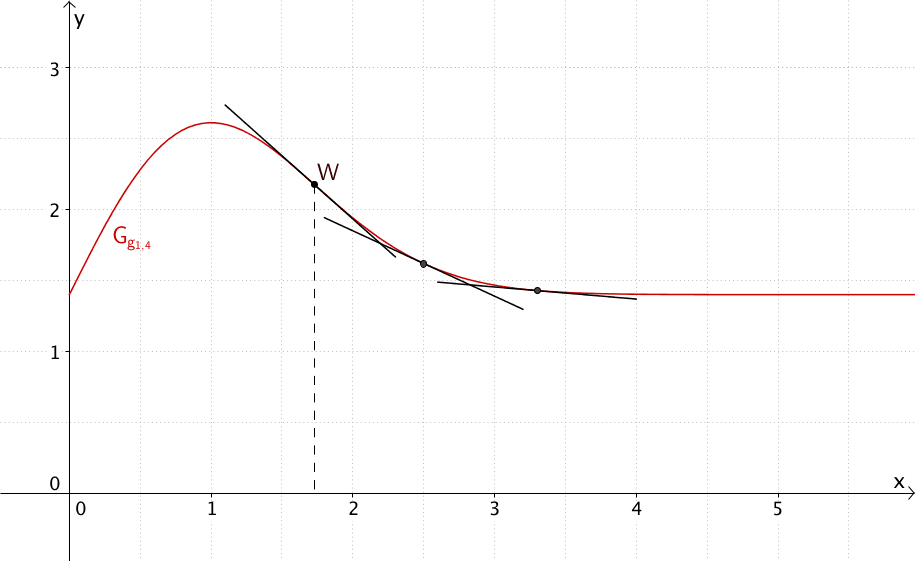
Da der Graph von \(g_{1{,}4}\) für \(x > x_W\) linksgekrümmt ist, nimmt die Steigung einer Tangente an einer Stelle \(x > x_W\) an \(G_{g_{1{,}4}}\) dem Betrag nach ab. Die Tangentensteigung beschreibt die momentane Änderungsrate der Geburtenziffer, also die Abnahme der Geburtenziffer zum Zeitpunkt \(x > x_W\). Somit wird die Abnahme der Geburtenziffer ab dem Zeitpunkt \(x_W\) kontinuierlich schwächer. Der Nachweis des unteren Grenzwerts von \(g_{1{,}4}\) stellt sicher, dass die Geburtenziffer nicht wieder zunimmt, sondern stetig abnimmt.
Ergänzung (nicht Teil der Prüfung!): Rechnerischer Nachweis
Die nachfolgende Ergänzung ist nicht Teil der Prüfung! Sie soll dem besseren Verständnis bzw. der Vertiefung des Themas dienen.
\[g_{1{,}4}(x) = 2x \cdot e^{-0{,}5x^2} + 1{,}4\,; \quad x \geq 0\]
1. Nachweis der Wendestelle \(x_W\) von \(G_{g_{1{,}4}}\)
Zweite Ableitung \(g''_{1{,}4}(x)\) bilden:
\[\begin{align*} g'_{1{,}4}(x) &= 2 \cdot e^{-0{,}5x^2} + 2x \cdot e^{-0{,}5x^2} \cdot (-0{,}5) \cdot 2x \\[0.8em] &= 2 \cdot e^{-0{,}5x^2} - 2x^2 \cdot e^{-0{,}5x^2} \\[0.8em] &= 2e^{-0{,}5x^2} \cdot (1 - x^2) \end{align*}\]
\[\begin{align*} g''_{1{,}4}(x) &= 2e^{-0{,}5x^2} \cdot (-0{,}5) \cdot 2x \cdot (1 - x^2) + 2e^{-0{,}5x^2} \cdot (-2x) \\[0.8em] &= -2x \cdot e^{-0{,}5x^2} \cdot (1 - x^2) - 4x \cdot e^{-0{,}5x^2} \\[0.8em] &= 2x \cdot e^{-0{,}5x^2} \cdot (x^2 - 3) \end{align*}\]
\[g''_{1{,}4}(x) \overset{!}{=} 0 \quad \Longrightarrow \quad (x = 0) \enspace \vee \enspace x^2 - 3 = 0\]
\[\begin{align*} x^2 - 3 &= 0 & &| + 3 \\[0.8em] x^2 &= 3 & &| \; \sqrt{\quad}\,, \enspace x \geq 0 \\[0.8em] x &= \sqrt{3} \\[0.8em] x &\approx 1{,}73 \end{align*}\]
Vorzeichenwechsel von \(g''_{1{,}4}(x)\) an der Stelle \(x = \sqrt{3}\):
\[g''_{1{,}4}(x) = 2x \cdot e^{-0{,}5x^2} \cdot (x^2 - 3)\]
In der Nähe der Stelle \(x = \sqrt{3}\) gilt für \(x < \sqrt{3}\) und für \(x > \sqrt{3}\):
\[2x \cdot e^{-0{,}5x^2} > 0\]
Somit bestimmt der Falktor \((x^2 - 3)\) den Vorzeichenwechsel von \(g''_{1{,}4}(x)\) an der Stelle \(x = \sqrt{3}\).
Für \(x < \sqrt{3} \quad \Longrightarrow \quad x^2 - 3 < 0 \quad \Longrightarrow \quad g''_{1{,}4}(x) < 0\)
Für \(x > \sqrt{3} \quad \Longrightarrow \quad x^2 - 3 > 0 \quad \Longrightarrow \quad g''_{1{,}4}(x) > 0\)
\(\Longrightarrow \quad x_W = \sqrt{3}\) ist Wendestelle von \(G_{g_{1{,}4}}\).
\(x_W = \sqrt{3} \approx 1{,}73\) entspricht dem Jahr 1972.
2. Nachweis, dass der Graph von \(g_{1{,}4}\) für \(x > x_W\) linksgekrümmt ist.
\[x_W = \sqrt{3}\]
\(g''_{1{,}4}(x) > 0\) für \(x > \sqrt{3} \quad \Longrightarrow \quad G_{g_{1{,}4}}\) ist linksgekrümmt.
3. Nachweis, dass die Funktion \(g_{1{,}4}\) für \(x \to \infty\) einen unteren Grenzwert besitzt.
Verhalten von \(g_{1{,}4}(x)\) für \(x \to + \infty\):
\[\begin{align*} \lim \limits_{x \, \to \, + \infty} g_{1{,}4}(x) &= \lim \limits_{x \, \to \, + \infty} 2x \cdot e^{-0{,}5x^2} + 1{,}4 \\[0.8em] &= \lim \limits_{x \, \to \, + \infty} \; \frac{2x}{e^{0{,}5x^2}} + 1{,}4 \\[0.8em] &= 1{,}4 \end{align*}\]
Für \(x \to + \infty\) wächst \(e^{0{,}5x^2}\) schneller als \(x\).
Fazit:
Ab dem Jahr 1972 wird die Abnahme der Geburtenziffer kontinuierlich schwächer und nähert sich dem unteren Grenzwert 1,4.
