Mathematik Abitur Bayern 2013 Analysis II - Aufgaben mit Lösungen

Geben Sie für die Funktion \(f\) mit \(f(x) = \ln (2013 - x)\) den maximalen Definitionsbereich \(D\), das Verhalten von \(f\) an den Grenzen von \(D\) sowie die Schnittpunkte des Graphen von \(f\) mit den Koordinatenachsen an.

(5 BE)

Der Graph der in \(\mathbb R\) definierten Funktion \(f \colon x \mapsto x \cdot \sin x\) verläuft durch den Koordinatenursprung. Berechnen Sie \(f''(0)\) und geben Sie das Krümmungsverhalten des Graphen von \(f\) in unmittelbarer Nähe des Koordinatenursprungs an.

(4 BE)

Gegeben sind die in \(\mathbb R\) definierten Funktionen \(g \colon x \mapsto e^{-x}\) und \(h \colon x \mapsto x^3\).

Veranschaulichen Sie durch eine Skizze, dass die Graphen von \(g\) und \(h\) genau einen Schnittpunkt haben.

(2 BE)

Bestimmen Sie einen Näherungswert \(x_1\) für die \(x\)-Koordinate dieses Schnittpunkts, indem Sie für die in \(\mathbb R\) definierte Funktion \(d \colon x \mapsto g(x) - h(x)\) den ersten Schritt des Newton-Verfahrens mit dem Startwert \(x_0 = 1\) durchführen.

(4 BE)

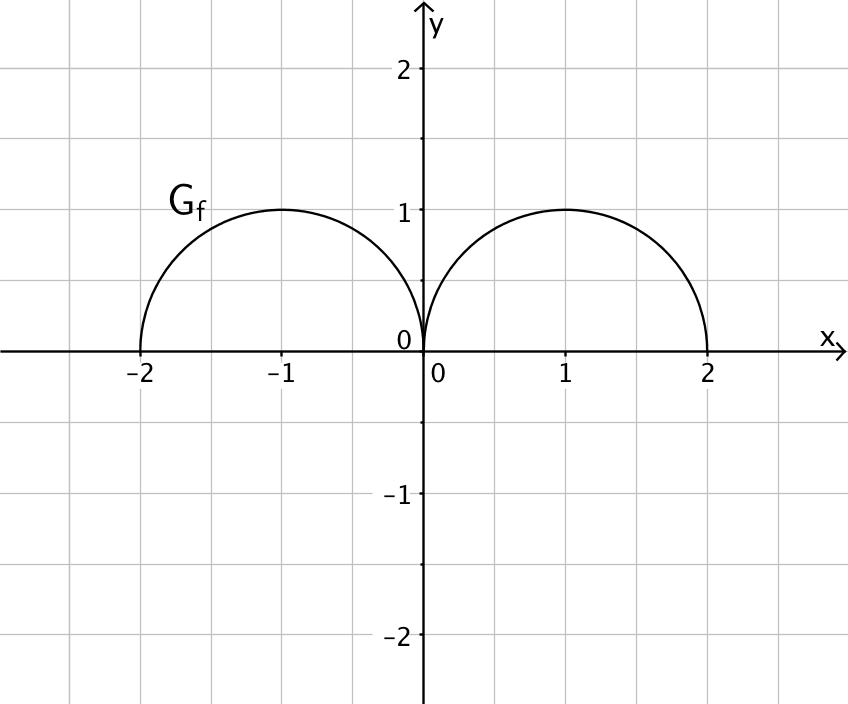Abb. 1

Abbildung 1 zeigt den Graphen \(G_f\) der Funktion \(f\) mit Definitionsbereich \([-2;2]\). Der Graph besteht aus zwei Halbkreisen, die die Mittelpunkte \((-1|0)\) bzw. \((1|0)\) sowie jeweils den Radius 1 besitzen. Betrachtet wird die in \([-2;2]\) definierte Integralfunktion \(\displaystyle F \colon \mapsto \int_0^x f(t)\,dt\).

Geben Sie \(F(0)\), \(F(2)\) und \(F(-2)\) an.

(3 BE)

Skizzieren Sie den Graphen von \(F\) in Abbildung 1.

(2 BE)

Gegeben ist die Funktion \(\displaystyle f \colon x \mapsto \frac{1}{2}x - \frac{1}{2} + \frac{8}{x + 1}\) mit Definitionsbereich \(\mathbb R \backslash \{-1\} \).

Abbildung 2 zeigt den Graphen \(G_f\) von \(f\).

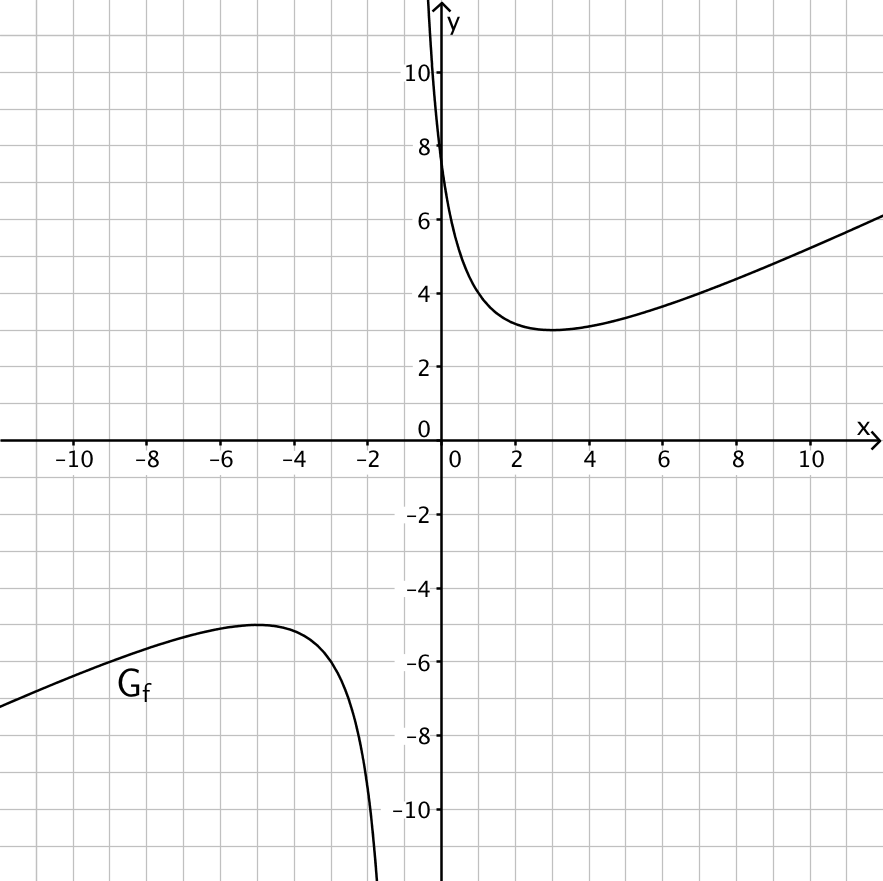Abb. 2

Geben Sie die Gleichungen der Asymptoten von \(G_f\) an und zeigen Sie rechnerisch, dass \(G_f\) seine schräge Asymptote nicht schneidet. Zeichnen Sie die Asymptoten in Abbildung 2 ein.

(6 BE)

Bestimmen Sie rechnerisch Lage und Art der Extrempunkte von \(G_f\,\).

(8 BE)

Abbildung 2 legt die Vermutung nahe, dass \(G_f\) bezüglich des Schnittpunkts \(P\,(-1|-1)\) seiner Asymptoten symmetrisch ist. Zum Nachweis dieser Symmetrie von \(G_f\) kann die Funktion \(g\) betrachtet werden, deren Graph aus \(G_f\) durch Verschiebung um 1 in positive \(x\)-Richtung und um 1 in positive \(y\)-Richtung hervorgeht.

Bestimmen Sie einen Funktionsterm von \(g\). Weisen Sie anschließend die Punktsymmetrie von \(G_f\) nach, indem Sie zeigen, dass der Graph von \(g\) punktsymmetrisch bezüglich des Koordinatenursprungs ist.

(Teilergebnis: \(\displaystyle g(x) = \frac{1}{2}x + \frac{8}{x}\))

(6 BE)

Zeigen Sie, dass \(\displaystyle \int_0^4 f(x)\,dx = 2 + 8 \cdot \ln 5\) gilt.

Bestimmen Sie nun ohne weitere Integration den Wert des Integrals \(\displaystyle \int_{-6}^{-2} f(x)\,dx\); veranschaulichen Sie Ihr Vorgehen durch geeignete Eintragungen in Abbildung 2.

(8 BE)

Eine vertikal stehende Getränkedose hat die Form eines geraden Zylinders. Die Lage des gemeinsamen Schwerpunkts \(S\) von Dose und enthaltener Flüssigkeit hängt von der Füllhöhe der Flüssigkeit über dem Dosenboden ab. Ist die Dose vollständig gefüllt, so beträgt die Füllhöhe 15 cm.

Die bisher betrachtete Funktion \(f\) gibt für \(0 \leq x \leq 15\) die Höhe von \(S\) über dem Dosenboden in Zentimetern an; dabei ist \(x\) die Füllhöhe in Zentimetern (vgl. Abbildung 3).

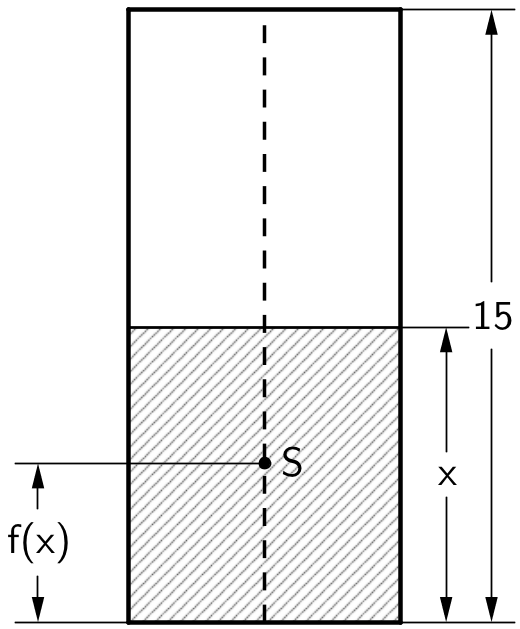
Abb. 3

Berechnen Sie \(f(0)\) und \(f(15)\). Interpretieren Sie die beiden Ergebnisse im Sachzusammenhang.

(3 BE)

Die zunächst leere Dose wird langsam mit Flüssigkeit gefüllt, bis die maximale Füllhöhe von 15 cm erreicht ist. Beschreiben Sie mithilfe von Abbildung 2 die Bewegung des Schwerpunkts \(S\) während des Füllvorgangs. Welche Bedeutung im Sachzusammenhang hat die Tatsache, dass \(x\)-Koordinate und \(y\)-Koordinate des Tiefpunkts von \(G_f\) übereinstimmen?

(3 BE)

Für welche Füllhöhen \(x\) liegt der Schwerpunkt \(S\) höchstens 5 cm hoch? Beantworten Sie diese Frage zunächst näherungsweise mithilfe von Abbildung 2 und anschließend durch Rechnung.

(6 BE)