Gegeben ist die Funktion \(\displaystyle f \colon x \mapsto \frac{1}{2}x - \frac{1}{2} + \frac{8}{x + 1}\) mit Definitionsbereich \(\mathbb R \backslash \{-1\} \).
Abbildung 2 zeigt den Graphen \(G_f\) von \(f\).
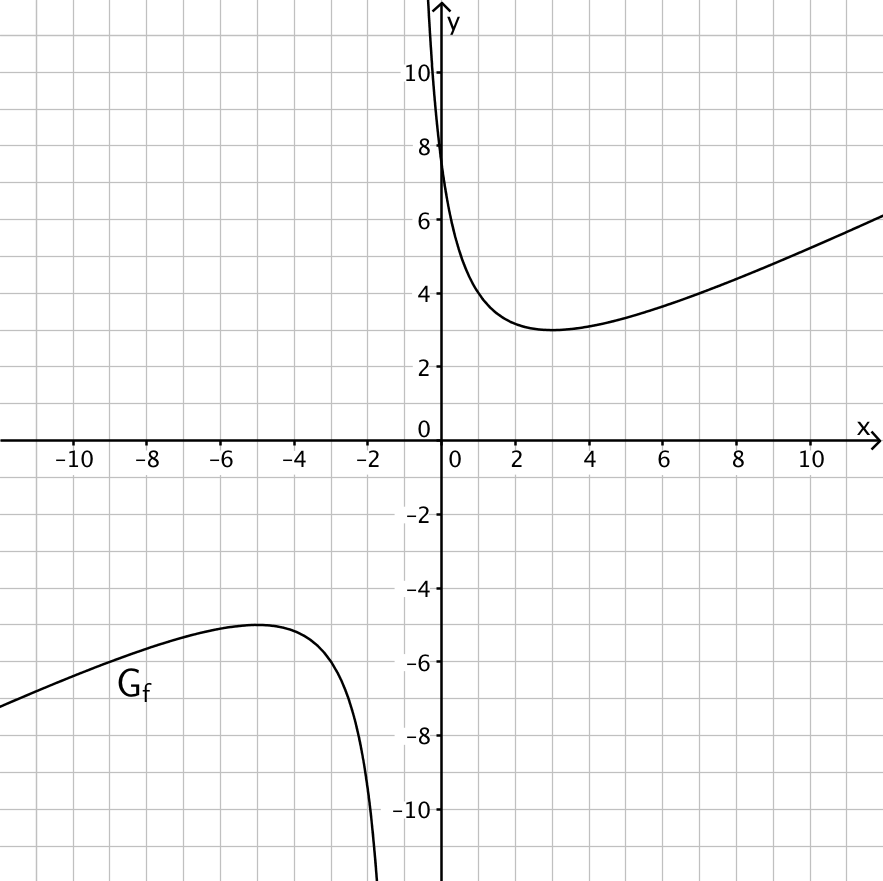 Abb. 2
Abb. 2
Geben Sie die Gleichungen der Asymptoten von \(G_f\) an und zeigen Sie rechnerisch, dass \(G_f\) seine schräge Asymptote nicht schneidet. Zeichnen Sie die Asymptoten in Abbildung 2 ein.
(6 BE)
Lösung zu Teilaufgabe 1a
\[f(x) = \frac{1}{2}x - \frac{1}{2} + \frac{8}{x + 1}\,; \quad D = \mathbb R \, \backslash \, \{-1\}\]
Gleichungen der Asymptoten von \(G_f\)
Die gebrochenrationale Funktion \(f\) besitzt für \(x = -1\) (Nullstelle des Nenners) eine Polstelle mit Vorzeichenwechsel.
\(\Longrightarrow \quad\) senkrechte Asymptote mit der Gleichung \(x = -1\)
Die schräge Asymptote von \(G_f\) beschreibt das Verhalten von \(f\) für \(x \to \pm \infty\):
\[\begin{align*}\lim \limits_{x \, \to \, \pm \infty} f(x) &= \lim \limits_{x \, \to \, \pm \infty} \biggl( \frac{1}{2}x - \frac{1}{2} + \underbrace{\frac{8}{x + 1}}_{\to \, 0} \biggr) \\[0.8em] &= \lim \limits_{x \, \to \, \pm \infty} \biggl( \frac{1}{2}x - \frac{1}{2} \biggr)\end{align*}\]
\(\Longrightarrow \quad\) schräge Asymptote mit der Gleichung \(\displaystyle y = \frac{1}{2}x - \frac{1}{2}\)
Nachweis, dass \(G_f\) seine schräge Asymptote nicht schneidet
Zur Berechnung der Schnittpunkte zweier Funktionsgraphen werden die Funktionsterme gleichgesetzt.
\[\begin{align*}\frac{1}{2}x - \frac{1}{2} + \frac{8}{x + 1} &= \frac{1}{2}x - \frac{1}{2} & &| - \frac{1}{2}x + \frac{1}{2} \\[0.8em] \frac{8}{x + 1} &= 0 \end{align*}\]
Keine Lösung, da \(8 \neq 0\)
\(\Longrightarrow \quad G_f\) schneidet seine schräge Asymptote nicht.
Einzeichnen der Asymptoten
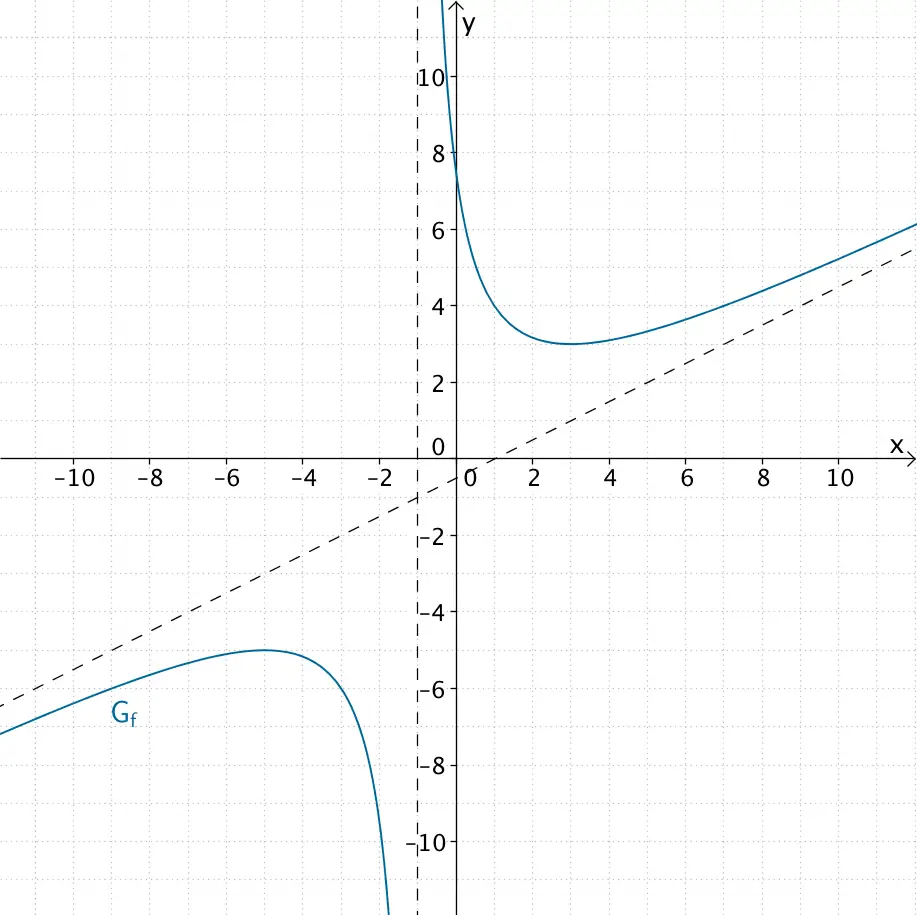
Graph der gebrochenrationalen Funktion \(f\), senkrechte Asymptote \(x = -1\) und schräge Asymptote \(\displaystyle y = \frac{1}{2}x - \frac{1}{2}\)


