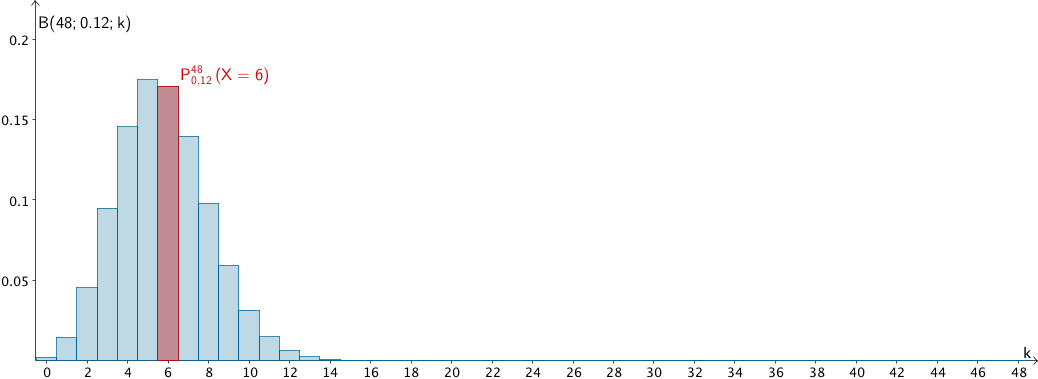Der Kandidat der Partei A spricht an einem Tag während seines Wahlkampfs 48 zufällig ausgewählte Wahlberechtigte an. Bestimmen Sie die Wahrscheinlichkeit dafür, dass sich darunter genau sechs Jungwähler befinden.
(3 BE)
Lösung zu Teilaufgabe 1c
Binomialverteilung
Binomialverteilte Zufallsgröße
Für eine Zufallsgröße \(X\), welche bei einer Bernoulli-Kette der Länge \(n\) die Anzahl der Treffer \(k \in \{0,1,\dots,n\}\) mit der Trefferwahrscheinlichkeit \(p\) angibt, gilt:
Binomialverteilung (vgl. Merkhilfe)
\[P_{p}^{n}(X = k) = B(n;p;k) = \binom{n}{k} \cdot p^{k} \cdot (1 - p)^{n - k} \quad (0 \leq k \leq n)\]
Eine Binomialverteilung ist durch die Parameter \(n\) und \(p\) eindeutig bestimmt und wird durch das Symbol \(B(n:p)\) gekennzeichnet. \(X\) heißt binomialverteilt nach \(B(n;p)\).
Voraussetzung für eine Binomialverteilung
Ein Zufallsexperiment, bei dem nur zwei sich gegenseitig ausschließende Ereignisse \(A\) und \(\overline{A}\) mit konstanten Wahrscheinlichkeiten eintreten können (Bernoulli-Experiment).
Zufallsgröße \(X\colon\enspace\)Anzahl der Jungwähler unter den zufällig ausgewählten Wahlberechtigten
Analyse der Angabe:
„...spricht...48 zufällig ausgewählte Wahlberechtigte an."
\(\Longrightarrow \quad n = 48\)
„Bestimmen Sie die Wahrscheinlichkeit dafür, dass sich darunter genau sechs Jungwähler befinden."
\(\Longrightarrow \quad X = 6\)
\(\Longrightarrow \quad p = P(J) = 0{,}12\) (siehe Teilaufgabe 1a)
Die Zufallsgröße \(X\) ist nach \(B(48; 0{,}12)\) binomialverteilt.
Das Stochastische Tafelwerk mit Abiturzulassung beinhaltet keine Binomialverteilung für eine Trefferwahrscheinlichkeit \(p = 0{,}12\) bzw. für eine Bernoullikette mit der Länge \(n = 48\). Die Wahrscheinlichkeit \(P_{0{,}12}^{48}(X = 6)\) muss errechnet werden.
Anwenden der Formel von Bernoulli:
Formel von Bernoulli
Wahrscheinlichkeit für genau \(k\) Treffer bei einer Bernoullikette der Länge \(n\) und der Trefferwahrscheinlichkeit \(p\) für das Eintreten eines betrachteten Ereignisses:
\[P(X = k) = B(n;p;k) = \binom{n}{k} \cdot p^k \cdot (1 - p)^{n - k}\]
\[k \in \{0,1,\dots,n\}\]
\[\begin{align*} P_{0{,}12}^{48}(X = 6) &= B(48; 0{,}12; 6) \\[0.8em] &= \binom{48}{6} \cdot 0{,}12^6 \cdot (1 - 0{,}12)^{48 - 6} \\[0.8em] &= \binom{48}{6} \cdot 0{,}12^6 \cdot 0{,}88^{42} \\[0.8em] &\approx 0{,}171 = 17{,}1\,\% \end{align*}\]
Wahrscheinlichkeitsverteilung der nach \(B(48; 0{,}12)\) binomialverteilten Zufallsgröße \(X\), WAhrscheinlichkeit \(P_{0{,}12}^{48}(X = 6) = B(48; 0{,}12; 6)\)