Der Umfrage zufolge hätte der Kandidat der Partei A etwa 50 % aller Stimmen erhalten, wenn die Wahl zum Zeitpunkt der Befragung stattgefunden hätte. Ein Erfolg im ersten Wahlgang, für den mehr als 50 % aller Stimmen erforderlich sind, ist demnach fraglich. Deshalb rät die von der Partei A eingesetzte Wahlkampfberaterin in der Endphase des Wahlkampfs zu einer zusätzlichen Kampagne. Der Schatzmeister der Partei A möchte die hohen Kosten, die mit einer zusätzlichen Kampagne verbunden wären, jedoch möglichst vermeiden.
Um zu einer Entscheidung über die Durchführung einer zusätzlichen Kampagne zu gelangen, soll die Nullhypothese „Der Kandidat der Partei A würde gegenwärtig höchstens 50 % aller Stimmen erhalten." mithilfe einer Stichprobe von 200 Wahlberechtigten auf einem Signifikanzniveau von 5 % getestet werden. Bestimmen Sie die zugehörige Entscheidungsregel.
(5 BE)
Lösung zu Teilaufgabe 2a
Signifikanztest
Zufallsgröße \(Z\colon\enspace\)Anzahl der Befragten, die den Kandidaten der Partei A wählen
Analyse der Angabe:
„... soll die Nullhypothese ... höchstens 50 % aller Stimmen ..."
\(\Longrightarrow \quad H_0\,\colon\; p \leq 0{,}5\)
„... mithilfe einer Stichprobe von 200 Wahlberechtigten ..."
\(\Longrightarrow \quad\) Stichprobenumfang \(n = 200\)
„... auf einem Signifikanzniveau von 5 % getestet weden."
\(\Longrightarrow \quad\) Signifikanzniveau \(\alpha = 0{,}05\)
Mit der Wahl der Nullhypothese \(H_0\,\colon\; p \leq 0{,}5\) soll die Irrtumswahrscheinlichkeit dafür, dass eine Zusatzkampagne abgelehnt wird, obwohl der Kandidat der Partei A tasächlich höchstens 50 % aller Stimmen erhalten würde, eingeschränkt werden (siehe auch Teilaufgabe 2b).
\(\Longrightarrow \quad P(\text{„Fehler 1. Art"}) \leq 0{,}05\)
Rechsseitiger Signifikanztest
Einseitiger Signifikanztest zum Signifikanzniveau \(\boldsymbol{\alpha}\)
Ein einseitiger Signifikanztest zum Signifikanzniveau \(\alpha\) überprüft eine Vermutung, dass eine Wahrscheinlichkeit \(p\) größer bzw. kleiner als eine bestimmte Wahrscheinlichkeit \(p_{0}\) ist. Dabei darf die Wahrscheinlichkeit für den Fehler 1. Art höchstens den Wert des Signifikanzniveaus \(\alpha\) erreichen.
Linksseitiger Signifikanztest
\[H_0 \colon p_0 \geq p \quad H_1 \colon p_1 < p\]
Ablehnungsbereich von \(H_0\):
\[\overline{A} = \{0; 1; ...; k\}\]
Bedingung für den Fehler 1. Art:
\[\begin{align*} P_{p_{0}}^{n}(\text{„Fehler 1. Art"}) &\leq \alpha \\[0.8em] P_{p_{0}}^{n}(X \in \overline{A}) &\leq \alpha \\[0.8em] P_{p_{0}}^{n}(X \leq k) &\leq \alpha \\[1.6em] \overset{\text{ST}}{\Longrightarrow} \enspace k \enspace \Longrightarrow \enspace A, \overline{A} \end{align*}\]
Rechtsseitiger Signifikanztest
\[H_0 \colon p_0 \leq p \quad H_1 \colon p_1 > p\]
Ablehnungsbereich von \(H_0\):
\[\overline{A} = \{k + 1; ...; n\}\]
Bedingung für den Fehler 1. Art:
\[\begin{align*} P_{p_{0}}^{n}(\text{„Fehler 1. Art"}) &\leq \alpha \\[0.8em] P_{p_{0}}^{n}(X \in \overline{A}) &\leq \alpha \\[0.8em] P_{p_{0}}^{n}(X \geq k +1) &\leq \alpha \\[0.8em] 1 - P_{p_{0}}^{n}(X \leq k) &\leq \alpha & &| - 1 \\[0.8em] - P_{p_{0}}^{n}(X \leq k) &\leq \alpha - 1 &&| \textcolor{red}{\cdot (-1)} \\[0.8em] P_{p_{0}}^{n}(X \leq k) &\textcolor{red}{\geq} 1 - \alpha \\[1.6em] \overset{\text{ST}}{\Longrightarrow} \enspace k \enspace \Longrightarrow \enspace A, \overline{A} \end{align*}\]
ST: Stochastisches Tafelwerk
Nullhypothese \(H_0\,\colon\; p \leq 0{,}5\)
Gegenhypothese \(H_1\,\colon\; p > 0{,}5\)
Annahmebereich von \(H_0\,\colon\; A = \{0; 1; \dots; k \}\)
Ablehnungsbereich von \(H_0\,\colon\; \overline{A} = \{k + 1; \dots; 200\}\)
Bedingung für den Fehler 1.Art formulieren:
\[P_{0{,}5}^{200}(Z \geq k + 1) \enspace \overset{!}{\leq} \enspace 0{,}05\]
Betrachten des Gegenereignisses:
Betrachten des Gegenereignisses (mindestens \(k\) Treffer)
Kumulative Wahrscheinlichkeiten der Form \(P(X \geq k)\) lassen sich im Stochastischen Tafelwerk (ST) nicht nachschlagen. Die Betrachtung des Gegenereignisses ermöglicht das Verwenden des Stochastischen Tafelwerks:
\[P(X \geq k) = 1 - P(X \leq k - 1)\]
Die Kumulative Verteilungsfunktion \(F_{p}^{n}(k) = P^n_p(X \leq k) = \sum \limits_{i\;=\;0}^{k} B(n;p;i)\) ist für bestimmte Werte der Parameter \(p\) und \(n\) in der rechten Spalte des Stochastischen Tafelwerks mit Abiturzulassung tabellarisiert.
\[\begin{align*} P_{0{,}5}^{200}(Z \geq k + 1) &\leq 0{,}05 \\[0.8em] 1 - P_{0{,}5}^{200}(Z \leq k) &\leq 0{,}05 & &| - 1 \\[0.8em] -P_{0{,}5}^{200}(Z \leq k) &\leq -0{,}95 & &| \cdot (-1) \quad \text{Relationszeichen dreht!} \\[0.8em] P_{0{,}5}^{200}(Z \leq k) &\geq 0{,}95 \end{align*}\]
Kumulative Verteilungsfunktion einer nach \(B(n, p)\) binomialverteilten Zufallsgröße \(X\)
\[F^n_p (k) = P^n_p (X \leq k) = \sum_{i \, = \, 0}^k B(n; p; i) = \sum_{i \, = \, 0}^k \binom{n}{i} \cdot p^i \cdot (1 - p)^{n - i}\]
Wobei \(n\) die Länge der Bernoullikette, \(p\) die Trefferwahrscheinlichkeit für das Eintreten des betrachteten Ereignisses und \(k \in \{0,1,\dots,n\}\) die Anzahl der Treffer ist.
Das Stochastische Tafelwerk (ST) listet die Werte der Kumulativen Verteilungsfunktion jeweils in der rechten Spalte einer betrachteten Tabelle der Parameter \(n\) und \(p\).
Stochastisches Tafelwerk (ST) verwenden:
\[P^{200}_{0{,}5} (Z \leq k) = F^{200}_{0{,}5} (k) = \sum \limits_{i \; = \; 0}^{k} B(200; 0{,}5; i) \enspace \overset{!}{\geq} \enspace 0{,}95\]
\[\overset{\text{ST}}{\Longrightarrow} \quad k = 112 \quad \left( F^{200}_{0{,}5} (112) \quad \overset{\text{ST}}{=} \quad 0{,}96158 \right)\]
Entscheidungsregel formulieren:
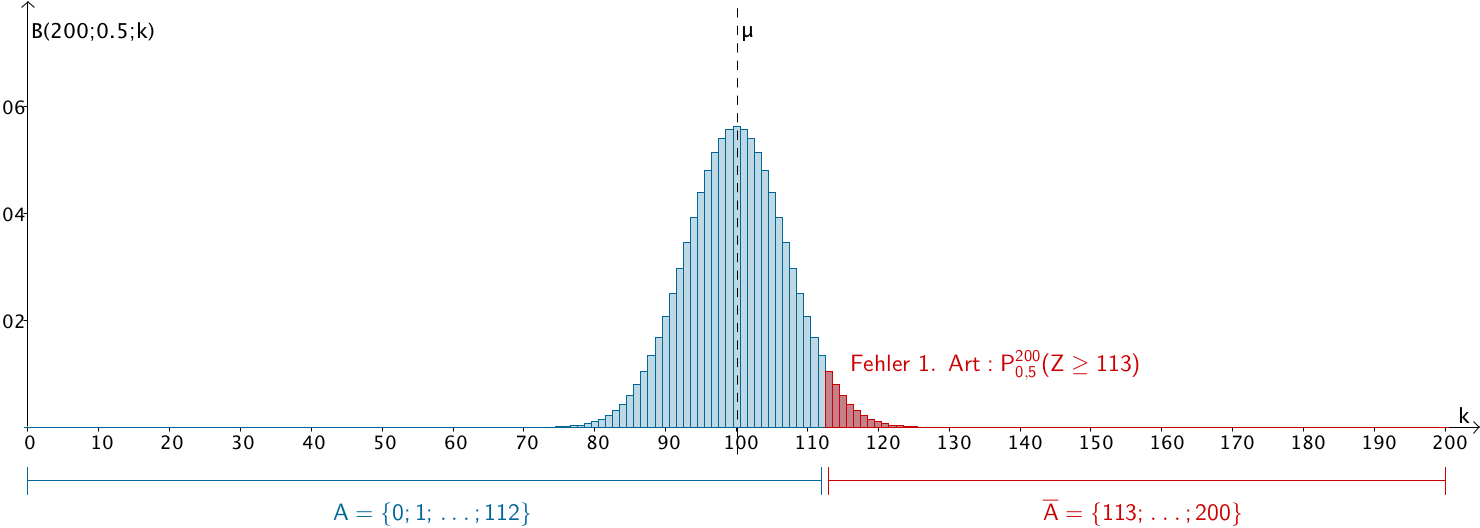
Annahmebereich von \(H_0\,\colon\; A = \{0; 1; \dots; 112 \}\)
Ablehnungsbereich von \(H_0\,\colon\; \overline{A} = \{113; \dots; 200\}\)
Wenn höchstens 112 der 200 Befragten für den Kandidaten der Partei A stimmen, wird die zusätzliche Kampagne durchgeführt.