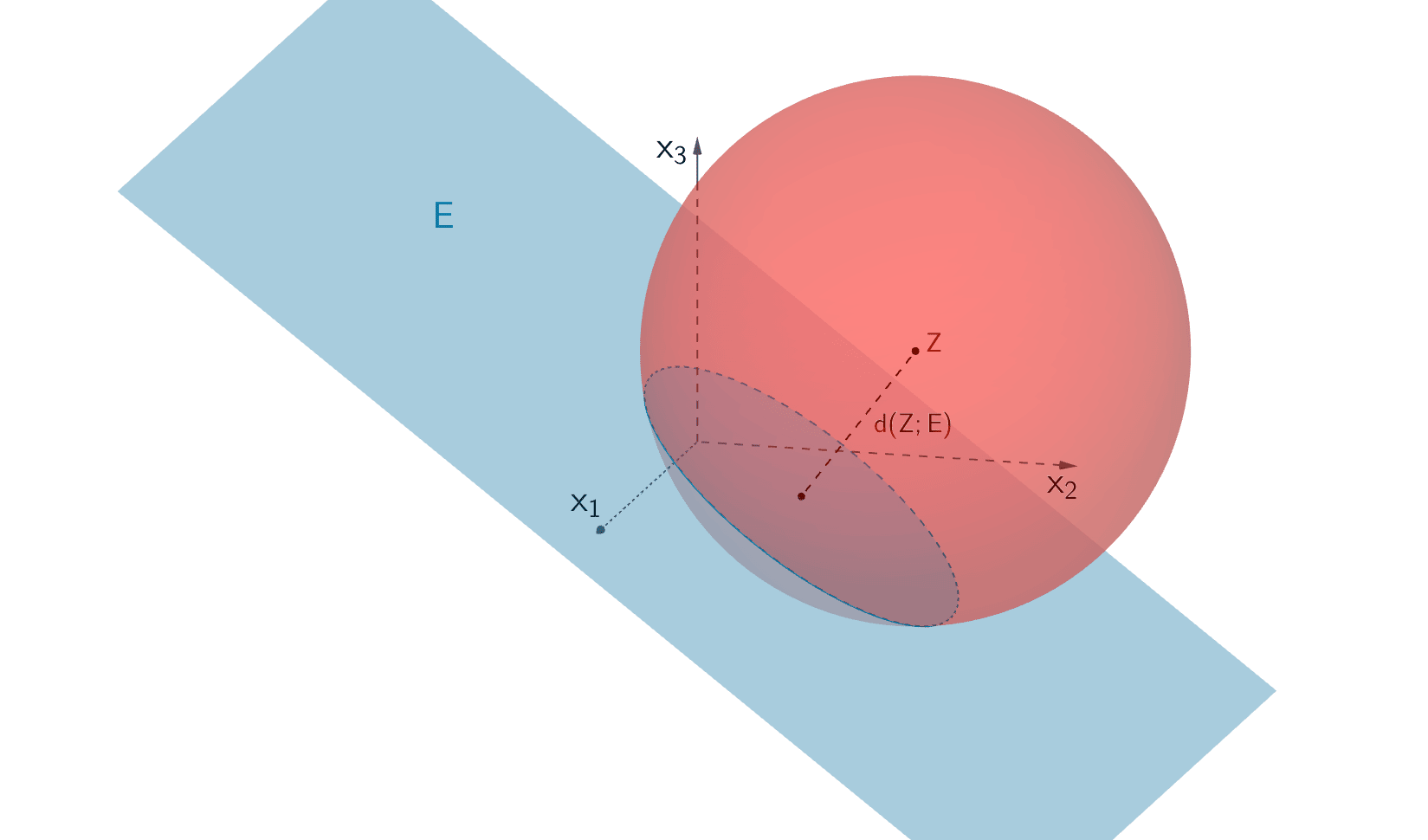
Untersuchen Sie rechnerisch, ob die Kugel mit Mittelpunkt \(Z\,(1|6|3)\) und Radius 7 die Ebene \(E\) schneidet.
(4 BE)
Lösung zu Teilaufgabe 2b
Die Kugel schneidet die Ebene \(E\), wenn der Abstand \(d\,(Z;E)\) des Kugelmittelpunkts \(Z\) von der Ebene \(E\) kleiner ist als der Radius der Kugel.
\[E\,\colon \, 3x_2 + 4x_3 = 5\]
\[Z\,(1|6|3)\,, \quad r = 7\]
Abstand eines Punktes von einer Ebene
Abstand eines Punktes von einer Ebene
Für den Abstand \(d(P;E)\) eines Punktes \(P(p_{1}|p_{2}|p_{3})\) zu einer in der Hesseschen Normalenform (HNF) vorliegenden Ebene \(E\) gilt:
Vektordarstellung
\[E \colon \overrightarrow{n}^{0}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0 \enspace (\text{HNF})\]
\[d(P;E) = \left| \overrightarrow{n}^{0}_{E} \circ (\overrightarrow{P} - \overrightarrow{A}) \right|\]
Koordinatendarstellung
\[E \colon \frac{n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0}}{\sqrt{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}} = 0 \enspace (\text{HNF})\]
\[d(P;E) = \left| \frac{n_{1}p_{1} + n_{2}p_{2} + n_{3}p_{3} + n_{0}}{\sqrt{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}} \right|\]
Dabei ist \(\overrightarrow{n}^{0}_{E} = \dfrac{\overrightarrow{n}_{E}}{\vert \overrightarrow{n}_{E} \vert}\) der Einheitsvektor des Normalenvektors \(\overrightarrow{n}_{E}\) der Ebene \(E\).
\[E\,\colon \, 3x_2 + 4x_3 = 5 \quad \Longrightarrow \quad n_{E} = \begin{pmatrix} 0 \\ 3 \\ 4 \end{pmatrix}\]
Betrag des Normalenvektors der Ebene \(E\):
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\vert \overrightarrow{n}_{E} \vert = \begin{pmatrix} 0 \\ 3 \\ 4 \end{pmatrix} = \sqrt{0^2 + 3^2 + 4^2} = \sqrt{25} = 5\]
\[E^{HNF} \colon \; \frac{3x_2 + 4x_3 - 5}{5} = 0\]
Abstand \(d\,(Z;E)\) berechnen:
\[Z\,(1|6|3)\]
\[\begin{align*} d\,(Z;E) &= \left| \frac{3z_2 + 4z_3 - 5}{5} \right| \\[0.8em] &= \left| \frac{3 \cdot 6 + 4 \cdot 3 - 5}{5} \right| \\[0.8em] &= \left| \frac{18 + 12 -5}{5} \right| \\[0.8em] &= \left| \frac{25}{5} \right| \\[0.8em] &= 5 \end{align*}\]
\[r= 7\]
\[\Longrightarrow \quad d\,(Z;E) < r\]
Die Kugel mit dem Mittelpunkt \(Z\,(1|6|3)\) und dem Radius 7 schneidet die Ebene \(E\).