Teilaufgabe 1b
Lösung zu Teilaufgabe 1b
\[f(x) = 2 - \sqrt{12 - 2x}\,; \quad D_{f} = \; ]-\infty;6]\]
Term der Ableitungsfunktion \(f'\) von \(f\)
\[f(x) = 2 - \sqrt{12 - 2x} = 2 - (12 - 2x)^{\frac{1}{2}}\]
\[\begin{align*} f'(x) &= 0 - \frac{1}{2} \cdot (12 - 2x)^{-\frac{1}{2}} \cdot (-2) \\[0.8em] &= (12 - 2x)^{-\frac{1}{2}} \\[0.8em] &= \frac{1}{\sqrt{12 - 2x}} \end{align*}\]
Maximale Definitionsmenge von \(f'\)
\[f'(x) = \frac{1}{\sqrt{12 - 2x}}\]
Der Nenner darf nicht Nulls sein und der Term unter der Wurzel (Radikant) darf nicht negativ sein.
\[\begin{align*} 12 - 2x &> 0 & &| + 2x \\[0.8em] 12 &> 2x & &| : 2 \\[0.8em] 6 &> x \end{align*}\]
\[D_{f'} = \; ]-\infty;6[\]
Verhalten von \(f'\) für \(x \to 6\)
\[\lim \limits_{x \, \to \, 6} f'(x) = \lim \limits_{x \, \to \, 6} \; \frac{1}{\underbrace{\sqrt{12 - 2x}}_{\to \, 0}} = \infty\]
Schlussfolgerung der Eigenschaft von \(G_f\) aus \(\lim \limits_{x \, \to \, 6} f'(x) = \infty\)
\[\lim \limits_{x \, \to \, 6} f'(x) = \lim \limits_{x \, \to \, 6} m_{t} = \infty\]
An der Stelle \(x = 6\) geht die Steigung der Tangente an \(G_f\) gegen Unendlich, d.h. die Tangente ist beliebig steil (senkrecht). Mit \(f(6) = 2\) und\(D_{f} = \; ]-\infty;6]\) (siehe Teilaufgabe 1a) folgt daraus, dass \(G_f\) an der Stelle \(x = 6\) senkrecht auf einer gedachten Geraden mit der Gleichung \(y = 2\) endet.
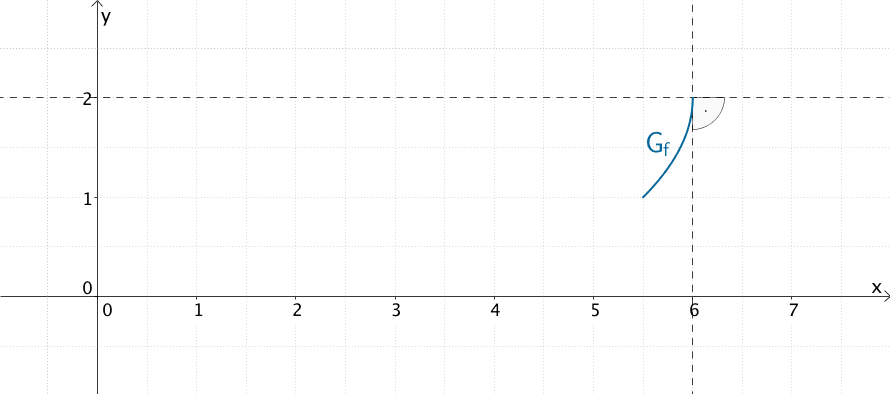
Verhalten des Graphen der Funktion \(f\) an der Stelle \(x = 6\): \(G_f\) endet im Punkt \((6|2)\) senkrecht auf der gedachten Geraden mit der Gleichung \(y = 2\).
