Teilaufgabe 1d
Lösung zu Teilaufgabe 1d
\[f(x) = \frac{20x}{x^2 - 25}\,; \quad D_{f} = \mathbb R \,\backslash\,\{-5;5\}\]
\[f^{*}(x) = \frac{20x}{x^2 - 25}\,; \quad D_{f^{*}} =\; ]5;+\infty[\]
Begründung, weshalb die Funktion \(f\) nicht umkehrbar ist, die Funktion \(f^{*}\) dagegen schon
1. Lösungsansatz: Definition einer Funktion
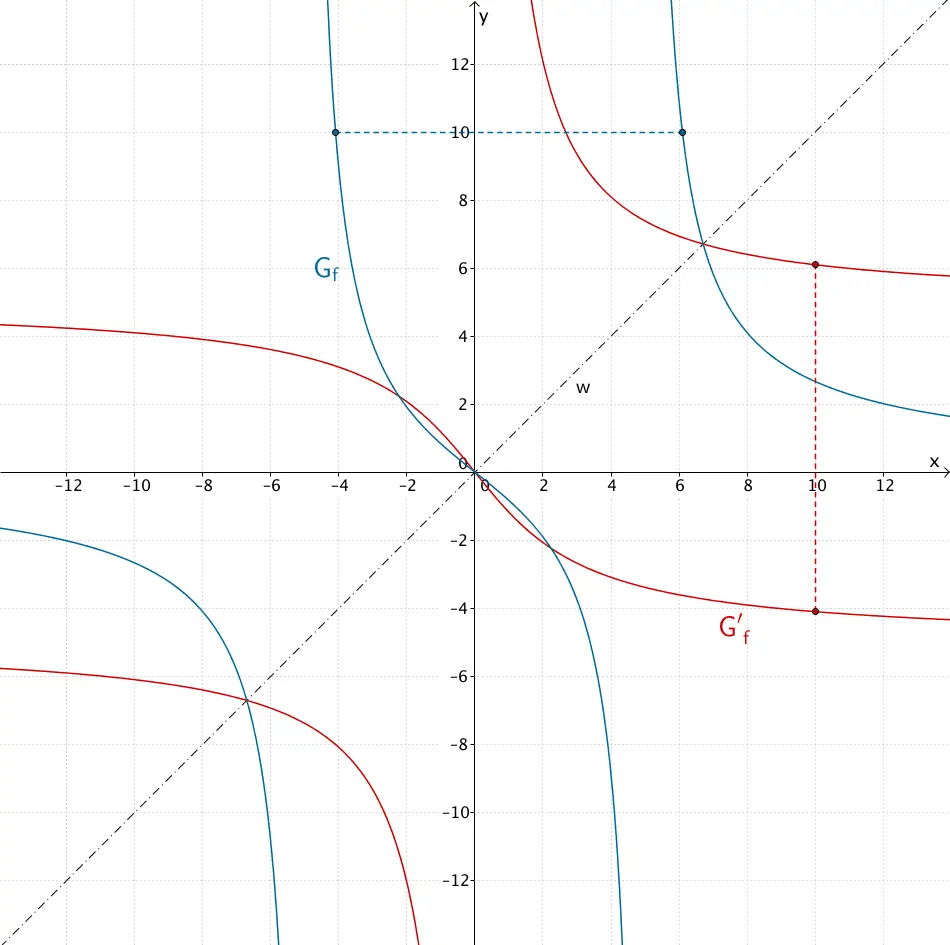
Graph der Funktion \(f\) und dessen an der Winkelhalbierenden \(w\) gespiegeltes Bild \(G'_{f}\)
Die Funktion \(f\) ist in \(D_{f}\) nicht umkehrbar, da es - mit Ausnahme von \(y = 0\) - zu jedem \(y \in W_{f}\) zwei \(x \in D_{f}\) gibt. Spiegelt man \(G_{f}\) an der Winkelhalbierenden \(w\), so lässt sich das Spiegelbild \(G'_{f}\) nicht mit einer Funktion beschreiben, da nicht jedem \(x \in D_{f}\) jeweils eindeutig ein \(y \in W_{f}\) zugeordnet werden kann.
Der Funktion \(f^{*}\) mit dem eingeschränkten Definitionsbereich \(D_{f^{*}} = ]5;+\infty[\) ist umkehrbar, da es zu jedem \(y \in W_{f^{*}}\) jeweils genau ein \(x \in D_{f^{*}}\) gibt.
2. Lösungsansatz: Monotonieverhalten
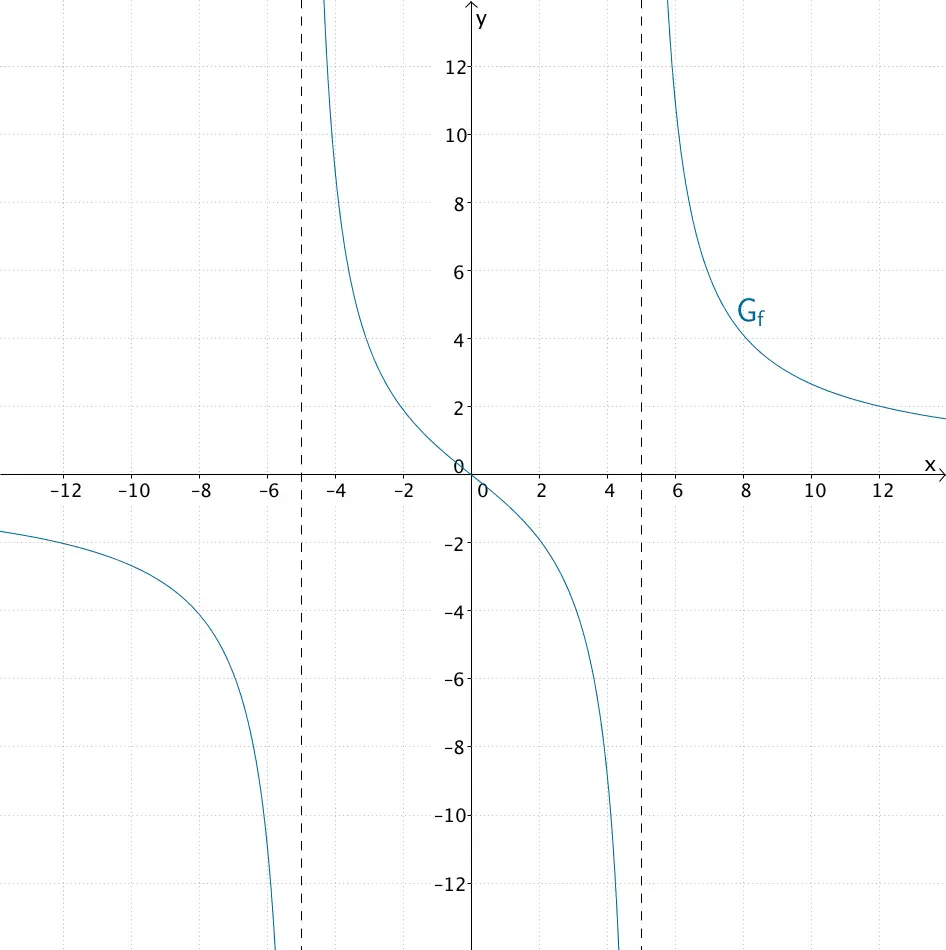
Graph dr Funktion \(f\)
Die Funktion \(f\) ist in den Intervallen \(]-\infty;-5[\), \(]-5;5[\) und \(]5;+\infty[\) jeweils streng monoton fallend und damit in dem jeweiligen Intervall auch umkehrbar. Sie ist aber aufgrund ihrer Definitionslücken in \(\mathbb R\) nicht streng monoton fallend und somit in \(\mathbb R\) nicht umkehrbar.
Die Funktion \(f^{*}\) mit dem eingeschränkten Definitionsbereich \(D_{f^{*}} = \; ]5;+\infty[\) ist umkehrbar, da sie in \(D_{f^{*}}\) streng monoton fallend ist.
Einzeichnen des Graphen der Umkehrfunktion von \(f^{*}\)
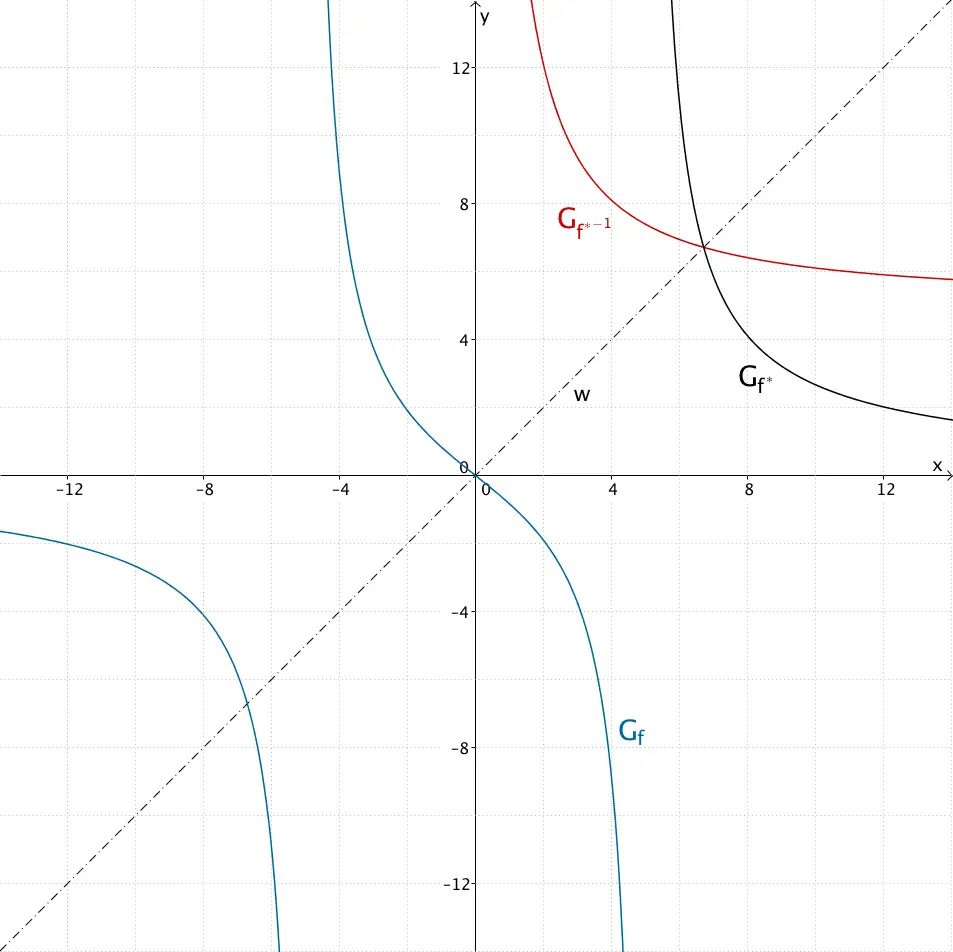
Graph der Funktion \(f\), Graph der Funktion \(f^{*}\) und Graph der Umkehrfunktion \({f^{*}}^{-1}\) von \(f^{*}\)
Der Graph der Umkehrfunktion \({f^{*}}^{-1}\) von \(f^{*}\) entsteht durch Spiegelung des Graphen der Funktion \(f^{*}\) an der Winkelhalbierenden \(w\) des I. und III. Quadranten.
